
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модели и матрица проводимостей биполярного транзистораСодержание книги
Поиск на нашем сайте
В качестве независимых переменных выбираем
Найдём полный дифференциал:
Если работать на линейных участках характеристик транзистора, то:
Запишем (2.1.2) с учётом (2.1.3):
Систему (2.1.4) можно записать, выразив токи. Составляющей
Имея систему (2.1.5) зарисуем модель БТ:
Запишем узловые уравнения за первым законом Кирхгофа для токов узлов с учётом (2.1.5) и (2.1.6). Условимся токи, направленные от узла, считать положительными. Получим уравнение (2.1.7):
Матрица проводимостей:
Также можно записать следующим образом: На (рис 2.1.3) приведена модель БТ на ВЧ ( Модели и матрица проводимостей полевого транзистора
При работе на линейном участке, можно записать:
Перепишем (2.2.2) с учётом (2.2.3):
Крутизна управляющей характеристики при
Проводимость при
Эти параметры определяются по семейству выходных характеристик полевого транзистора. Исходя из (2.2.3) и (2.2.4):
Строим линейную модель на НЧ:
Запишем узловые уравнения за первым законом Кирхгофа для схемы на рис. 2.2.2:
Перепишем (2.2.7) в матричной форме:
Также можно записать следующим образом:
Модели и матрица проводимостей электровакуумного триода
При работе на линейном участке, можно записать:
Перепишем (2.3.2) с учётом (2.3.3):
Модель электровакуумного триода:
Узловые напряжения аналогичны.
Запишем узловые уравнения для этой схемы (рис. 2.3.2) без учёта ёмкостей. Запишем (2.3.4) с учётом (2.3.5):
Перепишем (2.3.6) в матричной форме:
Также можно записать следующим образом:
Алгоритм составления матриц проводимостей схемы, содержащей Источник Тока Управляемый Напряжением (ИТУН) Обозначить узлы схемы буквами или цифрами; Определить порядок матрицы проводимостей по числу узлов без учёта нулевого; На пересечении строк и столбцов с одинаковыми обозначениями (т.е. главную диагональ матрицы проводимостей). Примем собственную проводимость узлов со знаком «+». На пересечении строк и столбцов с разными обозначениями вписуем взаимную проводимость со знаком минус.
В матрицу проводимостей впишем управляющий параметр ИТУН.
Пример:
На пересечении определённых строк и столбцов надо вписать УП вписывается в ячейку матрицы со знаком «+», если ИТУН направлен по отношению к узлу, определяющему номер строки, противоположно направлению УН по отношению к узлу, определяющему номер столбца. Иначе – со знаком минус. Составим матрицу проводимостей рис. 2.3.2 на ВЧ. Всего узлов – 4, без учёта нулевого – 3.
c a к
Модели и матрица проводимостей схемы операционного усилителя
Схема операционного усилителя представлена на рис. 2.5.1. И – инвертирующий вход, Н – не инвертирующий ход, В – выходной зажим. Макромодель ИОУ (рис. 2.5.2): Коэффициент усиления: Y=
Модели и матрица проводимостей индуктивно связанных котушек Запишем уравнения по второму закону Кирхгофа:
Перепишем (2.6.1) в матричной форме:
Также можно записать следующим образом:
Запишем (2.6.4) в виде:
Запишем (2.6.5) в алгебраической форме:
Имея (2.6.6) составим модель: Алгоритм составления матрицы проводимостей схемы без представления компонентов схемы моделью Рассмотрим алгоритм на примере: Выпишем матрицу полевого и биполярного транзисторов, ОУ:
Суммарная матрица проводимости имеет вид:
Пример 2. Схему (рис. 2.) представим моделями с ИТУН: рис. 2.
В матрицу проводимости вписываем управляющие параметры ИТУН.
Составим матрицу проводимостей:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 705; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.26.44 (0.009 с.) |

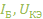 :
:



 можно пренебречь. Получим:
можно пренебречь. Получим:




 .
.
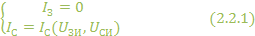





 :
:


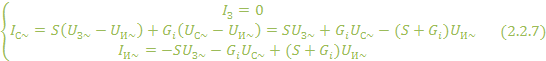

 .
.






 .
. – ИТУН,
– ИТУН,  - УН;
- УН;  – УП.
– УП. Номера строк определяются номерами узлов между которыми лежит ИТУН. А номера столбцов – номерами узлов, между которыми лежит УН.
Номера строк определяются номерами узлов между которыми лежит ИТУН. А номера столбцов – номерами узлов, между которыми лежит УН.




 Составим матрицу проводимостей для ИОУ:
Составим матрицу проводимостей для ИОУ:
 Uин
Uин



 .
.

 ;
;


 =
=



















 Uэк
Uэк



