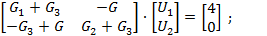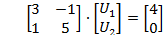Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация обратных связейСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
По способу снятия обратной связи различают обратную связь по напряжению (а,б) и по току (б, г). По способу подачи на вход различают обратную связь параллельного типа (а,б) и последовательного типа (в,г).
Рис 7.1.1
Обратная связь бывает положительной (ПОС) (
Влияние обратной связи на коэффициент передачи по напряжению Рис 7.2.1
Отрицательная обратная связь: Положительная обратная связь:
Влияние обратной связи на нестабильное усиление
Найдём полный дифференциал
Определим соотношение
Запишем
Влияние обратной связи на входное сопротивление Последовательная обратная связь по току Рис 7.4.1 Найдём
Найдём входное сопротивление с обратной связью:
Рис 7.4.2
Составим модель усилителей рис 7.4.3 Рис 7.4.3
Составляя матрицу проводимостей и определив значение
Обратная связь по напряжению параллельного типа
Рис 7.4.4 Найдём
При положительной обратной связи:
Положительная обратная связь как правило в усилителях не применяется, а в генераторах – применяется.
Влияние обратной связи на частоту §7.5.1. Влияние обратной связи на частоту
Рис 7.5.1
§7.5.2. Влияние обратной связи на частоту Рис 7.5.2
Влияние обратной связи на выходное сопротивление Влияние обратной связи по напряжению Рис. 7.6.1. с ИТУН
При холостом ходе
Влияние обратной связи по току Рис 7.6.3
Численные методы анализа электронных схем с нелинейными компонентами Метод простых итераций Любую электронную схему в области средних частот можно представить макромоделью (рис. 8.1).
Запишем уравнения
Запишем уравнения
Рис 8.1.1
Алгоритм решения уравнения методом простых итераций:
Выбираем начальное приближение
Вычисляем
Вычисляем
Продолжаем выполнять эти действия пока не выполнится условие в п.3.
Пример: Определить токи и напряжения, статическое и динамическое сопротивление на нелинейном элементе методом простых итераций в схеме (рис.8.1, а) если известно:
Составим таблицу:
Найденный ток
Определяем напряжения на компонентах схемы:
Определим статическое и динамическое сопротивление:
Данный метод имеет недостатки:
Относительно большое количество итераций;
Иногда низкая сходимость результатов.
Метод Ньютона – Рапсона
Запишем функцию
Алгоритм аналогичен методу простых итераций.
Тема 9. Чувствительность электронной схемы к вариации параметров Чувствительность и нормализованная чувствительность функций схем к вариации первичных параметров Под действием дестабилизирующих факторов (изменение температуры, влажности, давления, радиации, старения компонентов) изменяются первичные параметры компонентов схемы, а значит, и вторичные параметры также изменяются.
Более полное представление даёт относительная величина:
Пример: Определить чувствительность передаточной функции к вариации параметров, нормализованную чувствительность передаточной функции, а также абсолютное и относительное изменение передаточной функции при изменении первичных параметров на 10%.
рис.1
Составим матрицу проводимостей:
Ku=
Ku(q)=Ku(h11, h21, h22, G2);
Найдем абсолютное изменение передаточной функции к вариации первичных параметров.
Найдем нормализованную чувствительность функции к вариации первичных параметров.
Чувствительность узловых напряжений при вариации первичных параметров
Уравнения узловой модели:
Найдём производную:
Где
Пример: Определить чувствительность узловых напряжений к вариации параметров схемы.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 421; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.144.239 (0.011 с.) |

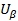 совпадает по фазе с
совпадает по фазе с 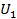 ) и отрицательной обратной связью (
) и отрицательной обратной связью (
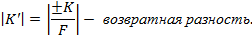
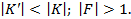
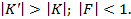

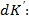
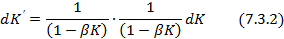
 :
: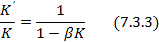
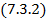 с учётом
с учётом 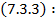
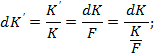
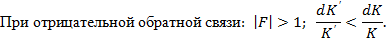
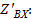
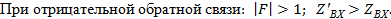
 Определив значение
Определив значение 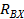 , приняв
, приняв 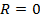 окажется, что
окажется, что 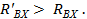
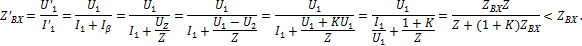
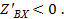
 усилителя
усилителя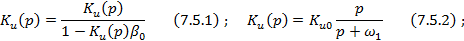
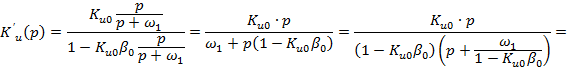

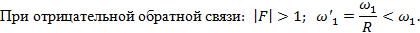
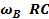 усилителя
усилителя
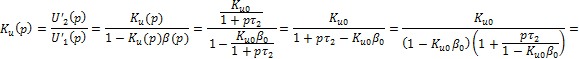

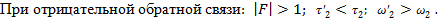
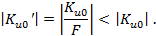
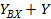
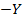


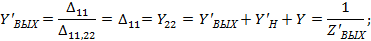
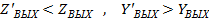
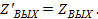
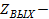 выходное сопротивление при действии отрицательной обратной связи.
выходное сопротивление при действии отрицательной обратной связи.
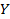 =
=

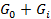
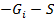
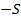
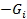
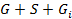
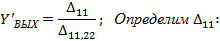
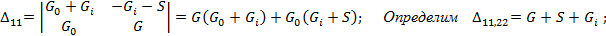

 го закона Кирхгофа для схемы а):
го закона Кирхгофа для схемы а):

 го закона Кирхгофа для схемы б):
го закона Кирхгофа для схемы б):


 ;
; и проверяем разность;
и проверяем разность; ;
; и проверяем разность;
и проверяем разность;
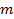



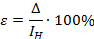
















 равен:
равен:  .
.
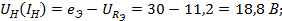



 в окрестности точки
в окрестности точки  . Разложим в ряд Тейлора
. Разложим в ряд Тейлора







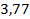



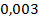
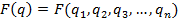 . Под действием дестабилизирующих факторов функции изменяются:
. Под действием дестабилизирующих факторов функции изменяются:
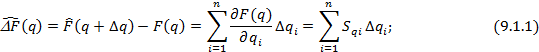
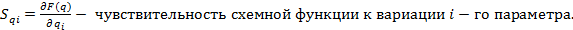 (9.1.2)
(9.1.2)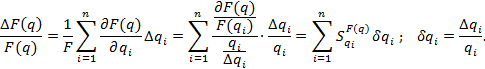
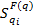 – нормализированная чувствительность;
– нормализированная чувствительность;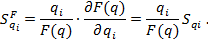




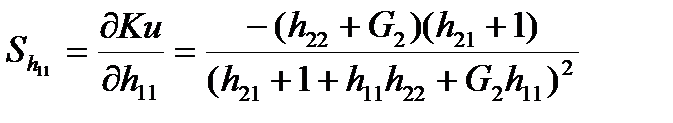
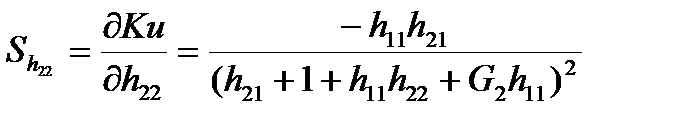

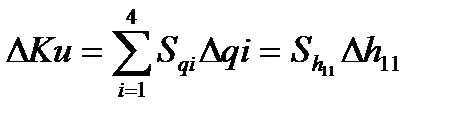 +
+  +
+  +
+ 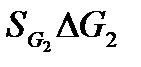
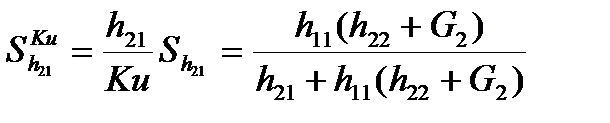
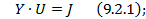

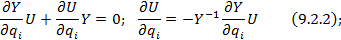
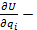 чувствительность узловых напряжений к изменению первичных параметров.
чувствительность узловых напряжений к изменению первичных параметров.