
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практика 4. Обратная матрица.Содержание книги Поиск на нашем сайте
Формула вычисления элементов обратной матрицы: Алгоритм нахождения 1. Проверить невырожденность с помощью определителя. 2. Составить матрицу из дополняющих миноров Mij. 3. Изменить знаки в шахматном порядке, то есть домножить на (-1)i+j, где i,j - номера строки и столбца. 4. Транспонировать полученную матрицу. 5. Поделить на определитель исходной матрицы. Задача 1. Найти обратную матрицу для Решение. 1). Проверяем определитель 2) Составляем матрицу из дополняющих миноров, то есть для каждой клетки вычёркиваем строку и столбец, остаётся подматрица порядка 1, то есть то число, которое напротив, как раз и является дополняющим минором. Получаем 3) В шахматном порядке меняем знак там, где i+j нечётное. Тем самым, мы переходим от 4) Транспонируем эту матрицу. 5) Определитель был равен 1. Делить на 1 не обязательно, можно автоматически считать, что уже и так разделили. В качестве домашнего задания сделать проверку, и потренироваться умножать матрицы.
Матричные уравнения. Пусть А - квадратная матрица
Задача 2. Решить матричное уравнение Решение. Требуетсянайти Так, можно использовать
Ответ.
Задача 3. Решить матричное уравнение Решение. Сначала найдём обратную матрицу
Матрица из алг. дополнений: Транспонируем её: Делим её на определитель, и получаем
Ответ. Задача 4. Найти обратную матрицу Решение. Сначала ищем определитель. Так как матрица треугольная, то достаточно перемножить числа по диагонали. Строим матрицу, состоящую из дополняющих миноров. Зачёркиваем ту строку и тот столбец, где находится элемент, и остаётся минор 2 порядка из 4 элементов. На схеме показано, что именно надо зачеркнуть:
Теперь надо сменить знаки в шахматном порядке, т.е. переходим от миноров к алгебраическим дополнениям. Обведено красным, где надо менять знак. Ясно, что 0 остаётся 0, там знак менять нет смысла.
Получили: Транспонируем эту матрицу, то есть бывшие строки запишем по столбцам.
Ответ. Задача 5. Найти обратную матрицу Решение. Найдём определитель
Найдём матрицу из дополняющих миноров к каждой из 9 клеток.
Меняем знаки в шахматном порядке, то есть там, где i+j нечётное.
Затем транспонируем эту матрицу.
Ответ. Задача 6. Найти обратную матрицу Решение. Сначала находим определитель.
Найдём матрицу из дополняющих миноров.
Меняем знаки в шахматном порядке, там, где i+j нечётное.
Затем транспонируем эту матрицу.
Ответ. Задача 7. Матричным методом решить систему уравнений:
Решение. Запишем систему в виде: Обратите внимение, что основная матрица системы это та самая матрица, для которой мы нашли обратную в прошлой задаче. Если у нас есть равенство
Ответ. Задача 8. Найти обратную матрицу Решение. Сначала вычислим определитель:
Исходный определитель был равен 1, так что делить не нужно. Ответ. Задача 9. Теоретическое упражнение на тему «единственность обратной матрицы». Доказать, чтоне существует различных обратной слева и справа, то есть, если Решение. Пусть Но тогда получается Задача 10. Найти обратную матрицу Решение. Найдём определитель:
Осталось разделить на Ответ.
Практика 5. Ранг матрицы. Задача 1. Найти ранг матрицы. Решение. Метод 1. Выбираем окаймляющие миноры, начиная от левого верхнего угла. Видно, что минор 2 порядка не равен 0, поэтому ранг больше или равен 2. Вычисляя минор 3 порядка (а он здесь единственный, это и есть сам определитель матрицы) видим, что он равен 0.
Метод 2. Преобразуем матрицу к треугольному виду. Вычитаем из 2-й строки 1-ю, и из 3-й удвоенную 1-ю.
Теперь 2-ю строку, умноженную на 0,5, прибавим к 3-й.
Теперь видно, что 3-я строка состоит из нулей, поэтому ранг не может быть равен 3. Минор 2-го порядка тоже сразу виден, это
Ответ.
Задача 2. Найти ранг матрицы Решение. Поменяем 1-ю и 2-ю строки, так чтобы в верхнем левом углу было число 1. Это удобнее для преобразований к треугольной форме методом Гаусса. Ранг при этом не меняется. После этого, вычтем 1-ю строку с коэффициентом 1 либо 4 из последующих, так, чтобы обнулить всё ниде углового элемента.
Ещё мы поменяли 2 и 3 строку, чтобы продолжить метод Гаусса без излишних дробных коэффициентов. Теперь 2-ю строку, домноженную на 10, прибавим к 3-й.
Итак, исходная матрица сводится к такой, в которой уже есть треугольная сруктура в первых трёх столбцах.
Очевидно, что обведённый минор равен 46, не равен 0. Он 3-го порядка, поэтому ранг равен 3. Ответ: Задача 3. Найти ранг матрицы и базисный минор. Решение. Преобразуем матрицу:
Сначала из 2 строки вычитаем 1-ю, домноженную на 2, то есть вычитаем строку (2 4 6) а из 3-й 1-ю, домноженную на 5, т.е. строку (5 10 15). Затем к 3-й прибавляем 20ю с коэффициентом 7. Видно, что базисный минор не может быть в левом верхнем углу, потому что во 2-й строке два нуля. Зато можно найти минор 2 порядка, состоящий из частей 10и 3 столбца, либо 2 и 3-го.
Минор порядка 3, то есть сам определитель всей этой матрицы, равен 0, так как третий столбец содержит только нули. Поэтому ранг равен 2, а не 3. Ответ. Задача 4. Найти ранг матрицы Решение. Преобразуем матрицу. Ко второй строке прибавим 1-ю, а от 3-й отнимем удвоенную 1-ю. теперь к третьей прибавим вторую, получим Ранг равен 3, так как есть невырожденный минор 3 порядка. Ответ.
Задача 4а (вариант с параметром). Найти параметр равен 2.
Третья строка сосотяла бы из всех нулей, только если Ответ. Задача 5. Доказать, что 3 столбец матрицы
является линейной комбинацией первых двух, и найти коэффициенты этой комбинации. Решение. Во-первых, если вычислить определитель и обнаружить, что он равен 0, то этим самым уже доказана линейная зависимость столбцов. Однако требуется найти коэффициенты, поэтому запишем систему уравнений:
Прибавим удвоенное 1-е уравнение ко 2-му, и вычтем утроенное 1-е из 3-го.
Ответ. коэффициенты линейной комбинации равны 1 и 2. Задача 6. Найти ранг матрицы Решение. Преобразуем методом Гаусса к треугольной форме.
Видно, что 4-я строка из нулей, поэтому ранг не равен 4, то есть
Этот минор невырожденный, и он тоже является окаймляющим (ведь он полностью включает в себя квадрат, закрашенный жёлтым). Мы нашли базисный минор порядка 3. Также можно было рассматривать аналогичное в 1,2,5 столбцах, тоже минор порядка 3. Ответ.
Задача 7. Найти такие параметры
Решение. Преобразуем методом Гаусса к треугольной форме.
Если Ответ.
Задача 8. Найти ранг матрицы (4*4, можно с произвольными элементами, заданными группой).
Решение. Для удобства преобразования методом Гаусса, сначала поменяем местами 1 и 3 строки. Ещё можно сразу прибавить 3-ю строку к 4-й.
Дальше стандартным методом, обнулим всё ниже угла.
Для удобства вычислений домножим 2 строку на (-1), ранг при этом не меняется. Затем прибавим к 3 строке удвоенную 2-ю.
Теперь осталось прибавить к 4 строке удвоенную 3-ю.
Ответ.
Элементы векторной алгебры. Задача 9. (8.16 [1]) Найти косинус угла между векторами Решение. Известно, что
Ответ. cos = 9/19.
Задача 10. Найти скалярное и векторное произведение векторов:
Решение. Для поиска векторого произведения запишем определитель.
Ответ. Скалярное: 16, векторное: (-13, -1, -8).
Задача 11. Дано: Решение. Примечание. Как видим, можно вычислять скалярное произведение, даже не зная коорднат векторов. Здесь фактически Ответ.
|
|||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 279; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.209.71 (0.011 с.) |

 .
. .
. .
. , так что обратная матрица существует.
, так что обратная матрица существует. .
. к
к  . Получили
. Получили  .
. .
.
 .
. ,
,  - матрицы размера
- матрицы размера  (чаще всего в таких задачах
(чаще всего в таких задачах  , то есть все рассматриваемые матрицы квадратные), причём
, то есть все рассматриваемые матрицы квадратные), причём  - неизвестная матрица. Тогда определено умножение
- неизвестная матрица. Тогда определено умножение  . Матрицу
. Матрицу  . Тогда
. Тогда  , то есть
, то есть  .
. .
.
 =
=  .
. .
.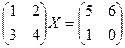 .
. . Матрица из миноров:
. Матрица из миноров:  .
. .
. .
. .
. =
=  .
. .
. .
.
 =
=  =
=  .
.
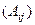 =
= 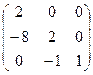 .
. =
=  . И осталось разделить на
. И осталось разделить на  .
. .
.
 .
. =
=  .
. .
. . Осталось только разделить на
. Осталось только разделить на  .
. .
. .
.
 .
. =
=  .
. .
. . Затем делим на
. Затем делим на  .
. =
=  .
.

 .
. , то
, то  , тогда
, тогда  .
. =
=  =
=  .
. =1,
=1,  =1,
=1,  =0.
=0. .
. .
. =
= 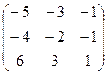 .
. ,
,  .
. и
и  , то
, то  .
. .
. , то есть
, то есть  .
. .
.
 =
=  .
. ,
,  .
. .
. .
. .
.
 .
. . Тогда раен не равен 3.
. Тогда раен не равен 3. , но при этом
, но при этом  . Остаётся единственный вариант:
. Остаётся единственный вариант:  .
.



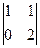
 .
.


 .
.
 .
. .
.



 .
.
 .
. , при котором ранг матрицы
, при котором ранг матрицы


 , то есть
, то есть  . То есть, если бы на месте a33 изначально было число -2, то ранг был бы меньше, так как в итоге получилась бы третья строка из всех нулей.
. То есть, если бы на месте a33 изначально было число -2, то ранг был бы меньше, так как в итоге получилась бы третья строка из всех нулей.


 отсюда видно, что
отсюда видно, что  , тогда
, тогда  .
.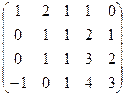 .
.

 .
. . Минор порядка 2 легко находится в верхнем левом углу, но угловой минор порядка 3 равен 0. Однако это ещё не значит, что ранг равен 2, ведь можно отступить к правмому краю матрицы и взять минор с разрывом, из 1,2,4 столбцов, например такой:
. Минор порядка 2 легко находится в верхнем левом углу, но угловой минор порядка 3 равен 0. Однако это ещё не значит, что ранг равен 2, ведь можно отступить к правмому краю матрицы и взять минор с разрывом, из 1,2,4 столбцов, например такой:
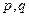 , что ранг матрицы равен 1:
, что ранг матрицы равен 1:
 .
. и
и  , то две последних строки только из нулей, и равен будет равен 1.
, то две последних строки только из нулей, и равен будет равен 1.






 . Видно, что получилась треугольная матрица, то есть определитель 4 порядка невырожденный. Поэтому
. Видно, что получилась треугольная матрица, то есть определитель 4 порядка невырожденный. Поэтому  .
. .
. .
. ,
,  .
. , тогда
, тогда  , что приблизительно равно 0,5, то есть угол чуть больше 600.
, что приблизительно равно 0,5, то есть угол чуть больше 600. и
и  .
. .
. =
=  =
=  .
. ,
,  ,
,  ,
,  , угол между векторами
, угол между векторами  45 градусов. Найти
45 градусов. Найти  .
. =
=  =
= 
 .
. , то есть (1,1) и (2,1) координаты
, то есть (1,1) и (2,1) координаты 


