
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практика 3. (9 сентября у обеих групп).Содержание книги Поиск на нашем сайте Определители, разложение по строке (столбцу). Задача 1. Найти произведение
Решение. Вычислим
Замечание. Если вычислять
Замечание. При умножении квадратной матрицы на вектор-столбец получается снова вектор-столбец, то есть квадратная матрица фактически выступает в роли функции, отображающей векторы в пространстве (или на плоскости, если n = 2).
Задача 2. Умножение квадратной матрицы порядка 3 на вектор-столбец из 3 координат (параметры произвольные, задаёт группа). Задача 3. Найти параметр
Решение. Вычислим определитель и решим получившееся уравнение:
Ответ. Задача 4. Найти объём тетраэдра, вершины которого A(1,1,1), B(2,1,3), C(2,2,4), D(1,2,4). Решение. Объём тетраэдра ровно в 6 раз меньше объёма параллелепипеда с рёбрами AB, AC, AD. Найдём эти векторы, и сначала вычислим объём параллелепипеда с помощью определителя, затем поделим на 6. AB = (1,0,2), AC = (0,1,3), AD = (1,1,3).
Ответ. Объём тетраэдра равен Задача 5. Вычислить определитель Решение. Выберем дополняющий минор для каждого элемента 1-й строки, и домножим на
Задача 6. Вычислить определитель Решение. Вычитаем из 2-й строки удвоенную 1-ю, и из 3-й 1-ю.
получили Задача 7(а,б). Вычислить определитель 4 порядка двумя способами: а) разложением по 1-й строке. б) с помощью преобразований матрицы, т.е. приведением к треугольной форме.
Решение. Первый способ. Разложение по 1-й строке:
Очевидно, что последние 2 минора 3-го порядка вычислять не надо, так как они умножаются на 0. Осталось вычислить два минора 3 порядка, то есть мы свели определитель 4 порядка к определителям 3 порядка.
Ответ. 0. Второй способ. Из 2-й строки вычтем удвоенную 1-ю, а из 4-й утроенную 1-ю.
Здесь мы добиваемся того, чтобы под левым верхним углом были только нули. В 3-й строке слева и так 0, из неё ничего вычитать не надо. Теперь к 3-й строке прибавим 2-ю, а из 4-й вычтем удвоенную 2-ю. Этим самым мы обнулим элементы ниже
Теперь надо к 4-й строке прибавить 3-ю, и мы получим 0 под элементом
Но получилось так, что вся 4 строка состоит из нулей, а тогда определитель равен 0. Итак, получили точно такой же ответ. Задача 8. Вычислить определитель Решение. Здесь можно применить старый, давно известный способ, то есть достроить 2 столбца и перемножить по трём параллельным линиям. А можно и преобразования строк. Но для этого удобно, чтобы в левом верхнем углу было число 1. Мы можем поменять местами строки, учтём, что при этом сменится знак.
В принципе, можно ещё и поменять местами 2 и 3 строки, чтобы знак снова исчез.
Задача 9. Вычислить определитель Решение. Прибавим 1-ю строку ко 2-й, 3-й и 4-й.
Ответ. 24. Задача 10. Вычислить определитель Решение. Можно просто добавить копии 1,2 столбцов и применить старый способ, а можно разложить по 3 строке, где есть всего одно ненулевое число. Сделаем именно так.
Ответ. 28. Задача 11. Вычислить определитель Решение. Приведём к треугольному виду.
|
||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 314; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.009 с.) |

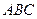 , где
, где ,
, 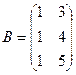 ,
,  .
. , сначала умножим первые две матрицы:
, сначала умножим первые две матрицы:
 =
=  . Теперь умножим на третью матрицу.
. Теперь умножим на третью матрицу. =
= 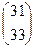 . Ответ.
. Ответ.  , то получается точно такой же результат, т.к. выполняется закон ассоциативности.
, то получается точно такой же результат, т.к. выполняется закон ассоциативности. , при котором определитель равен 0:
, при котором определитель равен 0: .
. ,
,  ,
,  ,
,  .
. =
= 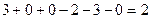 ,
,  .
. .
. с помощью разложения по первой строке.
с помощью разложения по первой строке.
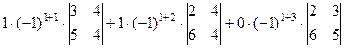 =
= =
=  = 8. Ответ. 8.
= 8. Ответ. 8. методом Гаусса (приведением к треугольной форме).
методом Гаусса (приведением к треугольной форме). затем вычитаем из 3-й строки 2-ю.
затем вычитаем из 3-й строки 2-ю. = 2. Ответ. 2.
= 2. Ответ. 2.

 =
=  .
.
 .
.
 , этим как раз и завершится процесс приведения к треугольному виду.
, этим как раз и завершится процесс приведения к треугольному виду.
 .
. .
. . А вот теперь уже вычитать из 2-й строки (удвоеннную 1-ю) и из 3-й (утроенную 1-ю).
. А вот теперь уже вычитать из 2-й строки (удвоеннную 1-ю) и из 3-й (утроенную 1-ю).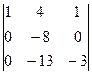 . Дальше можно и не преобразовывать, а просто разложить по 1 стролбцу, там всего лишь одно число, остальные нули.
. Дальше можно и не преобразовывать, а просто разложить по 1 стролбцу, там всего лишь одно число, остальные нули.  = 24. Ответ. 24.
= 24. Ответ. 24. .
. . Эта матрица треугольная, определитель равен произведению чисел по диагонали, то есть 24.
. Эта матрица треугольная, определитель равен произведению чисел по диагонали, то есть 24. .
. =
= 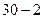 = 28.
= 28.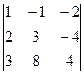 .
. теперь разложим по 1-му столбцу
теперь разложим по 1-му столбцу = 50. Ответ. 50.
= 50. Ответ. 50.


