
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практика 12 (21 октября у обеих групп).Содержание книги Поиск на нашем сайте
Задача 1. Найти расстояние от точки M0 (1,3,5) до плоскости Решение. По формуле
Это значит, что точка принадлежит плоскости. Ответ. Задача 1а. Найти расстояние от точки M0 (7,15,22) до плоскости Решение. По формуле
Ответ. Задача 2. (На плоскости). Даны точки Вывести уравнение прямой, содержащей А1В1, и найти расстояние от точки С1 до этой прямой (то есть высоту треугольника). Решение. Вектор А1В1 равен Теперь по формуле
Ответ. Прямая Задача 3. Найти угол между двумя плоскостями: Решение. Нормали к этим плоскостям: Нормали не коллинеарны, то есть плоскости не параллельны, значит, они действительно пересекаются по какой-то прямой, и между ними есть какой-то угол.
Кстати, константа в уравнении одной из плоскостей никак не влияет на ответ, так как параллельный перенос плоскости не влияет на угол, который она образует с другой плоскостью. Ответ. Прямая в пространстве Задача 4. Построить уравнение прямой в пространстве (каноническое, параметрическое) по точке Решение. Если отложить вектор от
(это мы сейчас получили канонические уравнения). Обратите внимание, что в знаменателях здесь оказались именно координаты направляющего вектора! Чертёж:
Как мы видим, прямая в пространстве задаётся не одним уравнением, а системой уравнений. Здесь как минимум 2 знака равенства. 1-я дробь равна 2-й, а 2-я равна 3-й. На самом деле здесь даже 3 уравнения, ведь ещё и 1-я равна 3-й. Если теперь каждую такую дробь приравнять к некоторому параметру
Тогда Можно их записать ещё и в векторной форме: Они задают движение точки по этой прямой во времени. Здесь при Ответ. Задача 5. Построить уравнение прямой в пространстве (каноническое, параметрическое) по точке и направляющему (с произвольными случайно взятыми параметтрами, которые придумает группа).
Задача 6. Построить уравнение прямой, лежащей в пересечении двух плоскостей Решение. Векторное произведение нормалей
Итак, направляющий вектор Теперь нужно найти хотя бы одну точку на этой прямой. Чтобы взять произвольную точку из пересечения плоскостей, можно положить Два уравнения, без Выразим из 2-го Получим Но тогда Вектор от этой точки к произвольной точке
Приравнивая все эти дроби к Ответ. Задача 7. Доказать, что прямая Решение. Если прямая пересекает ось Если бы первые две дроби после такой подстановки оказались не равны, то это бы означало, что нет пересечения с осью Ответ. (0,0,1). Задача 8. Найти угол между прямой и плоскостью Решение. Формула, выведенная в лекциях: Направляющий к прямой Их скалярное произведение равно 9. Модули векторов равны Приблизительно представим, какой это угол. Если бы было
Но в данном случае дробь чуть меньше, а угол составляет около 79 градусов. Ответ.
Задача 9. Найти параметрические и канонические уравнения прямой, перпендикулярной к плоскости треугольника с вершинами Решение. Направляющие АВ и АС это (3,3,0) и
Их векторное произведение:
Итак, вектор
Ответ. Канонические параметрические
Задача 10. Доказать, что две прямые в пространстве
Решение. Если у них естьь общая точка, то можно приравнять
Преобразуем методом Гаусса. От 2-й строки отнимем утроенную 1-ю, а к 3-й прибавим 4-кратную 1-ю.
Затем подставить получим одни и те же значения для
Ответ точка пересечения (1,1,2). Задача 11. Доказать, что две прямые в пространстве:
Решение. Решая систему уравнений, как в прошлой задаче, здесь мы обнаружим, что система несовместна.
прибавим ко 2-й строке 1-ю, а от 3-й отнимем 1-ю.
2-е и 3-е уравнения противоречат друг другу. Система не имеет решений, значит, эти 2 прямые не имеют ни одной общей точки. Так как направляющие векторы Найдём расстояние между ними. Точку на каждой прямой можно найти, присваивая Вычисляем по формуле Смешанное произведение с помощью определителя.
=
Модуль векторного произведения равен
Дом. задача 1. (12.22 [1]) Доказать, что прямые
Ответ. (3,7,-6). Дом. задача 2. (12.35 [1]) Вычислить расстояние между скрещивающимися прямыми:
Ответ 13. Практика 13. Прямая в пространстве. Кривые и поверхности.
Задача 1. Вычислить расстояние от точки (4,4,-2) до прямой Решение. Применим формулу Точка
Его модуль равен
Модуль этого вектора равен Задача 2. Даны три точки А(1,1,1),В(2,2,3),С(2,1,2). Вывести уравнение прямой, содержащей АВ, и найти расстояние от точки С до этой прямой (высота треугольника АВС). Решение. Вектор АВ (1,1,2) можем принять в качестве направляющего для этой прямой. Он отложен от точки А(1,1,1). Тогда канонические уравнения прямой:
Расстояние в данной ситуации, в пространстве, надо искать по формуле Здесь точки А,С играют ту же роль, что 2-я сторона параллелограмма: АС=(1,0,1). Векторное произведение:
Модуль вектора Ответ. Задача 3. Найти точку пересечения плоскости Решение. Запишем прямую с помощью параметрических уравнений:
Подставим эти выражения в уравнение плоскости, чтобы найти, при каком значении
Ответ. Точка пересечения Задача 4. Через точку Решение. Если плоскость содержит ось и точку, то в ней по крайней мере содержится начало координат, и 2 такие направляющих: один проведён от (0,0,0) к точке А затем мы найдём угол между их нормалями. Эти плоскости можно представить так: две наклонные части крыши. Плоскость, перпендикулярная линии ОМ, не горизонтальна, так что угол между двумя частями такой крыши вовсе не 90 градусов. Чем более пологая крыша, тем ближе этот угол к 180, а чем более крутая, тем ближе к 90. Плоскость, перпендикулярная стыковочной линии крыши, а именно линии ОМ, показана жёлтым цветом.
Строим уравнение 1-й плоскости. Возьмём 3-й вектор, проведённый к какой-то произвольной точке
Нормаль к этой плоскости Строим уравнение 2-й плоскости. Аналогично, только (0,1,0).
Нормаль к этой плоскости Известно, что Тогда Замечание. Если бы надо было найти косинус наименьшего угла, то есть острого, то должны были бы рассматривать модуль
Вообще же, всегда имеется два угла, Задача 5. Заданы 2 прямые в пространстве, одна - своими параметрическими уравнениями, а другая как пересечение пары плоскостей:
Доказать, что эти прямые параллельны, и найти уравнение плоскости, содержащей их.
Решение. Сначала найдём направляющие векторы этих прямых и докажем, что они коллинеарны. Для 1-й прямой надо просто выбрать коэффициенты при Для 2-й прямой надо искать направляющий как векторное произведение нормалей к двум плоскостям.
Векторы Теперь, чтобы построить уравнение плоскости, нужна какая-то точка и два линейно-независимых направляющих вектора в плоскости. При этом два направляющих для этой пары прямых линейно-зависимы, то есть с помощью них построить уравнение не получится. Один из них можем использовать, а 2-й направляющий в плоскости надо ещё найти. Для этой цели можно взять какой-нибудь вектор, соединяющий пару точек на этих прямых. Точка на 1-й прямой: присвоим
Вторым направляющим вектором в плоскости может служить Итак, есть точка
Ответ. Плоскость Задача 6. Доказать, что кривая является эллипсом, найти каноническое уравнение, центр и полуоси. Решение. Выделим полный квадрат по каждой переменной.
Чертёж:
Ответ. Центр Задача 7. Доказать, что кривая является эллипсом, найти каноническое уравнение, центр и полуоси, построить чертёж. Решение. Здесь в уравнении есть произведение Находим собственные числа и векторы.
Собственные числа 1 и 9. Ищем собственные векторы.
Нормируем его, то есть делим на длину, которая здесь
Это единичный вектор в 1-й четверти, получающийся поворотом (1,0) на 45 градусов.
Нормируем его, получаем Это вектор во 2-й четверти, получающийся поворотом (0,1) на 45 градусов. Запишем формулы перехода от одного базиса к другому:
Если подставить эти выражения в исходное уравнение, то после приведения подобных исчезнут выражения, содержащие разные переменные
в линейной форме
Итак, как мы видим, коэффициентами как раз и оказались 9 и 1, то есть собственные числа матрицы этой квадратичной формы. Заметим, что 1-й степени
Центр
Если Итак, центр - точка (1,1). В направлении первого вектора нового базиса, а именно Ответ. Центр Чертёж:
Задача 8. Доказать, что однополостный гиперболоид Решение. В горизонтальном сечении при
Это пара пересекающихся прямых.
Чертёж: эта пара прямых показана красным цветом.
Домашняя Задача 1. (13.16 [1]). Доказать, что кривая Ответ. Центр (3,-1), полуоси 3 и
Домашняя задача 2. (14.3 а [1]). Доказать, что кривая
Практика 14. Повторение и контрольная работа. Векторы a,b выражены через p,r: Задача 1. Найти Задача 2. Найти | [a,b] |. Ответ. 50. Задача 3. Решить систему уравнений Ответ. Задача 4. Найти собственные числа и векторы Ответ. Собст. число собст. число собст. число
Задача 5. Построить уравнение прямой (на плоскости) по точке Задача 6. Построить уравнение прямой (на плоскости) по точке Задача 7. Построить уравнение плоскости, проходящей через точку А (1,2,3) перпендикулярно вектору Задача 8. Построить уравнение плоскости по точке Задача 9. Построить уравнение прямой в пространстве (каноническое, параметрическое) по точке | ||
|
| Поделиться: |

 .
. получаем, что
получаем, что =
=  =
=  .
. .
. =
=  .
. .
.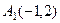 ,
,  ,
,  .
. , и это есть направляющий на прямой. В то же время вектор А1М до произвольной точки
, и это есть направляющий на прямой. В то же время вектор А1М до произвольной точки  , который равен
, который равен  , пропорционален А1В1. Тогда
, пропорционален А1В1. Тогда  , то есть
, то есть  , и уравнение прямой:
, и уравнение прямой:  .
. найдём расстояние от этой прямой до точки
найдём расстояние от этой прямой до точки  =
=  =
=  .
.
 и
и  .
. и
и  .
.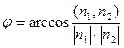 =
=  =
=  .
. , что приблизительно составляет 83,6 градусов.
, что приблизительно составляет 83,6 градусов. и направляющему
и направляющему  .
. , то вектор
, то вектор  коллинеарен вектору
коллинеарен вектору 

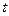 , то:
, то:  ,
,  ,
,  , следовательно:
, следовательно: ,
,  ,
,  .
. - параметрические уравнения.
- параметрические уравнения. .
. мы как раз оказались бы в исходной точке, а при
мы как раз оказались бы в исходной точке, а при  в конце направляющего вектора.
в конце направляющего вектора. и
и  .
. это направляющий вектор, вычислим его.
это направляющий вектор, вычислим его.  =
= =
=  .
. .
. и решить систему, вычислив
и решить систему, вычислив  .
. , приводят к такой системе:
, приводят к такой системе: 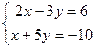 .
. и подставим в 1-е.
и подставим в 1-е. . Тогда
. Тогда  , т.е.
, т.е.  .
. . Итак, получили точку
. Итак, получили точку  .
. равен
равен  и он попорционален направляющему вектору. Тогда
и он попорционален направляющему вектору. Тогда канонические уравнения этой прямой.
канонические уравнения этой прямой. .
. пересекает ось
пересекает ось  и найти точку пересечения.
и найти точку пересечения. . Если в первые две дроби вместо
. Если в первые две дроби вместо  . Тогда
. Тогда 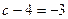 , т.е.
, т.е.  .
.
 .
. .
. , нормаль к плоскости
, нормаль к плоскости 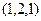 .
. и
и 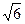 .
.  .
. вместо
вместо  то было бы
то было бы  = 90.
= 90. ,
,  ,
,  и проходящей через вершину А.
и проходящей через вершину А. .
.
 =
= 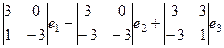 =
=  .
. . Но можно в том же направлении выбрать вектор короче в 3 раза (для удобства вычислений) ведь направление от этого не изменится. Итак, пусть направляющий для прямой
. Но можно в том же направлении выбрать вектор короче в 3 раза (для удобства вычислений) ведь направление от этого не изменится. Итак, пусть направляющий для прямой  , точка
, точка  . Он коллинеарен
. Он коллинеарен  . Это и есть канонические уравнения. Перейти к параметрическим можно так же, как и в прошлых задачах: приравнять все дроби к
. Это и есть канонические уравнения. Перейти к параметрическим можно так же, как и в прошлых задачах: приравнять все дроби к  .
. и
и  пересекаются, и найти точку пересечения.
пересекаются, и найти точку пересечения. из первых и вторых равенств. Но неизвестно, при каком параметре достигаются эти значения в каждом случае, поэтому нужно решить систему уравнений, положив в первых равенствах
из первых и вторых равенств. Но неизвестно, при каком параметре достигаются эти значения в каждом случае, поэтому нужно решить систему уравнений, положив в первых равенствах  , а во вторых
, а во вторых  .
. перенесём все
перенесём все  расширенная матрица:
расширенная матрица: 
 т.е.
т.е.  то есть сразу же
то есть сразу же  из 2-го и 3-го уравнений, и они не противоречат друг другу. Кстати, эта система совместна, равнги основной и расширенной матриц совпадают, так как равны 2. Из 1-го затем
из 2-го и 3-го уравнений, и они не противоречат друг другу. Кстати, эта система совместна, равнги основной и расширенной матриц совпадают, так как равны 2. Из 1-го затем  , т.е.
, т.е.  .
. , т.к.
, т.к.  и
и 
 и
и  скрещивающиеся, и найти расстояние между ними.
скрещивающиеся, и найти расстояние между ними.

 матрица:
матрица: 
 получили систему
получили систему 
 и
и  не коллинеарны, то прямые не параллельные, а скрещивающиеся.
не коллинеарны, то прямые не параллельные, а скрещивающиеся. ,
, 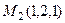 . Вектор, соединяющий две прямых,
. Вектор, соединяющий две прямых,  .
. .
.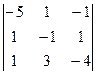 =
=  (прибавили 2-ю строку к 1-й)
(прибавили 2-ю строку к 1-й) =
=  , а по модулю получается 4.
, а по модулю получается 4. =
=  =
=  .
. =
=  .
. . Ответ.
. Ответ.  и
и  пересекаются и найти точку.
пересекаются и найти точку. и
и 
 в пространстве.
в пространстве. .
.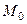 на прямой ищется из таких соображений: все дроби в каноническим уравнении приравняем к 0, тогда
на прямой ищется из таких соображений: все дроби в каноническим уравнении приравняем к 0, тогда 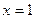 ,
,  ,
,  .
.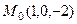 .
.  . Направляющий вектор состоит из чисел в знаменателях в канонических уравнениях:
. Направляющий вектор состоит из чисел в знаменателях в канонических уравнениях:  .
. . Векторное произведение:
. Векторное произведение: =
= 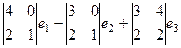 =
=  .
. . Ответ.
. Ответ.  .
. .
.
 .
. в прошлой задаче.
в прошлой задаче. .
. =
=  =
=  .
. равен
равен 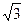 . Тогда результат:
. Тогда результат:  .
. .
.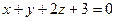 и прямой
и прямой  .
. ,
,  ,
,  .
.

 . Тогда
. Тогда  .
. .
.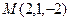 и ось Ох проходит одна плоскость, через эту же точку и ось Оу вторая. Найти косинус тупого угла между этими плоскостями.
и ось Ох проходит одна плоскость, через эту же точку и ось Оу вторая. Найти косинус тупого угла между этими плоскостями. , а второй - это просто базисный вектор оси, то есть для Ох вектор (1,0,0), а в случае оси Оу (0,1,0). Таким образом, уравнения каждой плоскости можно построить.
, а второй - это просто базисный вектор оси, то есть для Ох вектор (1,0,0), а в случае оси Оу (0,1,0). Таким образом, уравнения каждой плоскости можно построить.
 ,
,  =
= 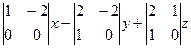 =
=  .
. .
. =
=  =
=  .
. .
. .
. , т.е.
, т.е.  .
. , чтобы угол получился именно в 1-й четверти, т.е. с положительным cos.
, чтобы угол получился именно в 1-й четверти, т.е. с положительным cos.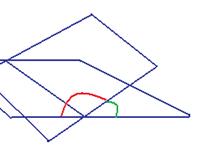
 и
и  . В зависимости от того, острый или тупой угол надо рассматривать, его косинус вычисляется как
. В зависимости от того, острый или тупой угол надо рассматривать, его косинус вычисляется как  либо
либо  . Ответ.
. Ответ. 
 и
и  .
. .
. =
=  =
=  .
.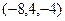 коллинеарны, это видно, если вынести множитель
коллинеарны, это видно, если вынести множитель  . Значит, прямые действительно параллельны.
. Значит, прямые действительно параллельны. . Точку на 2-й прямой можно найти так: в системе из двух уравнений присвоить
. Точку на 2-й прямой можно найти так: в системе из двух уравнений присвоить 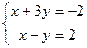



 или
или  , что кстати удобнее, потому что меньше минусов при вычислении (координаты положительны).
, что кстати удобнее, потому что меньше минусов при вычислении (координаты положительны). на плоскости. Построим уравнение плоскости. Третий вектор, проведённый к какой-либо произвольной точке в этой пллоскости, и 2 направляющих, образуют ЛЗС:
на плоскости. Построим уравнение плоскости. Третий вектор, проведённый к какой-либо произвольной точке в этой пллоскости, и 2 направляющих, образуют ЛЗС:

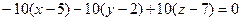
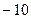
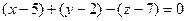
 .
.

 в каждой скобке можно получить такое выражение, чтобы затем использовать формулы сокращённого умножения (ФСУ):
в каждой скобке можно получить такое выражение, чтобы затем использовать формулы сокращённого умножения (ФСУ):  . Надо прибавить константы в скобках, так чтобы всё сворачивалось, но для компенсации за скобками вычесть эти константы.
. Надо прибавить константы в скобках, так чтобы всё сворачивалось, но для компенсации за скобками вычесть эти константы.


 это каноническое уравнение.
это каноническое уравнение.
 , полуоси
, полуоси  и
и  .
.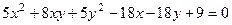
 , то есть надо сначала привести к главным осям квадратичную форму:
, то есть надо сначала привести к главным осям квадратичную форму:  . Строим её матрицу:
. Строим её матрицу:  .
.


 .
. .
.  , оба уравнения пропорциональны, т.е. есть только такая информация:
, оба уравнения пропорциональны, т.е. есть только такая информация: 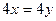 , т.е.
, т.е.  . ФСР: вектор (1,1).
. ФСР: вектор (1,1). . Получаем
. Получаем - собственный вектор для
- собственный вектор для 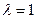 .
.  , оба уравнения пропорциональны, фактически оно одно:
, оба уравнения пропорциональны, фактически оно одно:  , т.е.
, т.е.  . ФСР: вектор
. ФСР: вектор  .
. собственный вектор для
собственный вектор для 

 :
:



 тоже сократятся.
тоже сократятся.

 .
.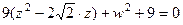
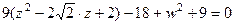

 , т.е.
, т.е.  . Полуоси 1 и 3, то есть размеры эллипса: 2 на 6.
. Полуоси 1 и 3, то есть размеры эллипса: 2 на 6.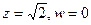 , но это центр в новых координатах, а для чертежа надо найти центр именно в старых координатах
, но это центр в новых координатах, а для чертежа надо найти центр именно в старых координатах  .
.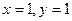 .
.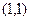 , полуоси 1 и 3.
, полуоси 1 и 3.
 содержит прямолинейные образующие.
содержит прямолинейные образующие.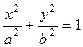 . Его вершины:
. Его вершины:  ,
,  ,
, 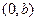 ,
,  . Рассмотрим вертикальную плоскость, проходящую через его вершину, например,
. Рассмотрим вертикальную плоскость, проходящую через его вершину, например,  . Тогда в уравнении гиперболоида
. Тогда в уравнении гиперболоида  , т.е.
, т.е.  . Получается
. Получается 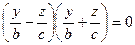 , т.е. в вертикальной плоскости две прямых:
, т.е. в вертикальной плоскости две прямых: и
и  , или можно записать так:
, или можно записать так:  и
и 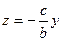 .
.
 является эллипсом, найти каноническое уравнение, центр и полуоси.
является эллипсом, найти каноническое уравнение, центр и полуоси. является эллипсом, найти каноническое уравнение, центр и полуоси, построить чертёж.
является эллипсом, найти каноническое уравнение, центр и полуоси, построить чертёж. ,
,  .
.  , угол между ними 45 град.
, угол между ними 45 град. . Ответ. 29.
. Ответ. 29.

 =2,
=2,  =1,
=1,  =1.
=1.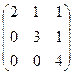 .
. собст. вектор (1,0,0),
собст. вектор (1,0,0), собст. вектор (1,1,0),
собст. вектор (1,1,0), собст. вектор (1,1,1).
собст. вектор (1,1,1). (3,5). Ответ.
(3,5). Ответ.  .
. .
.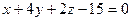 .
. и двум направляющим
и двум направляющим  (4,2,3) и
(4,2,3) и  . Ответ.
. Ответ.  .
.


