
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практика № 6 (23 сентября у обеих групп).Содержание книги Поиск на нашем сайте
45 минут - продолжение темы «скалярное, векторное, смешанное проиведение». Повторение перед контрольной. Задачи 1,2,3. Векторы a,b выражены через p,r: Задача 1. Найти Задача 3. Найти Решение задачи 1.
Это мы раскрыли скобки, используя свойства скалярного произведения. Далее, так как Это можно выразить так:
Решение задачи 2.
Несмотря на то, что скобки мы раскрыли похожим образом, дальше будет существенное отличие, т.к. свойства векторного произведения совсем другие, чем скалярного. Так,
Решение задачи 3.
Задача 4. (8.19 [1]) Вычислить площадь параллелограмма, образованного векторами Решение. Вычислим площадь с помощью векторного произведения.
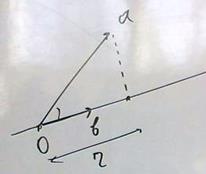
Задача 5. Вывод формулы проекции вектора на ось Во-первых,
(чертёж с доски) Во-вторых, длина проекции
Задача 6. (8.18 [1]) Найти проекцию вектора Решение.
Задача 7. Найти смешанное произведение трёх векторов:
Решение. Вычислим определитель:
Домашнее задание. Векторы a,b выражены через p,q: № 1. Найти
45 минут - контрольная работа. Темы: 1. Умножение матриц 2. Определитель (3-го порядка). 3. Обратная матрица (3-го порядка). 4. Ранг матрицы. Практика № 7 (Подробный разбор домашних задач по скалярному и векторному произведению). Задача 1. Векторы a,b выражены через p,q: Решение.
Ответ. 1227.
Задача 2. Векторы a,b выражены через p,q: Решение. | [a,b] | =
Ответ.
Системы линейных алгебраических уравнений. Сначала решим задачи с помощью матричного метода и с помощью метода Крамера. Задача 3. Решить систему линейных уравнений:
Решение. А. Матричным методом. Запишем систему в виде: Домножим на обратную матрицу слева обе части равенства, для этого сначала найдём обратную матрицу.
Выполним действия, необходимые для поиска обратной матрицы
Умножим
Итак, получили Б. Методом Крамера.
Ответ. Задача 4. Решить систему линейных уравнений:
Решение. А. Матричным методом. Запишем систему в виде: Найдём обратную матрицу для А.
Б. Методом Крамера.
Ответ. Метод Гаусса. Задача 5. Решить систему уравнений Решение. Построим расширенную матрицу системы и преобразуем её.
чтобы обнулились коэффициенты ниже левого верхнего угла, то есть чтобы исчезла переменная а) из 2-й строки вычесть 1-ю; б) из 3-й строки вычест удвоенную 1-ю.
Теперь, чтобы обнулить ниже чем
Когда в основной матрице уже получена треугольная структура, снова перепишем в виде системы
А теперь уже две последних неизвестных стали известны, и с этой информацией поднимаемся в 1-е уравнение, подставляя туда Ответ. Можно ответ записать и в виде вектора:
Задача 6. Решить систему уравнений Решение. Во-первых, можно всё 2-е уравнение сократить на 2, так удобнее для решения, числа будут меньше. Затем обнуляем ниже углового элемента: вычитаем из 2-го уравнения удвоенное 1-е, а также 3-го 1-е.
Перепишем снова в виде системы:
А из 1-го Ответ. Задача 7. Решить систему уравнений Решение. При построении расширенной матрицы, сразу же домножим 2-е и 3-е уравнения на такие коэффициенты, чтобы в начале строки были числа, кратные угловому элементу. А именно, 2-ю строку на 2, а 3-ю строку на 4. Так надо, чтобы потом в методе Гаусса можно было не домножать на дробные коэффициенты при вычитании строк.
Теперь вычтем из 2-й строки 1-ю, домноженную на 3, а из 3-й строки 1-ю, домноженную на 5.
Если теперь поменять местами 2 и 3 строки, получится:
И хотя матрица не выглядит как матрица треугольного вида, тем не менее, основная идея метода Гаусса уже реализована: чем ниже, тем меньше переменных, а в последнем уравнении всего одна, а именно Итак, из третьего: Подставляем во второе уравнение. Из первого: Ответ.
Координаты в новом базисе. Любой вектор можно выразить не только как комбинацию базисных векторов, расположенных на осях, например (1,0) и (0,1), но и как комбинацию какой-то другой линейно-независимой системы. Так, В декартовом базисе координаты (3,2) (пройти 3 шага вправо и 2 вверх), а в новом базисе, состоящем из векторов (1,1) и (1,0) координаты (2,1) (пройти 2 шага по диагонали и 1 шаг вправо).
Найти новые координаты можно так. Запишем их сначала как неизвестные в векторном равенстве:
Матрица, где векторы нового базиса записаны по столбцам, а именно Задача 8. Решение. Векторное равенство для этой ситуации: получается система Вычитая из 1-го уравнения 2-е, сразу видим Ответ. Координаты в новом базисе равны (1,1).
Задача 9. Решение. Векторное равенство: Видно из 2-го уравнения, что Ответ. Координаты в новом базисе (4,1). Задача 10. Дан базис в пространстве: Найти новые координаты вектора (0,3,4). Решение.
Система: Тогда из 2-го: Из 1-го уравнения: Ответ. Координаты в новом базисе
Практика № 8 Неопределённые системы ( Задача 1. Решить неоднородную систему Решение. Построим расширенную матрицу и преобразуем её.
Это равносильно такой системе уравнений Базисный минор в первых двух столбцах, 3-й столбец соответствует свободной переменной
Вот эти два выражения как раз и составляют общее решение системы. Задавая любое значение Общее решение можно записать также в виде такого вектора: Частные решения, например:
Ответ. Общее решение Задача 2. Решить неоднородную систему Решение. Запишем расширенную матрицу системы, впрочем, сразу при этом удобно будет поменять местами 1-ю и 3-ю строки, чтобы угловой элемент содержал именно число 1.
обнулим всё ниже углового элемента, для этого: из 2-й строки вычтем 1-ю, из 3-й удвоенную 1-ю, из 4-й 1-ю, домноженную на 4.
теперь можно поменять местами 2 и 3 строки, а также домножить на
затем из 4-й строки вычитаем 2-ю, чтобы продолжить стандартную процедуру метода Гаусса, потом видим что 3-я и 4-я стали одинаковы, тогда из 4-й вычитаем 3-ю. Получается, что 4-е уравнение 0 = 0.
Итак, осталось 3 уравнения, базисный минор легко заметить в первых трёх столбцах (там треугольная структура матрицы, и этот определитель явно отличен от 0). 4-й столбец не входит в базисный минор, то есть 4-я переменная свободная, т.е. когда будем записывать систему, переносим её через знак равенства во всех уравнениях.
Из последнего уравнения
Можно записать в виде вектора: Если задать, например, Ответ. Общее решение:
Задача 3. Решить неоднородную систему Решение. Запишем расширенную матрицу, вычтем из 2-й строки 1-ю. Здесь всего две строки, так что метод Гаусса проводится достаточно коротко.
Видим, что базисный минор можно выбрать в первых двух столбцах. Получается, что 3-я переменная свободная. Перепишем снова в виде системы, а не матрицы.
Выражаем
общее решение симстемы: Также записывается в виде вектора: Задавая какое-либо значение Ответ. Общее решение
Однородные системы. Задача 4. Решить однородную систему:
Решение. Видим, что отличие от предыдущей задачи в том, что справа нулевые константы. Если преобразовывать расширенную матрицу, то получим:
Видим, что справа всё равно как был, так и остаётся столбец из нулей, так что в будущем для однородных систем можно использовать только основную матрицу, ведь расширенная не несёт никакой новой информации, всё равно там справа нулевой столбец, и он не меняется при преобразованиях строк. Итак, получили систему Из 2-го:
Общее решение системы: Также записывается в виде вектора: Отличие от прошлой задачи в том, что на всех местах, где там были константы, здесь 0. Все переменные преобразовывались точно так же. Частные решения здесь отличаются тем, что задавая
То есть все тройки чисел будут пропорциональны какой-то одной. Если для неоднородной системы представить эти тройки чисел как точки в пространстве, то там они образовывали прямую,не проходящую через начало координат, а для однородной системы - проходящую через начало координат. Поэтому разумно выбрать для этой прямой всего 1 вектор, который задаёт её. Это как раз и есть ФСР (фундаментальная система решений). ФСР Ответ. Общее решение Задача 5. Решить однородную систему Решение. Можно записать основную матрицу и там вычесть 1-ю строку из 2-й, впрочем, можно для небольшой системы сделать это и сразу в системе, вычесть 1-е уравнение из 2-го. Получится:
Ранг равен 2, а неизвестных 3, 3-я неизвестная свободная, переносим вправо. Тогда: Из 2-го уравнения Общее решение: Присвоим ФСР состоит всего из одного вектора: Если бы, например, присвоили Ответ. Общее решение: Задача 6. Решить однородную систему Решение. Запишем основную матрицу, преобразуем её. снова представим в виде системы: базисный минор порядка 2, можно обвести в левом углу, поэтому 3-я и 4-я переменная - свободные. Здесь их уже две, так как
здесь
Общее решение: В виде вектора: Если поочерёдно присвоить значение 1 каждой из свободных переменных (а другая в это время 0) то получим гарантированно 2 линейно-независимых вектора, они не пропорциональны, так как число 1 в них на разных местах.
Эти 2 вектора { Ответ. Общее решение: ФСР это множество из 2 векторов: { Задача 7. Решить однородную систему, найти ФСР. Решение. Запишем основную матрицу системы и преобразуем её методом Гаусса.
Ранг матрицы равен 2, базисные столбцы 1-й и 2-й. Несмотря на то, что сначала могло показаться, что здесь будет одна свободная переменная (4 переменных и 3 уравнения), на самом деле здесь будет две свободных переменных, ведь 3-е уравнение оказалось линейной комбинацией первых двух. Снова возвращаемся от матрицы к системе уравнений. перенесём свободные неизвестные вправо:
будет Общее решение: В виде вектора: Построим ФСР из 2 векторов.
Так как здесь есть дроби, то для того, чтобы векторы в ФСР содержали только целые координаты, можно задавать не только 1, но и другое число, главное только чтобы в 3 и 4 координатах помещался невырожденный минор. Если мы задаём поочерёдно каждой свободной переменной какое-то число (не обязательно 1) а остальным 0, то линейная независимость этой системы векторов всё равно заведомо обеспечена. Ответ. Общее решение: ФСР из 2 векторов: Задача 8. Решить однородную систему, найти ФСР.
Решение. Преобразуем методом Гаусса основную матрицу системы.
Треугольная структура продолжилась до самой последней строки, и не проявилась строка из нулей, то есть ранг равен 3. Здесь всего одна свободная переменная. Развернём обратно эту матрицу, т.е. запишем в виде системы, а затем перенесём свободные переменные вправо.
Из последнего, Затем это всё в 1-е уравнение, получим ФСР: один вектор Ответ. Общее решение:
Задача 9. Решить однородную систему, найти ФСР.
Решение. Преобразуем методом Гаусса основную матрицу системы.
| ||
|
| Поделиться: |

 ,
,  .
.  , угол между ними 45 град.
, угол между ними 45 град. . Задача 2. Найти | [a,b] |.
. Задача 2. Найти | [a,b] |.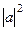
 =
=  .
. то объединим их, и получим
то объединим их, и получим 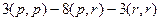 .
. и получаем
и получаем  . Ответ. 29.
. Ответ. 29. =
=  =
= 
 , но
, но  . Кроме того, чтобы объединить
. Кроме того, чтобы объединить  в одно слагаемое, здесь надо сначала у одной из них сменить знак.
в одно слагаемое, здесь надо сначала у одной из них сменить знак. =
= =
=  . Модуль векторного произведения
. Модуль векторного произведения  и
и  это площадь параллелограмма, где эти векторы являются сторонами, поэтому далее можно продолжить так:
это площадь параллелограмма, где эти векторы являются сторонами, поэтому далее можно продолжить так: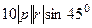 =
=  = 50. Ответ. 50.
= 50. Ответ. 50.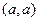 =
=  =
=  =
= =
= 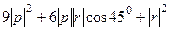 =
= =
=  = 257. Ответ. 257.
= 257. Ответ. 257. , если
, если  ,
,  , угол между p,q равен
, угол между p,q равен  .
. =
=  =
= =
=  =
=  = 92. Ответ 92.
= 92. Ответ 92. .
. .
.
 гипотенуза треугольника, поэтому
гипотенуза треугольника, поэтому  . Получается, что
. Получается, что  , то есть
, то есть 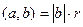 , откуда и следует
, откуда и следует  .
. на ось
на ось  .
. =
=  . Ответ. 2.
. Ответ. 2. .
. =
=  =
=  . Ответ.
. Ответ.  ,
,  .
.  , угол между ними 600.
, угол между ними 600. =
=  =
=  =
= =
=  =
= = 1227.
= 1227. =
= =
=  =
= =
=  =
= 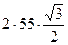 =
=  .
.
 .
.
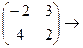



 .
. =
=  =
= 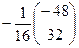 =
=  .
. .
. =
= 
 =
=  .
.
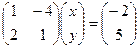 .
.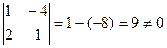 .
.



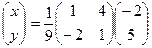 =
=  =
=  =
=  .
. =
= 
 =
=  .
. .
.


 из всех уравнений кроме первого, надо:
из всех уравнений кроме первого, надо:

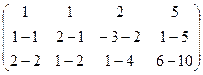 =
= 
 , нужно к 3-й строке просто прибавить 2-ю, так как знаки там противоположны. При этом структуру из нулей, которые уже получились слева, мы на последующем шаге всё равно никак не испортим, ведь там к 0 будет прибавляться 0 либо вычитаться 0, то есть ступенчатая структура там уже всё равно будет сохраняться.
, нужно к 3-й строке просто прибавить 2-ю, так как знаки там противоположны. При этом структуру из нулей, которые уже получились слева, мы на последующем шаге всё равно никак не испортим, ведь там к 0 будет прибавляться 0 либо вычитаться 0, то есть ступенчатая структура там уже всё равно будет сохраняться. =
= 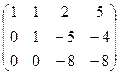

 В первом уравнении 3 неизвестных, а в каждом следующем всё меньше и меньше, а в последнем вообще только одна неизвестная. Именно этой цели мы и хотели добиться, приводя к треугольному виду: из последнего уравнения можно теперь сразу выразить
В первом уравнении 3 неизвестных, а в каждом следующем всё меньше и меньше, а в последнем вообще только одна неизвестная. Именно этой цели мы и хотели добиться, приводя к треугольному виду: из последнего уравнения можно теперь сразу выразить  . Затем с этой информацией мы поднимаемся в предпоследнее уравнение, где две неизвестных, впрочем, одна из них уже известна.
. Затем с этой информацией мы поднимаемся в предпоследнее уравнение, где две неизвестных, впрочем, одна из них уже известна.
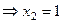 .
. . Итак,
. Итак, 
 .
. =2,
=2,  =1,
=1,  =1.
=1.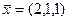 .
.
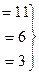
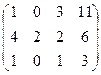

 =
= треугольная структура уже получилась.
треугольная структура уже получилась.
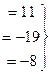 из 3-го уравнения
из 3-го уравнения  , подставляем во 2-е, там получается
, подставляем во 2-е, там получается 

 .
. ,
, 

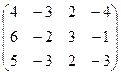

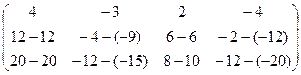 =
= 
 система:
система: 

 . Здесь тоже можно последовательно выразить все переменные, просто начинаем не с последней, а в другом порядке. К треугольному виду в этом случае можно до конца и не приводить.
. Здесь тоже можно последовательно выразить все переменные, просто начинаем не с последней, а в другом порядке. К треугольному виду в этом случае можно до конца и не приводить. , то есть
, то есть  .
. , т.е.
, т.е.  ,
,  .
. , откуда
, откуда  ,
,  .
. , в ведь то же время и
, в ведь то же время и  .
.
 а это очевидно, преобразуется к системе:
а это очевидно, преобразуется к системе:  . Ответ: координаты (2,1).
. Ответ: координаты (2,1). для этого примера, называется матрицей перехода от старого к новому базису, обозначается
для этого примера, называется матрицей перехода от старого к новому базису, обозначается  . Именно она и есть основная матрица системы, которую надо решить. Правая часть это старые координаты. Верно равенство
. Именно она и есть основная матрица системы, которую надо решить. Правая часть это старые координаты. Верно равенство  , т.е. новые координаты можно найти и так:
, т.е. новые координаты можно найти и так: 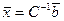 умножив обратную матрицу на старые координаты. Впрочем, это то же самое, что решить систему с квадратной матрицей матричным методом.
умножив обратную матрицу на старые координаты. Впрочем, это то же самое, что решить систему с квадратной матрицей матричным методом. Найти новые координаты вектора (3,2).
Найти новые координаты вектора (3,2). ,
, .
. Найти новые координаты вектора (5,4).
Найти новые координаты вектора (5,4).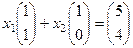 , система
, система  .
. , тогда
, тогда  .
.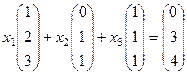 система:
система: 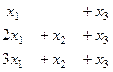


 =
= 
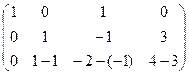 =
=  .
.
 . Из 3-го уравнения
. Из 3-го уравнения  , т.е.
, т.е.  , то есть
, то есть  .
. ).
).

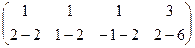 =
= 

 , её надо перенести вправо.
, её надо перенести вправо.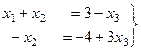 теперь надо выразить
теперь надо выразить  через
через  . Подставим теперь эту информацию в 1-е уравнение.
. Подставим теперь эту информацию в 1-е уравнение. , откуда
, откуда 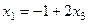 .
. .
.
 частное решение
частное решение  .
.
 .
.
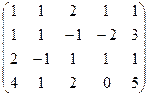
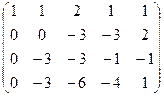
 три последних уравнения (там почти везде были знаки минус)
три последних уравнения (там почти везде были знаки минус)
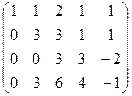



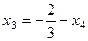 , подставляя это выражение во 2-е уравнение, выразим
, подставляя это выражение во 2-е уравнение, выразим  =
=  ,
,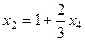 . Далее из 1-го уравнения:
. Далее из 1-го уравнения: =
=  ,
, . Итак, общее решение:
. Итак, общее решение: .
. получим частное решение:
получим частное решение: 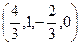 .
.
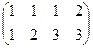

 переносим
переносим 
 ,через константы и
,через константы и  . Подставим это выражение в 1-е уравнение
. Подставим это выражение в 1-е уравнение , тогда
, тогда 
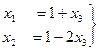
 .
.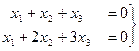


 базисный минор можно заметить в первых двух столбцах, так что
базисный минор можно заметить в первых двух столбцах, так что  . Теперь последовательно выражаем через свободную переменную две базисные переменные.
. Теперь последовательно выражаем через свободную переменную две базисные переменные. , а подставляя в 1-е, получим
, а подставляя в 1-е, получим , т.е.
, т.е.  .
.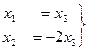 .
.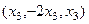 .
. ,
,  ,
,  ,
,  и так далее.
и так далее. .
.

 , тогда
, тогда  , а значит
, а значит  .
. .
. , получим остальные неизвестные.
, получим остальные неизвестные. . Все остальные решения пропорциональны этому.
. Все остальные решения пропорциональны этому. , получили бы
, получили бы  . Это потому, что всего одна свободная переменная.
. Это потому, что всего одна свободная переменная.



 , поэтому
, поэтому  . Перенесём их через знак равенства.
. Перенесём их через знак равенства.
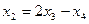 , подставим это в первое уравнение, чтобы выразить и
, подставим это в первое уравнение, чтобы выразить и  .
.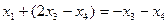 ,
, 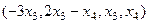 .
.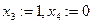 , получим
, получим 
 , получим
, получим  .
. частных решений, из которых можно составить любые другие частные решения. Любые их линейные комбинации будут частными решениями однородной системы.
частных решений, из которых можно составить любые другие частные решения. Любые их линейные комбинации будут частными решениями однородной системы.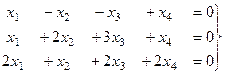



 .
.
 из 2 уравнения
из 2 уравнения  , подставим это в 1-е,
, подставим это в 1-е, , то есть
, то есть  .
.
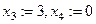 , получим
, получим 
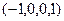 .
. .
.


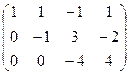
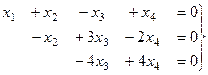

 , это подставим во 2-е и получим
, это подставим во 2-е и получим  .
. .
. .
. . ФСР:
. ФСР: 




