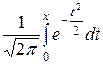Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка статистических гипотез.Содержание книги Поиск на нашем сайте
Пусть два предприятия производят однотипную продукцию и требуется сравнить параметры этой продукции (например, дальность полета снарядов, прочность кирпича на разлом, повышенное напряжение, при котором перегорает электрическая лампочка, и т.п.). Пусть Х и Y – значения исследуемого признака для единиц продукции первого и второго предприятия; это независимые случайные величины, распределенные по нормальному закону. Допустим, требуется сравнить МХ и MY. Производим выборки одинакового объема п и определяем по ним Мы выдвигаем гипотезу, что это расхождение случайно, то есть МХ = MY. Эта гипотеза называется основной, или нулевой. Конкурирующая гипотеза заключается в том, что отвергается основная. В данном случае она может быть сформулирована в виде МХ < MY. Задается уровень значимости α, означающий вероятность ошибки при оценке результата. Ошибка может быть двух видов: отвергается верная гипотеза (ошибка первого рода), или принимается неверная гипотеза (ошибка второго рода). Для оценки гипотезы разрабатывается специальным образом некоторая контрольная величина Т, приспособленная к данному типу задач. Определяется критическое значение величины Т, зависящее обычно от уровня значимости α и объема выборки п. Рассчитывается значение Т для данной выборки. Если оно оказывается меньше критического, то гипотеза принимается, если больше – отвергается. Таким образом, чтобы снизить вероятность ошибки первого рода, надо увеличивать критическое значение, а чтобы снизить вероятность ошибки второго рода, критическое значение следует уменьшать. Поэтому если выборочное значение Т оказывается больше критического, то мы гипотезу отвергаем с вероятностью ошибки α. Если же выборочное значение Т окажется меньше критического, то мы можем утверждать только, что предложенная гипотеза не противоречит результатам наблюдений. В рассматриваемом примере с дальностью полета снарядов будем считать дополнительно, что по результатам многолетних наблюдений известны средние квадратичные отклонения для этой величины: σ Х = 0,4; σ Y = 0,5. Тогда в качестве критерия можно использовать значение
Критическое значение находим по таблице функции Ф(х). Если задать уровень значимости 0,05, то критическое значение t 0 находим из условия Ф(t 0) = Получаем t 0 = 1,96. Так как t > t 0, то различие в результатах испытаний признается значительным, и гипотеза о равенстве средней дальности полета снарядов отвергается с вероятностью ошибки 0,05. Для различного типа задач вырабатываются различные критерии. Кроме задачи о равенстве средних значений, рассматриваются задачи о равенстве средних квадратичных отклонений, о проверке того, что две выборки относятся к одной и той же генеральной совокупности, и т.д. При этом может учитываться наличие дополнительной информации о генеральной совокупности. Рассмотрим задачу о законе распределения признака Х в генеральной совокупности. Выдвигается основная гипотеза о виде закона распределения, например, что закон является нормальным. Тогда конкурирующая гипотеза заключается в том, что закон имеет другой вид. По выборке рассчитываются параметры закона (для нормального закона это а и σ). По этим параметрам рассчитывается распределение значений признака Х для данного объема выборки, то есть частоты, с которыми эти значения должны появляться при данном объеме выборки (выравнивающие частоты). Эти частоты сравниваются с эмпирическими (полученными в результате эксперимента) и определяются расхождения между ними. По этим расхождениям специальным образом определяется значение χ2. По таблице χ2-распределения определяем критическое значение χ20. Эта таблица зависит от уровня значимости α и числа степеней свободы k = n – 3. Если χ2 > χ20, то гипотеза отвергается на уровне значимости α. Если χ2 < χ20, то утверждается, что гипотеза не противоречит результатам наблюдений. Для гипотезы о нормальном законе вычисления производятся следующим образом. Делается выборка объема n. В результате эксперимента получаем вариационный ряд вида
Считаем, что n = n 1 + n 2 +…+ nm и значения вариант идут с постоянным шагом h. Далее выполняем следующие шаги:
1) находим 2) вычисляем выравнивающие частоты по формулам
3) вычисляем величину 4) по таблице χ2 -распределения находим значение χ20 для данного уровня значимости α и числа степеней свободы k = n – 3; 5) если χ2 > χ20, то гипотеза отвергается на уровне значимости α. Если χ2 < χ20, то гипотеза не противоречит результатам наблюдений. Вычисления можно оформлять с помощью следующей таблицы.
Ввиду большого числа столбцов эту таблицу можно разбить на две. В первой вычисления производятся вплоть до столбца Пример 3. Проверить гипотезу о нормальном распределении для генеральной совокупности на уровне значимости α = 0,05 по следующему вариационному ряду, полученному экспериментальным путем.
Решение. Строим расчетную таблицу
Заполнив первые пять столбцов как при решении примера 2.1, последовательно находим: п = 80;
σ в = s = Следующие столбцы заполняются с помощью формул (1) и таблицы значений функции j(х). Для заполнения последнего столбца вычисляем множитель Далее строим вторую таблицу
Получили χ2 = 2,09. По таблице χ2 - распределения для k = m – 3 = 6 – 3 = 3 и α = 0,05 находим критическое значение χ20 = 7,82. Так как χ2 < χ20, то гипотеза о нормальном распределении не противоречит результатам эксперимента. Замечание. Для облегчения вычислений в первой таблице можно было использовать ложный нуль. Упражнения 4.1. Проверить гипотезу о нормальном распределении для генеральной совокупности на уровне значимости α = 0,05 по следующему вариационному ряду.
4.2. Проверить гипотезу о нормальном распределении для экзаменационных оценок на уровне значимости α = 0,05 по данным экзаменационных оценок по какому-нибудь предмету среди студентов вашей группы. Корреляционная зависимость В предыдущих главах часто встречались независимые случайные величины. Но на практике, конечно, встречаются разные степени зависимости. Крайний случай – функциональная зависимость, когда значения случайной величины Y однозначно определяются значениями случайной величины Х. Например, пусть в корзине лежат шарики разного размера, и случайным образом вытаскивается один шарик. Если Х – радиус шарика, а Y – его объем, то Y однозначно определяются через Х. Если же ввести третью случайную величину – массу шарика, то она может мало зависеть от Х, если шарики сделаны из разного материала. Если рассмотреть связь между ростом и массой человека, то понятно, что в среднем с увеличением роста увеличивается масса. Но эта зависимость только средняя, для отдельных людей могут быть значительные отклонения в ту или другую сторону. Такая зависимостьназывается корреляционной.
В нашем примере эта зависимость проявляется следующим образом. Пусть Х – рост, Y – вес человека. Зададим произвольное значение х, например, х = 175 см, и определим средний вес людей с ростом 175 см. Это можно сделать для каждого значения х, получим соответствующие значения y. В результате возникает функция y = g (x), которая называется регрессиейY на Х. В нашем примере эта функция означает средний вес людей с ростом х. Аналогично определяется функция x = f (y), задающая обратную зависимость – регрессия Х на Y. Графики этих функций называются линиями регрессии Y на Х и Х на Y соответственно. Особенно важным является случай, когда линии регрессии являются прямыми линиями. Для независимых случайных величин значения g (x) и f (y) являются постоянными, линии регрессии параллельны координатным осям, значит, перпендикулярны друг другу. Чем теснее зависимость, тем меньше острый угол между этими линиями. Они пересекаются в точке с координатами (MX, MY). При функциональной зависимости линии регрессии совпадают. Если случайные величины Х и Y независимы, то по свойствам математического ожидания M (XY) = MX . MY. Если же между Х и Y имеется зависимость, то это равенство нарушается, и за меру зависимости можно принять величину M (XY) – MX . MY. Но насколько велика степень зависимости можно понять, только если знать значения самих случайных величин Х и Y. Поэтому для характеристики степени зависимости принимают безразмерную величину, называемую коэффициентом корреляции: r = Можно показать, что Характер зависимости можно проследить на графике. По результатам наблюдений получаем пары соответствующих значений Х и Y. Эти пары отмечаем точками на координатной плоскости. Если между Х и Y есть линейная корреляционная зависимость, то точки более или менее плотно заполняют наклонную полосу, и чем теснее зависимость, тем уже полоса. Линии регрессии проходят через эту полосу примерно посередине. Если же зависимость отсутствует, то точки будут образовывать более или менее широкое пятно, которое может быть вытянуто по горизонтали или вертикали. Линии регрессии будут пересекать его вертикально и горизонтально.
Для нахождения коэффициента корреляции и расчета уравнений прямых регрессии по данным выборки пользуются следующей таблицей.
Столбцы xi и yi – это исходные данные. Найдя их сумму, вычисляем
При этом можно использовать ложный нуль, введя вспомогательные столбцы, как описано в разделе 2.2. Заполняем, используя найденные значения, остальные столбцы. Далее вычисляем
Найдя отсюда sx и sy, вычисляем коэффициент корреляции:
Выборочные уравнения прямых регрессии имеют вид
Пример 1. Оценить степень и характер зависимости между случайными величинами Х и Y по данным выборки, приведенным в таблице. Получить уравнения прямых регрессии. Построить график.
Решение. Строим расчетную таблицу
Так как r близок к 1, то связь между Х и Y достаточно тесная и прямая. Найдем уравнения прямых регрессии
y – 56,4 = 2,6 x – 51,4; y = 2,6 x + 5 – уравнение прямой регрессии Y на X;
x – 19,6 = 0,21 y – 11,6; 0,21 y = x – 8; y = 4,8 x – 38,1 – уравнение прямой регрессии X на Y. Строим график. Для проведения прямых регрессии найдем на них по две точки. Для этого зададим значения х и определяем соответствующие значения у по найденным формулам. Прямая регрессии Y на X: x = 17 Þ y = 2,6 . 17 + 5 = 49,2; x = 23 Þ y = 2,6 . 23 + 5 = 64,8. Прямая регрессии X на Y: x = 17 Þ y = 4,8 . 17 – 38,1 = 43,5; x = 22 Þ y = 4,8 . 22 – 38,1 = 67,5.
Прямая регрессии Y на X на графике менее крутая, чем прямая регрессии X на Y; это является общим правилом. Упражнения 5.1. Оцените степень и характер зависимости между случайными величинами Х и Y по данным выборки, приведенным в таблице. Получить уравнения прямых регрессии. Постройте график.
5.2. Оцените степень и характер зависимости между следующими случайными величинами, значения которых получите по выборке среди студентов вашей группы (можно отдельно среди юношей и девушек): а) ростом и массой; б) ростом и размером обуви; в) ростом и оценками на экзамене по какому-нибудь предмету; г) оценками на экзамене по двум предметам. Задания для контрольной работы Каждый студент подставляет в задания свои значения параметров а и b. 1. Выборочная совокупность задана таблицей:
Найдите выборочную среднюю, исправленную выборочную дисперсию, исправленное среднее квадратичное отклонение. Постройте полигон распределения.
2. Задано распределение выборки объема п = 100 для случайной величины. Найдите выборочное среднее, исправленную выборочную дисперсию, исправленное среднее квадратичное отклонение. Постройте гистограмму частот.
3. Найдите с надежностью g = 0,95 доверительный интервал для математического ожидания а нормально распределенной случайной величины из задачи 2. Индивидуальные задания для студентов Каждый студент подставляет в задания свои значения параметров а и b. 1. Проверьте гипотезу о нормальном распределении генеральной совокупности при уровне значимости g = 0,05 по выборке, заданной таблицей:
2. Найдите выборочные уравнения прямых регрессии Y на Х и Х на Y по данным таблицы. Постройте графики. Вычислите коэффициент корреляции. Сделайте вывод об уровне и направлении зависимости между Х и Y.
Справочный материал Таблица значений функции Гаусса j(х) =
Таблица значений функции Ф(х) =
F(3,80) = 0,499928; F(4,00) = 0,499968; F(4,50) = 0,499997; F(5,00) = 0,4999997. Таблица распределения Стьюдента t g = t (g, n)
Таблица c2-распределения с уровнем значимости p и числом степеней свободы k = m – 3
Предметный указатель биномиальное распределение, 26 благоприятствующее событие, 5 варианта, 31 вариационный ряд, 31 вероятность, 3 вероятность произведения двух событий, 13 вероятность произведения независимых событий, 12 вероятность произведения нескольких событий, 13 выборка, 30 выборочная дисперсия, 33 выборочная средняя, 33 выборочное среднее, 31 выравнивающие частоты, 39 генеральная совокупность, 30 гистограмма, 31 дисперсия, 21 доверительный интервал, 36 достоверное событие, 5 закон больших чисел, 27 закон распределения случайной величины, 19 интегральная теорема Муавра – Лапласа, 18 исправленная выборочная дисперсия, 34 испытание, 3 классическое определение вероятности, 9 корреляционная зависимость, 42 коэффициент корреляции, 42 ложный нуль, 35 локальная теорема Муавра – Лапласа, 17 математическое ожидание, 21 математическое ожидание дискретной случайной величины, 21 математическое ожидание непрерывной случайной величины, 24 медиана, 32 мода, 32 невозможное событие, 4 независимые случайные величины, 20 несмещенность, 33 несовместные события, 5 нормальное распределение, 26 относительная частота, 31 относительная частота появления события, 3 перестановка, 6 плотность вероятности случайной величины, 24 полигон частот, 31 принцип произведения, 6 принцип суммы, 6 Произведение событий, 4 пространство элементарныхсобытий, 3 противоположное событие, 4 равновозможное распределение, 26 равномерное распределение, 26 размах, 32 размещение, 7 разность событий, 4 регрессия, 42 репрезентативность, 31 ряд распределения случайной величины, 20 случайная величина, 19 случайная величина дискретная, 19 случайная величина непрерывная, 19 состоятельность, 33 сочетание, 7 среднее квадратичное отклонение, 22 статистическое определение вероятности, 3 сумма событий, 4 схема Бернулли, 16 теорема Бернулли, 28 теорема Чебышёва, 28 условная вероятность, 13 факториал, 6 формула Байеса, 15 формула Бернулли, 16 формула полной вероятности, 14 функция распределения случайной величины, 23 центральная предельная теорема, 27 эффективность оценки, 34 Литература 1. Гусева, Е. Н. Теория вероятностей и математическая статистика. Учебное пособие./ Е.Н. Гусева. 5-е изд., стереотип. – М.: Флинта, 2011. – 220 с. 2. Гмурман, В.Е.. Теория вероятностей и математическая статистика: Учебное пособие для студ. вузов/ В.Е. Гмурман. – 12-е изд., перер. – М: Высшее образование, 2007. – 479 с. 3. Баврин, И.И. Теория вероятностей и математическая статистика: Учебник для студ.высших педагогич. учебных заведений/ И.И. Баврин. – М: Высш. шк., 2005. – 160 с. 4. Баврин, И.И. Краткий курс теории вероятностей и математическая статистика. / И.И. Баврин, В.Л. Матросов. – М.: Прометей, 1989. – 136 с. 5. Свешников, А.А. Сборник задач по теории вероятностей, математической статистике и теории случайных величин/ А.А. Свешников – М.: Лань, 2008. – 448 с. Содержание 1. Теория вероятностей. 3 1.1 Понятие вероятности. 3 1.2 Пространство элементарных событий. 3 1.3 Элементы комбинаторики. 3 1.4 Классическое определение вероятности. 3 1.5 Теоремы сложения. Произведение независимых событий. 3 1.6 Условная вероятность. 3 1.7 Формула полной вероятности. 3 1.8 Повторные независимые испытания. 3 1.9 Случайные величины.. 3 1.10 Непрерывные случайные величины.. 3 1.11 Основные законы распределения случайных величин. 3 1.12 Закон больших чисел. 3 2. Математическая статистика. 3 2.1 Выборочный метод. 3 2.2 Точечная оценка параметров. 3 2.3 Доверительные интервалы.. 3 2.4 Проверка статистических гипотез. 3 2.5 Корреляционная зависимость. 3 Справочный материал. 3 Предметный указатель. 3 Литература. 3
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 242; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.76.111 (0.011 с.) |

 и
и  . Например, средняя дальность полета снарядов при п = 100 испытаниях оказалась
. Например, средняя дальность полета снарядов при п = 100 испытаниях оказалась  =
=  =
=  = 3,12.
= 3,12.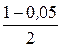 = 0,475.
= 0,475.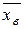 и σ в = s, как описано в разделе 2.2;
и σ в = s, как описано в разделе 2.2;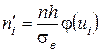 , где
, где  ; (1)
; (1) ;
;


 = 15,7;
= 15,7; = 7,77;
= 7,77; = 2,79.
= 2,79.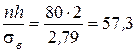 .
. .
. . При этом если r = ±1, то между Х и Y имеет место функциональная линейная зависимость: прямая при r = 1, обратная при r = –1 (то есть при увеличении Х уменьшается Y). Если Х и Y независимы, то r = 0. Но обратное неверно. Между Х и Y может быть даже функциональная зависимость, но если она на одном участке прямая, а на другом обратная, то эти участки могут компенсировать друг друга и сделать коэффициент корреляции равным или близким к 0. Поэтому если ï r ï близок к 1, то мы делаем вывод, что зависимость тесная. Если же ï r ï близок к 0, то вывод о слабой зависимости еще требует своего подтверждения.
. При этом если r = ±1, то между Х и Y имеет место функциональная линейная зависимость: прямая при r = 1, обратная при r = –1 (то есть при увеличении Х уменьшается Y). Если Х и Y независимы, то r = 0. Но обратное неверно. Между Х и Y может быть даже функциональная зависимость, но если она на одном участке прямая, а на другом обратная, то эти участки могут компенсировать друг друга и сделать коэффициент корреляции равным или близким к 0. Поэтому если ï r ï близок к 1, то мы делаем вывод, что зависимость тесная. Если же ï r ï близок к 0, то вывод о слабой зависимости еще требует своего подтверждения.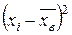



 ;
;  .
. ;
;  ;
;  .
.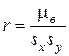 .
. – регрессия y на х;
– регрессия y на х; – регрессия х на y.
– регрессия х на y. = 19,6;
= 19,6;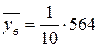 = 56,4;
= 56,4; = 3,58;
= 3,58;  = 1,89;
= 1,89; = 45,8;
= 45,8;  = 6,77;
= 6,77; =9,4;
=9,4; = 0,73.
= 0,73. ;
; ;
;
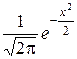 .
.