
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 5. Статистическое изучение корреляционных взаимосвязейСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Виды связей между показателями При изучении социально-экономических явлений часто приходится иметь дело с взаимосвязанными показателями. Связь между показателями может быть функциональной и статистической. Связь между величинами x и y называется функциональной, если каждому значению величины x соответствует одно и только одно значение величины y. Это означает, что при изменении значения x значение y изменяется строго определенным образом. Связь между величинами x и y называется статистической, если при многократном повторении наблюдения одному и тому же значению x могут соответствовать разные значения y. Например, с одинаковых участков земли при равных количествах удобрений снимают разный урожай. Это объясняется влиянием таких случайных факторов, как количество осадков, температура воздуха и др. Статистическая связь обнаруживается только при массовом наблюдении как статистическая закономерность. В частном случае статистическая зависимость проявляется в том, что при изменении одно величины изменяется среднее значение другой. Такой тип статистической зависимости называется корреляционной зависимостью. Если среднее значение результативного признака y зависит от одного факторного признака x, корреляция называется парной, а если от нескольких факторных признаков – множественной. Изучение корреляционных связей сводится к решению следующих задач. 1. Выявление наличия или отсутствия корреляционной связи между изучаемыми признаками. 2. Измерение тесноты связи между признаками. Это исследование называется корреляционным анализом. 3. Определение уравнения регрессии, то есть функциональной зависимости среднего значения результативного признака от факторных признаков. Такое исследование называется регрессионным анализом. Рассмотрим методы выявления корреляционной зависимости.
Метод группировки Чтобы выявить наличие корреляционной зависимости между двумя признаками, проводится группировка единиц совокупности по факторному признаку x и для каждой группы вычисляется среднее значение результативного признака
Пример. Распределение издержек обращения по группам предприятий оптовой торговли приведено в таблице. Таблица 7
В последнем столбце приведены средние издержки обращения по каждой группе предприятий. Из таблицы видно, что чем крупнее предприятие, тем меньше издержки обращения. Таким образом, существует корреляционная связь между объемом товарооборота и средними издержками обращения. Результаты группировки оформляются в виде корреляционной таблицы. В корреляционной таблице в строках указываются значения факторного признака x, а на пересечении указывается число совпадений значений x и y. Пример. Таблица 8
Из таблицы видно, что с увеличением x групповые средние увеличиваются. Такая связь называется прямой. Если с увеличением x групповые средние уменьшаются, связь называется обратной. Таким образом, между x и y существует прямая корреляционная связь. Если частоты расположены в клетках таблицы беспорядочно, это говорит об отсутствии связи. Если частоты сконцентрированы около диагонали из верхнего левого угла в нижний правый, это говорит о прямой корреляционной зависимости между x и y, если около второй диагонали – об обратной корреляционной зависимости.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 651; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.166.5 (0.008 с.) |

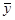 . Если корреляционная связь существует, то в изменении среднего значения
. Если корреляционная связь существует, то в изменении среднего значения 


