
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства выборочного коэффициента корреляции Спирмена.Содержание книги
Поиск на нашем сайте
Если между А и В имеется «полная прямая зависимость», то есть ранги совпадают при всех i, то ρВ = 1. Действительно, при этом di = 0, и из формулы (12.4) следует справедливость свойства 1. Если между А и В имеется «противоположная зависимость», то ρВ = - 1. В этом случае, преобразуя di = (2i – 1) – n, найдем, что В остальных случаях -1 < ρB < 1, причем зависимость между А и В тем меньше, чем ближе | ρB | к нулю.
Итак, требуется при заданном уровне значимости α проверить нулевую гипотезу о равенстве нулю генерального коэффициента ранговой корреляции Спирмена ρг при конкурирующей гипотезе Н1: ρг ≠ 0. Для этого найдем критическую точку:
где п – объем выборки, ρВ – выборочный коэффициент ранговой корреляции Спирмена, tкр (α, k) – критическая точка двусторонней критической области, найденная по таблице критических точек распределения Стьюдента, число степеней свободы k = n – 2. Тогда, если | ρB | < Tкр, то нулевая гипотеза принимается, то есть ранговая корреляционная связь между признаками незначима. Если | ρB | > Tкр, то нулевая гипотеза отвергается, и между признаками существует значимая ранговая корреляционная связь. Можно использовать и другой коэффициент – коэффициент ранговой корреляции Кендалла. Рассмотрим ряд рангов у1, у2,…, уп, введенный так же, как и ранее, и зададим величины Ri следующим образом: пусть правее у1 имеется R1 рангов, больших у1; правее у2 – R2 рангов, больших у2 и т.д. Тогда, если обозначить R =R1 + R2 +…+ Rn-1, то выборочный коэффициент ранговой корреляции Кендалла определяется формулой
где п – объем выборки. Замечание. Легко убедиться, что коэффициент Кендалла обладает теми же свойствами, что и коэффициент Спирмена. Для проверки нулевой гипотезы Н0: τг = 0 (генеральный коэффициент ранговой корреляции Кендалла равен нулю) при альтернативной гипотезе Н1: τг ≠ 0 необходимо найти критическую точку:
где п – объем выборки, а zкр – критическая точка двусторонней критической области, определяемая из условия Если | τB | < Tкр, то нулевая гипотеза принимается (ранговая корреляционная связь между признаками незначима). Если | τB | > Tкр, то нулевая гипотеза отвергается (между признаками существует значимая ранговая корреляционная связь).
Регрессионный анализ. Рассмотрим выборку двумерной случайной величины (Х, Y). Примем в качестве оценок условных математических ожиданий компонент их условные средние значения, а именно: условным средним M (Y / x) = f (x), M (X / y) = φ (y). Условные средние
- выборочное уравнение регрессии Y на Х,
- выборочное уравнение регрессии Х на Y. Соответственно функции f*(x) и φ*(у) называются выборочной регрессией Y на Х и Х на Y, а их графики – выборочными линиями регрессии. Выясним, как определять параметры выборочных уравнений регрессии, если сам вид этих уравнений известен. Пусть изучается двумерная случайная величина (Х, Y), и получена выборка из п пар чисел (х1, у1), (х2, у2),…, (хп, уп). Будем искать параметры прямой линии среднеквадратической регрессии Y на Х вида Y = ρyxx + b, (12.10) Подбирая параметры ρух и b так, чтобы точки на плоскости с координатами (х1, у1), (х2, у2), …, (хп, уп) лежали как можно ближе к прямой (12.10). Используем для этого метод наименьших квадратов и найдем минимум функции
Приравняем нулю соответствующие частные производные:
В результате получим систему двух линейных уравнений относительно ρ и b:
Ее решение позволяет найти искомые параметры в виде:
При этом предполагалось, что все значения Х и Y наблюдались по одному разу. Теперь рассмотрим случай, когда имеется достаточно большая выборка (не менее 50 значений), и данные сгруппированы в виде корреляционной таблицы
Здесь nij – число появлений в выборке пары чисел (xi, yj). Поскольку
Можно решить эту систему и найти параметры ρух и b, определяющие выборочное уравнение прямой линии регрессии:
Но чаще уравнение регрессии записывают в ином виде, вводя выборочный коэффициент корреляции. Выразим b из второго уравнения системы (12.14):
Подставим это выражение в уравнение регрессии:
где
и умножим равенство (22.8) на
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 316; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.189.164 (0.01 с.) |

 , тогда из (12.4)
, тогда из (12.4) 
 , (12.5)
, (12.5) (12.6)
(12.6) , (12.7)
, (12.7) по таблицам для функции Лапласа.
по таблицам для функции Лапласа. назовем среднее арифметическое наблюдавшихся значений Y, соответствующих Х = х. Аналогично условное среднее
назовем среднее арифметическое наблюдавшихся значений Y, соответствующих Х = х. Аналогично условное среднее 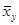 - среднее арифметическое наблюдавшихся значений Х, соответствующих Y = y. В лекции 11 были выведены уравнения регрессии Y на Х и Х на Y:
- среднее арифметическое наблюдавшихся значений Х, соответствующих Y = y. В лекции 11 были выведены уравнения регрессии Y на Х и Х на Y: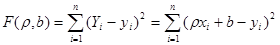 . (12.11)
. (12.11)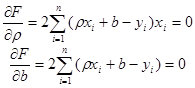 .
.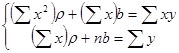 . (12.12)
. (12.12)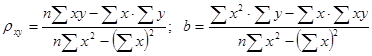 . (12.13)
. (12.13)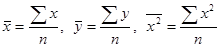 , заменим в системе (22.5)
, заменим в системе (22.5) 
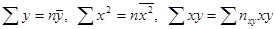 , где пху – число появлений пары чисел (х, у). Тогда система (22.5) примет вид:
, где пху – число появлений пары чисел (х, у). Тогда система (22.5) примет вид: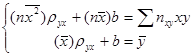 . (12.14)
. (12.14)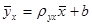 .
.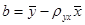 .
.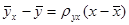 . Из (12.14)
. Из (12.14) , (12.15)
, (12.15) Введем понятие выборочного коэффициента корреляции
Введем понятие выборочного коэффициента корреляции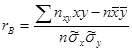
 :
: 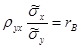 , откуда
, откуда 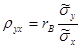 . Используя это соотношение, получим выборочное уравнение прямой линии регрессии Y на Х вида
. Используя это соотношение, получим выборочное уравнение прямой линии регрессии Y на Х вида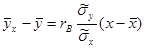 . (12.16)
. (12.16)


