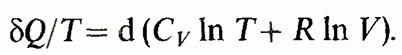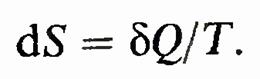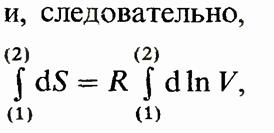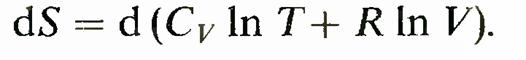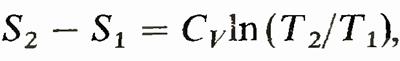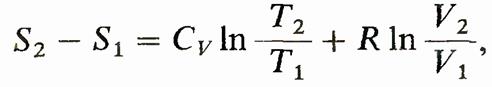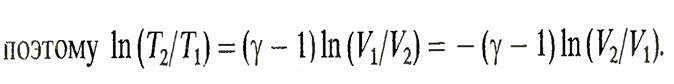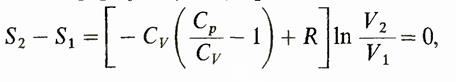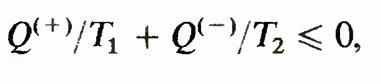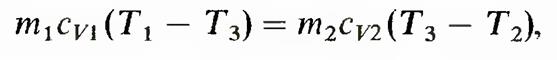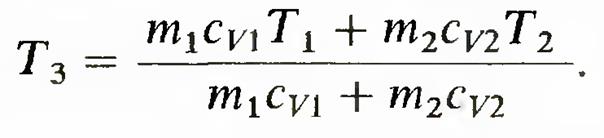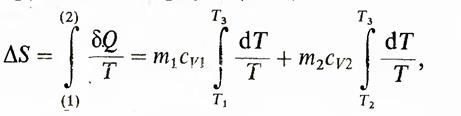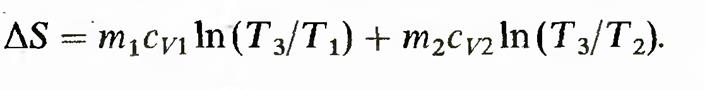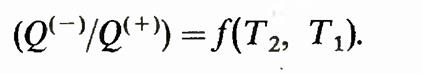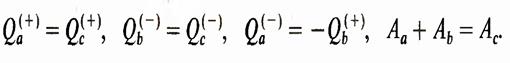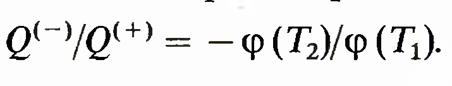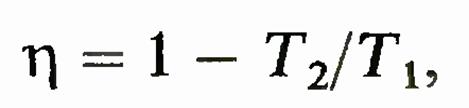Энтропия,Энтропия идеального.Вторая теорема Карно.Неравенство Клаузиуса.Изменени энтропии при необратимых процессах.

Разделив обе части равенства, выражающего первое начало термодинамики, на Т, получим

Подставляя р/Т= R/V и учитывая, что dT/T= dlnT dV/V= dln V, получаем1

Правая часть равенства представляет собой полный дифференциал. Следовательно,

левая часть bQ/T также полный дифференциал. Функция состояния, дифференциалом которой является bQ/T, называется энтропией и обозначается S. Таким образом,

Применим формулу для вычисления изменения энтропии в изотермическом процессе (Т— const), где энергетическое состояние газа остается неизменным, а всевозможные изменения характеристик обусловлены лишь изменением объема. Для этого случая

что после интегрирования дает

После несколькіх преобразованій получаем:

 

энтропия S определяется логарифмом числа микросостояний, посредством которых реализуется рассматриваемое макросостояние,т.е.

Это равенство называется формулой Больцмана.

Расчет изменения энтропии в процессах идеального газа проводится по формуле 1

При изохорическом процессе (d.V = 0)

при увеличении объема энтропия возрастает, при уменьшении — уменьшается.

т. е. при увеличении температуры энтропия увеличивается. Этот результат объясняется

следующим: средняя энергия частиц растет с ростом температуры, а поэтому увеличивается и число возможных энергетических состояний.

При адиабатическом процессе получаем

Тогда формула принимает вид

Таким образом, при адиабатическом обратимом процессе энтропия не изменяется. Нетрудно

понять, почему это происходит. При адиабатическом расширении газа за счет увеличения объема энтропия увеличивается, однако за счет уменьшения температуры, которое при этом происходит, она уменьшается и эти две тенденции полностью компенсируют друг друга.

Вторая теорема Карно. к. п. д. обратимого цикла Карно больше к. п. д. любого другого обратимого цикла, в котором максимальные и минимальные температуры равны соответственно температуре нагревателя и температуре холодильника цикла Карно.

Математически формулируется.

Знак минус в этом неравенстве учитывает, что знаки Q(+) и Q(-} различны.

Соотношение 2, переписанное в виде

называется неравенством Клаузиуса для цикла Карно. Очевидно, что знак равенства относится к обратимому циклу. Неравенство Клаузиуса

в неравенстве Клаузиуса знак равенства относится к обратимым процессам, а знак неравенства — к необратимым.

Изменение энтропии в необратимых процессах. Вычисление основывается на том,

что энтропия является функцией состояния. Если система перешла из одного состояния

в другое посредством необратимого процесса, то логично мысленно перевести систему из первого состояния во второе с помощью некоторого обратимого процесса и рассчитать происходящее при этом изменение энтропии. Оно равно

изменению энтропии при необратимом процессе.

Рассмотрим изменение энтропии при выравнивании температуры двух тел, приведенных в тепловой контакт. Обозначим массы, удельные теплоемкости при постоянном

объеме и температуры первого и второго тел соответственно m1,cv1, T1 и m2, cv2,

Т2. При тепловом контакте температуры тел выравниваются. Будем считать для упрощения расчета, что теплообмен происходит при постоянном объеме (Vi2 = const) каждого из тел, теплоемкости сv1 и cv2 не зависят от температуры, T1> Т2. Для определения температуры T3, которую будут иметь тела после достижения термодинамического равновесия, можно написать уравнение

из которого следует, что

изменение энтропии можно рассчитать с помощью обратимого процесса по формуле

где bQ — mcvdT. Вычислив интегралы, получим

Это и есть изменение энтропии в необратимом процессе

28.Термодинамическое равновесие.Термометры.Шкала Кельвина. Термодинамическая шкала температур. Доказано, что

к. п. д.

имеет одинаковое значение для всех обратимых машин,

работающих с нагревателем температуры Т1 и с холодильником температуры Т2. Поэтому Q(-)/Q{+) является функцией тлько от T1 и Т2:

Две обратимые машины а и b в комбинации составляют одну обратимую машину, к. п. д. которой должен быть равным к. п. д. машины с. Это означает, что

Соотношение для этих машин имеет вид

При преобразованиях получаем.

где ф — новая функция. Тем самым доказано, что отношение количеств теплоты в цикле Карно выражается в виде

В принципе функцию ф можно выбрать бесчисленными способами и тем самым

получить множество различных шкал температур. Кельвин предложил выбрать простейшую зависимость5

которая фиксирует термодинамическую шкалу температур. В ней коэффициент полезного действия обратимой машины, работающей по циклу Карно, равен

во всем предшествующем

изложении буква Т означала температуру в одной и той же шкале и являлась термодинамической температурой.

Отрицательная термодинамическая температура. Исходя из второго начала термодинамики, можно доказать невозможность отрицательных термодинамических температур.

Пусть тело с отрицательной температурой Т2 выбрано в качестве холодильника

в цикле Карно. Тогда правая часть равенства 5 положительна, как и Q{+) — количество теплоты, взятое у нагревателя. Следовательно, Q(-) также положительная величина. Это означает, что такая машина должна брать теплоту также из холодильника, т. е. берется теплота и из нагревателя и из холодильника и нацело превращается в работу. Но это противоречит второму началу термодинамики в формулировке Кельвина и, следовательно, неосуществимо. Поэтому отрицательная температура не возможна.