
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энергетические уровни в атоме водородаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Задавая
Рис. 4.1.4 В соответствии со вторым постулатом Бора, переходя из стационарного состояния с большей энергией в стационарное состояние с меньшей энергией, атом испускает квант Полагая в формуле для частоты спектральных линий Теория Бора позволяет объяснить и спектр поглощения атома водорода. Так как свободные атомы водорода обычно находятся в основном состоянии ( Подводя итог, можно заключить, что теория Бора с полной отчетливостью показала неприменимость классической физики к внутриатомным явлениям и главенствующее значение квантовых законов в микромире. Однако после первых успехов теории яснее проявились ее недочеты. Неудачной была попытка построения теории атома гелия – одного из простейших атомов после атома водорода. Самой слабой стороной теории Бора, вызвавшей последующие неудачи, была ее внутренняя противоречивость: она не была ни последовательно классической, ни последовательно квантовой теорией. В настоящее время ясно, что она могла быть только переходным этапом на пути создания последовательной теории атомных явлений. Пример 5. Определить частоту света, излучаемого водородоподобным ионом при переходе электрона на уровень с главным квантовым числом Решение. Частота излучаемого света по обобщенной формуле Бальмера равна: Пример 6. Во сколько раз увеличится радиус орбиты электрона у атома водорода, находящегося в основном состоянии, при возбуждении его фотоном энергией Решение. Энергия атома водорода
Отсюда получаем: Пример 7. Атом водорода освещается ультрафиолетовым излучением с длиной волны Решение. На атом водорода падают фотоны с энергией
Основы квантовой механики Гипотеза де Бройля
Невозможность объяснить с помощью теории Бора строение атомов различных элементов сделала необходимым критический пересмотр основ квантовой теории и представлений о природе элементарных частиц (электронов, протонов и т. п.). Возник вопрос о том, насколько полным является представление электрона в виде малой механической частицы, характеризуемой определенными координатами и импульсом (скоростью). В результате развития науки о природе света выяснилось, что в оптических явлениях обнаруживается своеобразный дуализм (двойственность). Наряду с такими свойствами света, которые самым непосредственным образом свидетельствуют о его волновой природе (явления интерференции, дифракции), имеются и другие свойства, столь же непосредственно обнаруживающие его корпускулярную природу (тепловое излучение, фотоэффект, эффект Комптона). В 1924 г. французский ученый Луи де Бройль выдвинул смелую гипотезу о том, что дуализм присущ не только оптическим явлениям, но и имеет универсальное значение. Допуская, что частицы вещества наряду с корпускулярными свойствами имеют и волновые, де Бройль связал с каждым микрообъектом, с одной стороны, корпускулярные характеристики: энергию Гипотеза де Бройля вскоре была блестяще подтверждена экспериментально. Сначала американские физики Девиссон и Джермер (1927 г.) обнаружили, что пучок электронов, рассеивающийся от кристаллической пластинки, дает дифракционную картину. Затем Томсон и Тартаковский независимо друг от друга получили дифракционную картину при прохождении электронного пучка через металлическую фольгу. В этом случае опыт осуществлялся следующим образом. Пучок электронов, ускоренный разностью потенциалов порядка нескольких десятков киловольт, проходил через тонкую металлическую фольгу и попадал на фотопластинку. Электрон при ударе о фотопластинку оказывал на нее такое же действие, как и фотон. Полученная дифракционная картина поразительно точно совпадала с дифракционной картиной, полученной при прохождении рентгеновских лучей через металлическую фольгу. Советский физик Фабрикант (1948 г.), пропуская очень разреженный пучок электронов через фольгу (промежуток времени между двумя электронами в 104 раз был больше времени прохождения электроном прибора), после длительной экспозиции получил дифракционную картину, не отличающуюся от дифракционных картин, получаемых для потоков электронов при короткой экспозиции. Этим было доказано, что волновые свойства частиц не являются свойством их совокупности, а присущи каждой частице в отдельности. Таким образом, любой частице, обладающей импульсом, можно сопоставить волновой процесс с длиной волны, определяемой по формуле де Бройля: Впоследствии были обнаружены дифракционные явления у нейтронных, атомных и молекулярных пучков, причем длины волн соответствовали соотношению де Бройля. Но если волновые свойства присущи микрочастицам, то они должны быть присущи и макроскопическим телам. Почему же они не обнаруживаются экспериментально? Потому что длина волны, соответствующая макроскопическому телу, очень мала и не может быть измерена. В самом деле, пусть тело массой 1 кг движется со скоростью 100 м/с. Его импульс
Значит Пример 1. Вычислить длину волны де Бройля для молекулы серебра, движущейся со скоростью, совпадающей со средней квадратичной скоростью молекул при температуре 27°С. Будет ли испытывать эта молекула дифракцию при прохождении щели в Решение. Средняя квадратичная скорость молекул Пример 2. Параллельный пучок электронов, прошедший ускоряющую разность потенциалов
Рис. 4.2.1
Решение. Ширина дифракционной картины
|
||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 1448; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

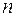 различные целочисленные значения, для атома водорода
различные целочисленные значения, для атома водорода 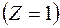 получим возможные уровни энергии. Схематически они представлены на рис. 4.1.4. Энергия атома водорода с увеличением
получим возможные уровни энергии. Схематически они представлены на рис. 4.1.4. Энергия атома водорода с увеличением  при
при 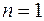 и
и 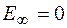 при
при 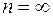 ). Если
). Если 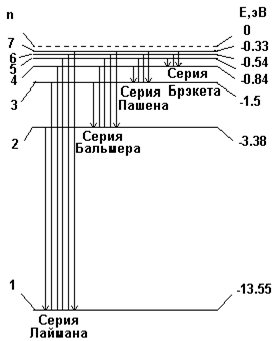
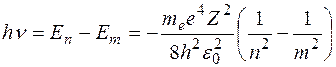 . Для частоты излучения имеем:
. Для частоты излучения имеем:  . Сопоставляя последнее выражение с обобщенной формулой Бальмера, получаем выражение для постоянной Ридберга:
. Сопоставляя последнее выражение с обобщенной формулой Бальмера, получаем выражение для постоянной Ридберга: 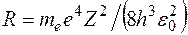 . Эта формула дает значение
. Эта формула дает значение  , хорошо совпадающее с опытом, что подтверждает верность постулатов Бора для водородоподобных систем.
, хорошо совпадающее с опытом, что подтверждает верность постулатов Бора для водородоподобных систем. и
и 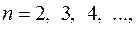 получаем группу линий, образующих серию Лаймана. Совершенно аналогично можно получить и линии остальных серий спектра атома водорода.
получаем группу линий, образующих серию Лаймана. Совершенно аналогично можно получить и линии остальных серий спектра атома водорода. раз.
раз. . Радиус n -й орбиты
. Радиус n -й орбиты 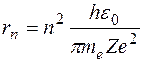 . Отсюда отношение радиусов n -й и m -й орбит равно:
. Отсюда отношение радиусов n -й и m -й орбит равно: 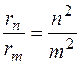 . По условию задачи это отношение равно
. По условию задачи это отношение равно 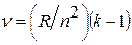 .
.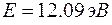 ?
?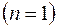 равна:
равна: 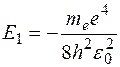 . При сообщении такому атому энергии
. При сообщении такому атому энергии 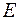 он перейдет в состояние с энергией:
он перейдет в состояние с энергией: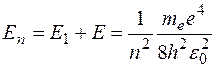 .
. . Производя вычисления, находим:
. Производя вычисления, находим:  .
.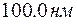 . Определить, какие спектральные линии появятся в спектре водорода.
. Определить, какие спектральные линии появятся в спектре водорода.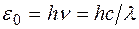 . Здесь
. Здесь 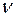 и
и  – частота и длина волны падающего фотона,
– частота и длина волны падающего фотона, 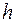 – постоянная Планка. Атом переходит в возбужденное состояние с энергией
– постоянная Планка. Атом переходит в возбужденное состояние с энергией 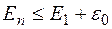 . Здесь
. Здесь 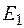 – энергия атома в основном состоянии. Знак «
– энергия атома в основном состоянии. Знак «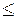 » взят с учетом того, что энергия может восприниматься атомом только определенными порциями. В нашем случае
» взят с учетом того, что энергия может восприниматься атомом только определенными порциями. В нашем случае 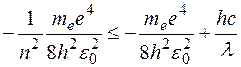 . Выражая отсюда
. Выражая отсюда 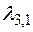 – при переходе с третьей орбиты на первую;
– при переходе с третьей орбиты на первую;  – при переходе с третьей орбиты на вторую;
– при переходе с третьей орбиты на вторую; 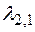 – при переходе со второй орбиты на первую. По обобщенной формуле Бальмера имеем:
– при переходе со второй орбиты на первую. По обобщенной формуле Бальмера имеем: 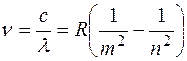 . Вычисляя длину волны для указанных переходов, получим:
. Вычисляя длину волны для указанных переходов, получим: 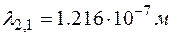 ;
; 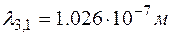 ;
; 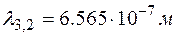 .
.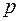 , а с другой – волновые характеристики: частоту
, а с другой – волновые характеристики: частоту 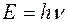 и
и 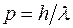 .
.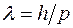 .
.
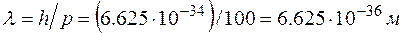 . Такую длину волны измерить невозможно, поэтому считается, что макротела проявляют только корпускулярные свойства.
. Такую длину волны измерить невозможно, поэтому считается, что макротела проявляют только корпускулярные свойства.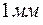 ?
?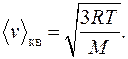 Здесь
Здесь 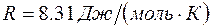 – универсальная газовая постоянная,
– универсальная газовая постоянная,  – температура,
– температура, 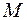 – молярная масса (для серебра
– молярная масса (для серебра  ). Длина волны де Бройля
). Длина волны де Бройля 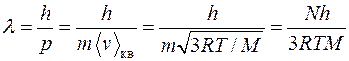 . Здесь
. Здесь 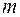 – масса молекулы,
– масса молекулы, 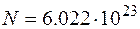 – число Авогадро. Подставляя числовые значения, получаем:
– число Авогадро. Подставляя числовые значения, получаем:  . Длина волны сравнима с шириной щели. Значит, дифракция будет иметь место.
. Длина волны сравнима с шириной щели. Значит, дифракция будет иметь место.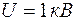 , падает на щель шириной
, падает на щель шириной 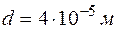 (рис. 4.2.1). Определить ширину
(рис. 4.2.1). Определить ширину 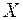 изображения щели на люминесцентном экране, находящимся на расстоянии
изображения щели на люминесцентном экране, находящимся на расстоянии 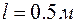 от щели. Интенсивностью дифракционных максимумов первого и более высоких порядков можно пренебречь.
от щели. Интенсивностью дифракционных максимумов первого и более высоких порядков можно пренебречь.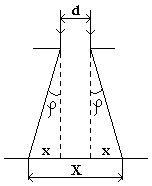
 . Условие минимума первого порядка
. Условие минимума первого порядка 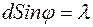 . Из рис. 4.2.1 видно:
. Из рис. 4.2.1 видно:  . Длина волны де Бройля для электрона
. Длина волны де Бройля для электрона  . Здесь
. Здесь  – масса электрона,
– масса электрона, 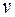 – его скорость. Ускоряемый разностью потенциалов электрон приобретает кинетическую энергию
– его скорость. Ускоряемый разностью потенциалов электрон приобретает кинетическую энергию 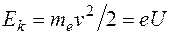 , откуда находим:
, откуда находим: 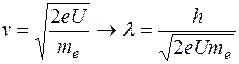 . Используя это, находим:
. Используя это, находим: 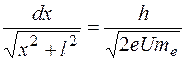 . Отсюда
. Отсюда .
.


