
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Третий закон Ньютона. Законы сил.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Общее свойство всех сил взаимодействия постулировано в 3-ем законе Ньютона: силы взаимодействия 2-ух мат точек в ИСО всегда равны по модулю и направлены в противоположные стороны вдоль прямой, соединяющей эти точки:
5. Преобразования координат Г. Галилея. Принцип относительности Г. Галилея.
Принцип относительности Галилея: все мех явления в разных ИСО будут протекать одинаково.
6. Сила тяжести и вес тела. Закон Гука. Модули упругости, коэффициент Пуассона. Согласно закону всемирного тяготения Ньютона, все тела во Вселенной, обладающие массой, притягиваются друг к другу с силой, называемой гравитационной. Эта сила прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними: F = G*m1*m2/r² где G - гравитационная постоянная Сила тяжести F= m*g является одной из составляющих силы гравитационного притяжения тела массы т к Земле (или другой планете). Другой составляющей является центростремительная сила, создающая центростремительное ускорение телу при его вращении вместе с Землей. Эта составляющая много меньше силы тяжести, поэтому ею часто пренебрегают и считают, что сила тяжести приблизительно равна силе гравитационного притяжения. Исходя изравенства силы тяжести на любой высоте над поверхностью планеты и силы гравитационного притяжения можно рассчитать ускорение свободного падения тела на поверхности Земли: g = G*Mз/R² = 9,8 м/с2, где Мз — масса Земли, R — радиус Земли. Весом тела (Р) называют силу, с которой тело вследствие зго притяжения к Земле действует на горизонтальную опору или подвес. Если тело находится в покое на горизонтальной поверхности или равномерно движется вместе с нею, то вес тела, который численно равен силе реакции опоры, совпадает с величиной силы тяжести, т. е. Р = тg. Если же тело вместе с опорой дви-сется равноускоренно в вертикальном направлении, то вес тела отличается от силы тяжести. Когда вектор ускорения а противоположно направлен с ускорением свободного падения g, то возникает состояние перегрузки, при котором Р > тg. В случае совпадения направлений а и gвес тела становится меньше силы тяжести. Если тело вместе с опорой двигаются с ускорением а =g, то вес оказывается равным нулю. Состояние с нулевым весом называют невесомостью. Зако́н Гу́ка — уравнение теории упругости, связывающее напряжение и деформацию упругой среды. Открыт в 1660 году английским учёным Робертом Гуком (Хуком) (англ. Robert Hooke). Поскольку закон Гука записывается для малых напряжений и деформаций, он имеет вид простой пропорциональности. В словесной форме закон звучит следующим образом: Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации Для тонкого растяжимого стержня закон Гука имеет вид:
Здесь Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения
Величина Если ввести относительное удлинение
то закон Гука в относительных единицах запишется как
В такой форме он справедлив для любых малых объёмов вещества. Также при расчёте прямых стержней применяют запись закона Гука в относительной форме
Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях. Коэффициент Пуассона (обозначается как При приложении к телу растягивающего усилия оно начинает удлиняться (то есть продольная длина увеличивается), а поперечное сечение уменьшается. Коэффициент Пуассона показывает, во сколько раз продольная деформация деформируемого тела больше поперечной деформации, при его растяжении или сжатии. Для абсолютно хрупкого материала коэффициент Пуассона равен 0, для абсолютно несжимаемого — 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, для резины он примерно равен 0,5. 7. Сухое и вязкое трение. Формула Ньютона. Виды сухого трения: покоя, скольжения, качения.
Внешнее трение — механическое сопротивление, возникающее в плоскости касаний двух соприкасающихся, прижатых друг к другу тел при их относительном перемещении. Сила сопротивления, направленная противоположно относительному перемещению тела, называется силой трения, действующей на это тело. На величину внешнего трения влияют: нагрузка, скорость перемещения тел, шероховатость их поверхностей, температура, наличие смазки. Наибольшее значение сила трения имеет в момент «трогания» тела с места. Различают трение покоя, трение скольжения, трение качения и вязкое трение. Сила трения качения обычно значительно меньше силы трения скольжения, а скольжения меньше силы трения покоя. Сила трения покоя — сила, возникающая между телами при отсутствии относительного движения тел. Сила трения скольжения — сила, возникающая при движении тел друг по другу. Сила трения качения — сила, возникающая при вращательном движении одного тела по другому. Вязкая сила трения — сила, возникающая в газах и жидкостях (сила сопротивления). Импульс (от лат. impulsus — удар, толчок) — мера механического движения. В механики различают два импульса: импульс силы и импульс массы. Закон сохранения импульса — закон механики, в соответствии с которым: векторная сумма импульсов тел в замкнутой системе остается постоянной при любых взаимодействиях этих тел между собой и может только перераспределяться между частями системы. Второй закон Ньютона в импульсной форме: из второго закона Ньютона: 8. Закон Всемирного тяготения. Напряженность, работа, потенциал гравитационного поля. В рамках классической механики гравитационное взаимодействие описывается законом всемирного тяготения. Этот закон был открыт Ньютоном в 1666 г.. Он гласит, что сила гравитационного притяжения между двумя материальными точками массы
Здесь Напряженность 9. Космические скорости. Космическая скорость (первая v 1, вторая v 2, третья v 3 и четвёртая v 4) — это минимальная скорость, при которой какое-либо тело в свободном движении с поверхности небесного тела сможет: § v 1 (круговая скорость) — стать спутником небесного тела (то есть вращаться по круговой орбите вокруг НТ на нулевой или пренебрежимо малой высоте относительно поверхности); § v 2 (параболическая скорость, скорость убегания) — преодолеть гравитационное притяжение небесного тела и уйти на бесконечность; § v 3 — покинуть звёздную систему, преодолев притяжение звезды; § v 4 — покинуть галактику. § Космические скорости. § Первая космическая скорость — скорость, которую необходимо придать баллистическому снаряду, пренебрегая сопротивлением атмосферы и вращением планеты, чтобы поместить его на круговую орбиту с радиусом равном радиусу планеты. Иными словами, первая космическая скорость — это скорость, с которой надо бросить камень в горизонтальном направлении, чтобы он больше не упал на Землю. Для вычисления первой космической скорости необходимо рассмотреть равенство центробежной силы и силы тяготения действующих на снаряд на круговой орбите. § § § где m — масса снаряда, M — масса планеты, G — гравитационная постоянная (6,67259·10−11 м³·кг−1·с−2), § § Первую космическую скорость можно определить через ускорение свободного падения — так как g = GM/R², то § § Первой космической скорости недоста точно для того, чтобы тело могло выйти из сферы земного притяжения. Необходимая для этого скорость называется второй кос мической. Второй космической (или пара болической) скоростью v2 называют ту наименьшую скорость, которую надо со общить телу, чтобы оно могло преодолеть притяжение Земли и превратиться в спут ник Солнца, т. е. чтобы его орбита в поле тяготения Земли стала параболической. Для того чтобы тело (при отсутствии со противления среды) могло преодолеть земное притяжение и уйти в космическое пространство, необходимо, чтобы его кине тическая энергия была равна работе, совершаемой против сил тяготения: § § Между первой и второй космическими скоростями существует простое соотношение: § § Для того чтобы покинуть пределы солнечной системы, тело должно преодолеть, кроме сил притяжения к земле, также и силы притяжения к Солнцу. Необходимая для этого скорость запуска тела с поверхности Земли называется третьей космической скоростью V3. Скорость V3 зависит от направления запуска. При запуске в направлении орбитального движения Земли эта скорость минимальна и составляет около 17 км/с. При запуске в направлении, противоположном направлению движения Земли, V3 равняется примерно 73 км/с. 10. Неинерциальные системы отсчета. Сила инерции. Сила Кориолиса и ее проявление в природе и технике.
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 998; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.011 с.) |

 . Принцип дальнодействия: взаимодействие между телами распространяется в пространстве с б.б.скоростью. При скоростях << скорости света 2 и 3 законы Ньютона выполняются с большой точностью.
. Принцип дальнодействия: взаимодействие между телами распространяется в пространстве с б.б.скоростью. При скоростях << скорости света 2 и 3 законы Ньютона выполняются с большой точностью.  подтверждает ЗСИ в ИСО. Парность взаимодействия: сила, с кот взаимодействуют 2 тела (мат точки), зависит только от их относительного положения и относительной скорости движения.
подтверждает ЗСИ в ИСО. Парность взаимодействия: сила, с кот взаимодействуют 2 тела (мат точки), зависит только от их относительного положения и относительной скорости движения.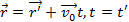 . Преобразования Галилея:
. Преобразования Галилея:  . Дифф. Преобразования по вр: классический закон преобразования скорости точки при переходе от одной ИСО к др:
. Дифф. Преобразования по вр: классический закон преобразования скорости точки при переходе от одной ИСО к др: 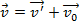 . Поэтому вектор скорости, кинетическая эн и импульс точки не являются инвариантными величинами в разных ИСО.
. Поэтому вектор скорости, кинетическая эн и импульс точки не являются инвариантными величинами в разных ИСО. 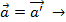 ускорение тела одинаково во всех ИСО. Т.к. во всех ИСО масса постоянна, тогда:
ускорение тела одинаково во всех ИСО. Т.к. во всех ИСО масса постоянна, тогда: 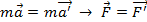 . Вывод: законы Ньютона и механики инвариантны (неизменны) по отношению к преобразованиям Галилея.
. Вывод: законы Ньютона и механики инвариантны (неизменны) по отношению к преобразованиям Галилея.
 — сила натяжения стержня,
— сила натяжения стержня,  — абсолютное удлинение (сжатие) стержня, а
— абсолютное удлинение (сжатие) стержня, а  называется коэффициентом упругости (или жёсткости).
называется коэффициентом упругости (или жёсткости). и длины
и длины 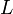 ) явно, записав коэффициент упругости как
) явно, записав коэффициент упругости как
 называется Модулем упругости первого рода или модулем Юнга и является механической характеристикой материала.
называется Модулем упругости первого рода или модулем Юнга и является механической характеристикой материала. и нормальное напряжение в поперечном сечении
и нормальное напряжение в поперечном сечении


 или
или 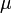 ) характеризует упругие свойства материала.
) характеризует упругие свойства материала. получаем
получаем 
 и
и  , разделёнными расстоянием
, разделёнными расстоянием  , пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними — то есть:
, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними — то есть:
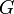 — гравитационная постоянная, равная
— гравитационная постоянная, равная  м³/(кг с²).
м³/(кг с²). гравитационного поля – векторная характеристика поля:
гравитационного поля – векторная характеристика поля:  .
.  , связанный с
, связанный с  . Для грав поля, создаваемого мат точкой с массой М, находящейся в начале координат, напряженность равна:
. Для грав поля, создаваемого мат точкой с массой М, находящейся в начале координат, напряженность равна:  ,
,  – радиус-вектор точки поля, в кот определяется
– радиус-вектор точки поля, в кот определяется  :
:  . Потенциал гравитационного поля зависит от массы тела, создающего грав поле, и расстоянием от центра данного тела до нек точки поля:
. Потенциал гравитационного поля зависит от массы тела, создающего грав поле, и расстоянием от центра данного тела до нек точки поля:  . Потенциальная эн тела вблизи пов Земли:
. Потенциальная эн тела вблизи пов Земли:  , где постоянная С на пов Земли принимается равной 0. Тогда
, где постоянная С на пов Земли принимается равной 0. Тогда  .
.
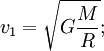
 — первая космическая скорость, R — радиус планеты. Подставляя численные значения (для Земли, M = 5,97·1024 кг, R = 6 378 000 м), найдем
— первая космическая скорость, R — радиус планеты. Подставляя численные значения (для Земли, M = 5,97·1024 кг, R = 6 378 000 м), найдем 7,9 км/с
7,9 км/с .
.




