
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложение гармонических колебаний одного направления.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 1. Сложение двух колебаний одного направления (сонаправленных колебаний)
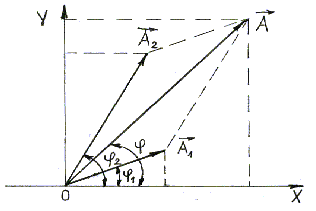
можно провести с помощью метода векторных диаграмм (Рисунок 9) вместо сложения двух уравнений. На Рисунке 2.1 показаны векторы амплитуд А 1(t) и А 2(t) складываемых колебаний в произвольный момент времени t, когда фазы этих колебаний соответственно равны Результирующему колебанию
Рисунок 2.1 – Сложение сонаправленных колебаний. Величина вектора А (t) может быть найдена по теореме косинусов:
Фаза результирующего колебания задается формулой:
Если частоты складываемых колебаний ω1 и ω2 не равны, то и фаза φ(t), и амплитуда А (t) результирующего колебания будут изменяться с течением времени. Складываемые колебания называются некогерентными в этом случае. 2. Два гармонических колебания x1 и x2 называются когерентными, если разность их фаз не зависит от времени:
Но так как Амплитуда результирующего колебания, полученного при сложении сонаправленных колебаний с равными частотами (когерентных колебаний) равна:
Начальную фазу результирующего колебания легко найти, если спроектировать векторы А 1 и А 2 на координатные оси ОХ и ОУ (см. Рисунок 9):
Итак, результирующее колебание, полученное при сложении двух гармонических сонаправленных колебаний с равными частотами, также является гармоническим колебанием 3. Исследуем зависимость амплитуды результирующего колебания от разности начальных фаз складываемых колебаний. Если (n = 0, 1, 2…), то Если 4. Сложение сонаправленных колебаний с неравными, но близкими частотами. Частоты складываемых колебаний не равны Примером сложения сонаправленных колебаний с близкими частотами является движение горизонтального пружинного маятника, жесткость пружин которого немного различна k1 и k2. Пусть амплитуды складываемых колебаний одинаковы
Результирующее колебание описывается уравнением:
Получившееся уравнение колебаний зависит от произведения двух гармонических функций: одна – с частотой
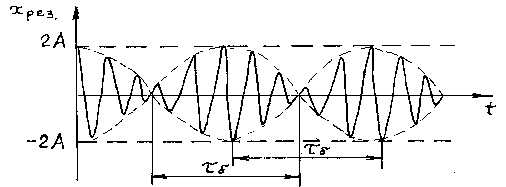
Абсолютное значение косинуса взято потому, что амплитуда – величина положительная. Характер зависимости хрез.при биениях показан на Рисунке 2.2.
Рисунок 2.2 – Зависимость смещения от времени при биениях. Амплитуда биений медленно меняется с частотой
Величина Величина
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 616; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.007 с.) |


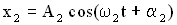
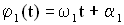 и
и 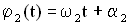 . Сложение колебаний сводится к определению
. Сложение колебаний сводится к определению 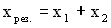 . Воспользуемся тем фактом, что на векторной диаграмме сумма проекций складываемых векторов равна проекции векторной суммы этих векторов.
. Воспользуемся тем фактом, что на векторной диаграмме сумма проекций складываемых векторов равна проекции векторной суммы этих векторов. и фаза
и фаза 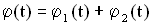 .
.
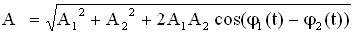 .
.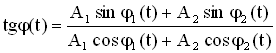 .
.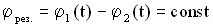 .
.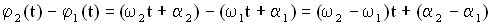 , то для выполнения условия когерентности двух этих колебаний должны быть равны их циклические частоты
, то для выполнения условия когерентности двух этих колебаний должны быть равны их циклические частоты 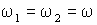 .
.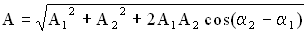 .
.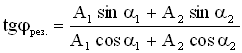 .
.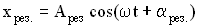 .
.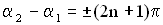 , где n – любое целое неотрицательное число
, где n – любое целое неотрицательное число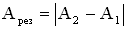 , т.е. результирующая амплитуда будет минимальной. Складываемые колебания в момент сложения находились в противофазе. При
, т.е. результирующая амплитуда будет минимальной. Складываемые колебания в момент сложения находились в противофазе. При 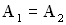 результирующая амплитуда равна нулю
результирующая амплитуда равна нулю 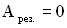 .
.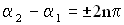 , то
, то 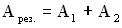 , т.е. результирующая амплитуда будет максимальной. В момент сложения складываемые колебания находились в одной фазе, т.е. были синфазны. Если амплитуды складываемых колебаний одинаковы
, т.е. результирующая амплитуда будет максимальной. В момент сложения складываемые колебания находились в одной фазе, т.е. были синфазны. Если амплитуды складываемых колебаний одинаковы 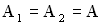 , то
, то 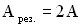 .
. , но разность частот
, но разность частот 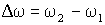 много меньше и ω1, и ω2. Условие близости складываемых частот записывается соотношениями
много меньше и ω1, и ω2. Условие близости складываемых частот записывается соотношениями 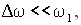
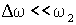 .
.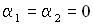 . Тогда уравнения складываемых колебаний имеют вид:
. Тогда уравнения складываемых колебаний имеют вид: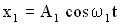 ,
, 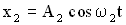 .
.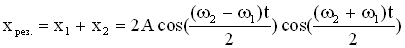 .
.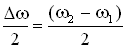 , другая – с частотой
, другая – с частотой 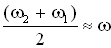 , где ω близка к частотам складываемых колебаний (ω1 или ω2). Результирующее колебание можно рассматривать как гармоническое колебание с изменяющейся по гармоническому закону амплитудой. Такой колебательный процесс называется биениями. Строго говоря, результирующее колебание в общем случае не является гармоническим колебанием.
, где ω близка к частотам складываемых колебаний (ω1 или ω2). Результирующее колебание можно рассматривать как гармоническое колебание с изменяющейся по гармоническому закону амплитудой. Такой колебательный процесс называется биениями. Строго говоря, результирующее колебание в общем случае не является гармоническим колебанием.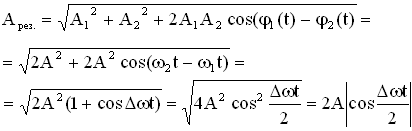
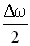 . Абсолютное значение косинуса повторяется, если его аргумент изменяется на π, значит и значение результирующей амплитуды повторится через промежуток времени τб, называемый периодом биений (см. Рисунок 12). Величину периода биений можно определить из следующего соотношения:
. Абсолютное значение косинуса повторяется, если его аргумент изменяется на π, значит и значение результирующей амплитуды повторится через промежуток времени τб, называемый периодом биений (см. Рисунок 12). Величину периода биений можно определить из следующего соотношения: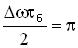 .
.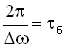 - период биений.
- период биений.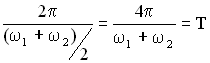 есть период результирующего колебания (Рисунок 2.4).
есть период результирующего колебания (Рисунок 2.4).


