Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование одноконтурных линейных систем автоматического регулированияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: исследовать переходные процессы в линейных одноконтурных системах. Общие положения
САУ (САР) называют систему, включающую в себя управляющее устройство (регулятор) и управляемый объект. Принцип построения систем автоматического управления могут быть разные: по возмущающему воздействию – разомкнутые системы; по отклонению (принцип обратной связи) – замкнутые системы; комбинированные – совмещающие оба этих принципа. В зависимости от цели управления их делят на: - системы стабилизации – задающее воздействие постоянно - системы программного управления – задающее воздействие изменяется по программе - следящие системы – задающее воздействие изменяется по неизвестному закону Системы стабилизации и программного управления могут быть как замкнутыми, так и разомкнутыми. Следящие системы используют в основном принцип обратной связи. Задача системы автоматического управления сводится к обеспечению соотношения САР должна вести себя по отношению к задающим и возмущающим воздействиям различным образом. Если g(t) должна определять изменение регулируемой переменной, то f(t) должна наименьшим образом влиять на изменение регулируемых переменных. Внешние воздействия, приложенные к системе, приводят к тому, что требуемые и действительные значения регулируемой величины отличаются, что и называют ошибкой системы автоматического регулирования. Отклонением регулируемой величины называют разность между значением регулируемой величины в данный момент времени и заданным ее значением:
где Y(t) – регулируемая величина; E(t) – сигнал ошибки. Воздействие, приложенное к сравнивающему элементу системы регулирования, называют входным сигналом системы. Регулируемой величиной называют сигнал на выходе системы. САР часто называют системами с обратной связью. Это объясняется тем, что в них имеется не только прямая связь между входом (задающим воздействием) и выходом (регулируемой переменной), но и обратная связь между выходом и входом, служащая для сравнения этих величин. Сигнал, который поступает с выхода системы на ее вход, называют сигналом главной обратной связи. Главная обратная связь всегда отрицательна.
Введение обратной связи создает систему, которая слабо реагирует на возмущающее воздействие и подчиняется, главным образом, задающему воздействию, т.е. замкнутая система регулирования по существу представляет собой фильтр, который достаточно точно передает g(t) и подавляет f(t) – возмущающее воздействие. САР с одной регулируемой величиной, имеющие только одну главную обратную связь, и не имеющие местных обратных связей, называют одноконтурными. САР подразделяют на статические и астатические в зависимости от того, имеют они или нет ошибку в установившемся состоянии при определенного рода воздействиях. Статическое регулирование – при котором регулируемая величина при разных, но постоянных внешних воздействиях на объект по окончании переходного процесса принимает различные значения, зависящие от величины внешнего воздействия. Контур регулирования должен состоять из статических звеньев, осуществляющих зависимость y=f(x). Астатическое регулирование – когда при различных постоянных значениях внешнего воздействия на объект отклонение регулируемой величины от требуемого значения по окончании переходного процесса становится равным нулю. В контур регулирования должно быть введено астатическое звено (интегрирующее звено В системах, статических по отношению к задающему воздействию, постоянным значениям этого воздействия соответствует постоянная ошибка системы, величина которой зависит от величины g(t). В астатических системах после окончания переходного процесса ошибка равна нулю. В теории автоматического регулирования широкое применение получил способ математического описания, основанный на использовании передаточных функций. По структурным схемам определяют передаточную функцию замкнутых систем относительно входного сигнала, ошибки и возмущения. Передаточной функцией линейной стационарной динамической системы называют отношение преобразования Лапласа Y(p) величины y(t) на выходе системы к преобразованию Лапласа X(p) воздействия x(t) на её входе при нулевых начальных условиях. Передаточная функция полностью характеризует динамические свойства системы. Зная передаточную функцию и вид воздействия, можно определить переходной процесс на выходе системы.
Поведение САР существенно зависит от величины и характера воздействий на систему. В виде типового воздействия при анализе динамики САР часто выбирают ступенчатое воздействие или единичный скачок. Такого рода воздействию соответствует, например, сброс или увеличение нагрузки в системах регулирования скорости электродвигателей. Переходные процессы в системах при скачкообразном входном сигнале можно разделить на следующие типы: 1) колебательный процесс, который характеризуется несколькими значениями перерегулирования; 2) малоколебательный процесс, который характеризуется одним перерегулированием; 3) монотонный процесс, который характеризуется тем, что скорость изменения регулируемой величины не меняет знака в течении всего переходного процесса; 4) апериодический процесс (процесс без перерегулирования), который характеризуется тем, что отклонение регулируемой величины остается в переходном процессе меньше установившегося значения (не меняет знака). Рассмотрим основные показатели качества системы автоматического регулирования, которые определяются по переходной характеристике (рисунок 5.2). В точке Под максимальным перерегулированием
где
Второй показатель качества позволяет оценить быстродействие системы автоматического регулирования и называется временем регулирования (протекания переходного процесса)
Рисунок 5.1 – Типы переходных процессов
Рисунок 5.2 – Определение показателей качества по переходной характеристике
Третий показатель качества характеризует число колебаний Наряду с этими основными показателями качества существуют и другие характеристики: Собственная частота колебаний системы:
где Логарифмический декремент затухания системы
где Максимальная скорость отработки регулируемой величины
Порядок выполнения лабораторной работы
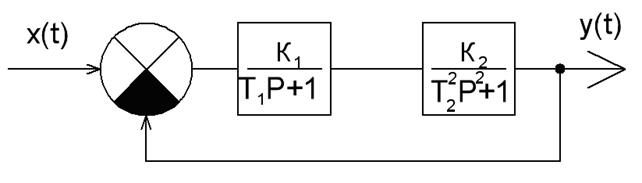
1.1 Для системы, структурная схема которой представлена на рисунке 5.3, определить характеристики системы (порядок системы, структурно устойчива или нет, статическая или астатическая), записать передаточные функции 1.2 При выборе постоянных времени и коэффициентов передачи учитывать следующие рекомендации:
Рисунок 5.3
1.3 Собрать схему в программе VisSim, исследовать переходной процесс в системе, подавая на вход ступенчатый сигнал. 1.4 По полученным графикам произвести измерение 1.5 Сделать выводы о влиянии коэффициентов схемы на характер переходного процесса.
2.1 Для системы, структурная схема которой представлена на рисунке 5.4, выполнить исследование по п.1.1-1.5.
Рисунок 5.4
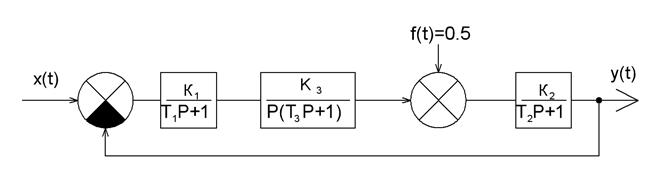
3.1 Для системы, структурная схема которой представлена на рисунке 5.5, определить характеристики системы (порядок системы, структурно устойчива или нет, статическая или астатическая по задающему воздействию и по возмущению), записать передаточные функции 3.2 Записать выражение для вычисления ошибки (по задающему воздействию и по возмущению) и вычислить ошибку, используя теорему о предельных переходах. 3.3 Собрать схему в программе VisSim, исследовать переходной процесс в системе, подавая на вход системы и вход возмущения ступенчатый сигнал.
Рисунок 5.5
3.4 Сравнить значения установившейся ошибки 3.5 Изменяя величину
4.1 Для системы, структурная схема которой представлена на рисунке 5.6, выполнить исследование по п.3.1-3.5.
Рисунок 5.6
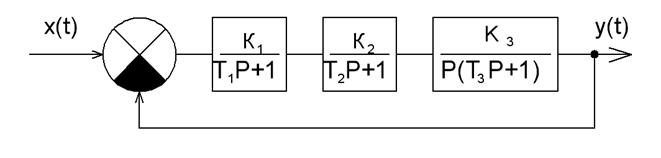
5.1 Для системы, представленной на рисунке 5.7 записать передаточные функции
Рисунок 5.7
5.2 Собрать схему в программе VisSim, исследовать переходной процесс в системе, подавая на вход ступенчатый сигнал. Установить, возможно ли изменением параметров добиться устойчивости системы.
Содержание отчёта
1. Схемы исследования и результаты исследования. 2. Передаточные функции, характеристическое уравнение, условие устойчивости, характеристики систем.
Контрольные вопросы
1. Что такое передаточные функции системы: разомкнутой по главной обратной связи, замкнутой, по ошибке, по возмущению. Как их записать по структуре системы?
2. Что такое устойчивость системы? 3. Что такое структурная устойчивость системы? Как ее определить? 4. Что такое статическое и астатическое регулирование? Как определить астатизм системы по задающему воздействию и по возмущению? 5. Что такое время регулирования, перерегулирование, статическая ошибка, как они определяются? Лабораторная работа № 6
|
||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 720; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.38.165 (0.013 с.) |

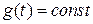 ;
;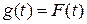 ;
;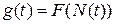 .
. , т.е. воспроизвести с требуемой точностью задающее воздействие.
, т.е. воспроизвести с требуемой точностью задающее воздействие.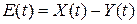 ,
, – задающее воздействие;
– задающее воздействие; ), которое находится в состоянии безразличного равновесия при отсутствии на него внешнего воздействия и выходит из равновесия при наличии воздействия.
), которое находится в состоянии безразличного равновесия при отсутствии на него внешнего воздействия и выходит из равновесия при наличии воздействия. переходного процесса, соответствующей времени
переходного процесса, соответствующей времени 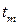 , имеет место максимальное отклонение регулируемой величины
, имеет место максимальное отклонение регулируемой величины 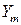 .
.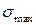 понимается величина максимального отклонения регулируемой величины от установившегося значения, выраженное в процентах:
понимается величина максимального отклонения регулируемой величины от установившегося значения, выраженное в процентах: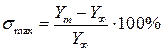 ,
,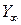 соответствует установившемуся значению регулируемой величины, т.е.
соответствует установившемуся значению регулируемой величины, т.е.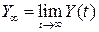 .
. .
. 
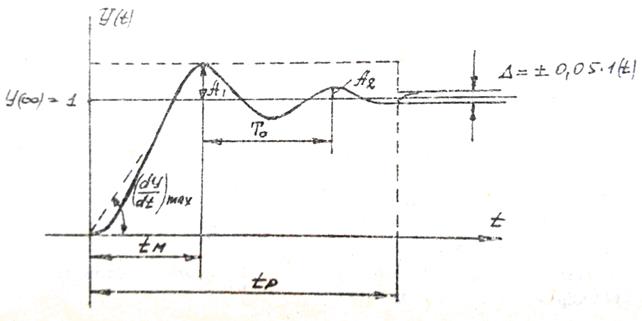
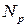 регулируемой величины
регулируемой величины 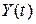 в течение времени переходного процесса
в течение времени переходного процесса 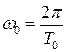 ,
,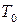 – период собственных колебаний системы.
– период собственных колебаний системы. , характеризующий быстроту затухания колебательного процесса:
, характеризующий быстроту затухания колебательного процесса: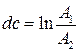 ,
, – две амплитуды для рядом расположенных экстремумов кривой переходного процесса. Чем больше
– две амплитуды для рядом расположенных экстремумов кривой переходного процесса. Чем больше 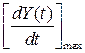 .
. и
и 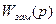 , характеристическое уравнение, выражения для коэффициентов характеристического уравнения, записать условие устойчивости.
, характеристическое уравнение, выражения для коэффициентов характеристического уравнения, записать условие устойчивости. ,
,  . Выбрав параметры звеньев, проверить, выполняется ли условие устойчивости; если нет – требуется изменить коэффициент усиления системы или увеличить кратность постоянных времени.
. Выбрав параметры звеньев, проверить, выполняется ли условие устойчивости; если нет – требуется изменить коэффициент усиления системы или увеличить кратность постоянных времени.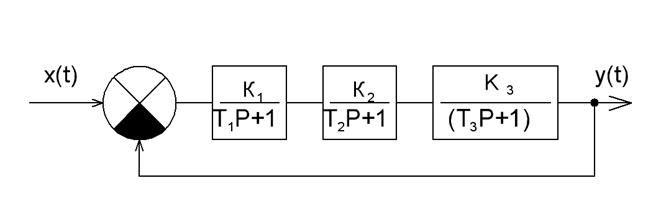
 ,
, 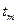 ,
, 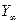 ,
, 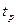 ,
, 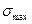 ,
, 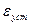 . Рассчитать, используя теорему о пределах
. Рассчитать, используя теорему о пределах 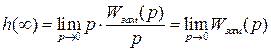 .
.
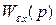 и
и 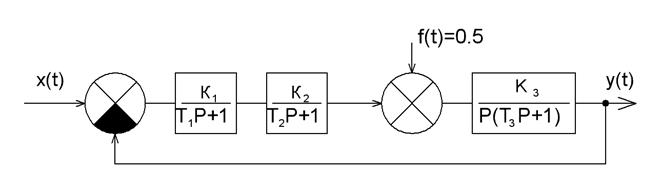
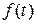 и коэффициент усиления системы
и коэффициент усиления системы 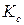 , сделать выводы.
, сделать выводы.