
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория Автоматического Управления (ТАУ)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теория Автоматического Управления (ТАУ) Лекция 1 Основные термины и определения ТАУ Основные понятия
Для поддержания качества выпускаемой продукции, все показатели технологического режима величины необходимо поддерживать постоянными или изменять по определенному закону. Данный процесс называется управлением. В общем случае управление – это динамический процесс перевода системы из текущего состояния в заданное. Управление процессами вручную не всегда представляется возможным, поскольку в системах управления человек-операторов становится «слабым звеном» по быстродействию, силовым возможностям, информационной избыточности или недостаточности и вообще потому что он - человек.. Автоматическое управление- это управление, осуществляемое без участия человека. Под разработкой автоматических систем регулирования понимается, во-первых, выбор соответствующих регуляторов, датчиков и исполнительных устройств, во-вторых, расчет параметров настроек этого оборудования. Теория автоматического управления (ТАУ) представляет собой математический инструмент для решения задач синтеза таких систем. 1. Определимся с основными понятиями. Физические величины, определяющие ход технологического процесса, называются параметрами технологического процесса. Например, температура, давление, расход, напряжение, состав и т.д. Параметр технологического процесса, который необходимо поддерживать постоянным или изменять по определенному закону, называется регулируемой величиной или регулируемым параметром. Значение регулируемой величины в данный момент времени называется мгновенным значением. Значение регулируемой величины, полученное в данный момент времени на основании измерений, называется ее измеренным значением.
Объект управления (объект регулирования) – система, требуемый режим выходных параметров которой должен изменяться или поддерживаться управляющими воздействиями. Управление – формирование управляющих воздействий (чаще всего –энергетических потоков), обеспечивающих требуемый режим работы объекта управления (ОУ). Регулирование – частный вид управления, когда задачей является обеспечение постоянства какой-либо выходной величины ОУ.
Автоматическое управление – управление, осуществляемое без непосредственного участия человека. Входное воздействие (Х) – воздействие, подаваемое на вход системы или устройства. Выходное воздействие (Y) – воздействие, выдаваемое на выходе системы или устройства. Внешнее воздействие – воздействие внешней среды на систему. Структурная схема системы регулирования температуры изображена на рисунке 1.2.
Любая система управления (ручного, автоматического или автоматизированного) в обязательном порядке содержит четыре элемента (или четыре множества элементов), объединенных в замкнутый контур передачи воздействий (см. рисунок 1.6): - объект управления, - управляющая часть, - датчик (датчики), - исполнительное устройство (устройства).
Рисунок 1.2
Датчик (Д) – устройство или комплекс устройств, преобразующих измеряемый параметр технологического процесса в вид, удобный для дальнейшей передачи и использования. Как правило, технологические параметры неудобно или невозможно контролировать (наблюдать, выводить на пульт оператора и т.д.) напрямую без дополнительных технических средств. Например, температуру нельзя наблюдать визуально, контроль температуры тела возможен только в сравнении со степенью нагретости какого-либо другого тела. Чтобы контроль параметров стал возможен, используют разного рода датчики, которые преобразуют измеряемые параметры в показания на шкале прибора (показывающие датчики, например, ртутный термометр), в разность потенциалов (например, термопары) в сопротивление (термометры сопротивления), в давление). Датчик измеряет технологический параметр, преобразует его в другой вид энергии и передает управляющей части. Управляющая часть реализует алгоритмы управления. В автоматических системах управления этой частью является регулятор, для систем ручного управления – человек-оператор. В управляющей части генерируются управляющие воздействия на объект управления (например, решения на включение/выключение, изменения напряжения и т.д.). Для реализации управляющих воздействий служат исполнительные устройства (ИУ). Работа датчиков и исполнительных устройств в отличие от управляющей части заключается лишь в преобразовании энергии, изменения информации в них практически не происходит (если не считать погрешности). Поэтому при анализе и синтезе систем управления чаще эти части СУ опускают, считая их коэффициенты усиления равными «1». Наиболее часто в ТАУ при расчетах пользуются общей схемой одноконтурной АСР (см. рисунок 1.3).
На схеме приняты обозначения: x - задающее воздействие (задание), e = х - у - ошибка регулирования, u - управляющее воздействие, f - возмущающее воздействие (возмущение). Элемент
Рисунок 1.3
Определения: Выходное значение, параметр – технологические параметры, которые характеризует состояние обекта управления. Задающее воздействие (то же, что входное воздействие х) - воздействие, определяющее желаемый закон изменения регулируемой величины. Управляющее воздействие (u) - воздействие управляющего устройства на объект управления. Управляющее устройство (Р) - устройство, осуществляющее расчёт управляющего воздействия на объект управления с целью обеспечения требуемого режима работы. Возмущающее воздействие (f) – ненаблюдаемое и неизмеряемое случайное воздействие, которое изменяет состояние объекта управления и приводит к изменению выходных параметров. Отклонение, рассогласование (е = х - у) - разность между заданным (х) и действительным (у) значениями регулируемой величины. Регулятор (Р) - комплекс устройств, присоединяемых к регулируемому объекту и обеспечивающих автоматическое поддержание заданного значения его регулируемой величины или автоматическое изменение ее по определенному закону. Автоматическая система регулирования (АСР) (система автоматического регулирования САР) - автоматическая система с замкнутой цепью воздействия, в котором управление (u) вырабатывается в результате сравнения истинного значения у с заданным значением х. Дополнительная связь в структурной схеме АСР, направленная от выхода к входу рассматриваемого участка цепи воздействий, называется обратной связью (ОС). Обратная связь может быть отрицательной или положительной. Принцип функционирования одноконтурной АСР: регулятор производит постоянное сравнение текущего значения регулируемой величины у с заданным значением х, определяя ошибку е = х – у. Если текущее значение равно заданному, то регулятор не изменяет управляющее воздействие (АСР работает в установившемся режиме), в противном случае управляющее воздействие на объект u изменяется в соответствии с величиной ошибки. Чем больше ошибка регулирования (и дольше она наблюдается), тем больше изменение управляющего воздействия. Данная схема справедлива как для автоматического, так и для ручного управления. При ручном регулировании человек-оператор, наблюдая за показаниями датчиков, мысленно сравнивает их с заданными значениями, т.е. определяет величину ошибки регулирования и, исходя из этого, решает, какие действия предпринимать.
Классификация АСР 1 По назначению (по характеру изменения задания):
· стабилизирующая АСР - система, алгоритм функционирования которой содержит предписание поддерживать регулируемую величину на постоянном значении (x = const); · программная АСР - система, алгоритм функционирования которой содержит предписание изменять регулируемую величину в соответствии с заранее заданной функцией (x изменяется программно, например, как функция времени); · следящая АСР - система, алгоритм функционирования которой содержит предписание изменять регулируемую величину в зависимости от заранее неизвестной величины на входе АСР (x изменяется произвольно). 2 По количеству контуров: · одноконтурные - содержащие один контур регулирования (одну обратную связь по регулируемому параметру), · многоконтурные - содержащие несколько контуров регулирования (несколько обратных связей, например, по нескольким параметрам, по скорости/ускорению изменения параметра и т.д.). 3 По числу регулируемых величин: · одномерные - системы с одной регулируемой величиной, · многомерные - системы с несколькими регулируемыми величинами. Многомерные АСР в свою очередь подразделяются на системы: а) несвязанного регулирования, в которых регуляторы непосредственно не связаны и могут взаимодействовать только через общий для них объект управления; б) связанного регулирования, в которых регуляторы различных параметров одного и того же технологического процесса связаны между собой вне объекта регулирования. 4 По функциональному назначению: АСР температуры, давления, расхода, уровня, напряжения и т.д. 5 По характеру используемых для управления сигналов: · непрерывные, · дискретные (релейные, импульсные, цифровые). 6 По характеру математических соотношений: · линейные, для которых справедлив принцип суперпозиции; · нелинейные. Примечание - Если на вход объекта подается несколько входных воздействий, то реакция объекта на сумму входных воздействий равна сумме реакций объекта на каждое воздействие в отдельности:
где L - линейная функция (интегрирование, дифференцирование и т.д.). Данный принцип называется принципом суперпозиции (наложения). 7 По виду используемой для регулирования энергии: · пневматические, · гидравлические, · электрические, · механические и др.
Основные модели Работу системы управления можно описать словесно. Словесное описание помогает понять принцип действия системы, ее назначение, особенности функционирования и т.д. Однако, что самое главное, оно не дает количественных оценок качества управления, поэтому не пригодно для изучения характеристик систем и построения систем автоматизированного управления. В ТАУ используются формализованные математические методы описания свойств систем:
· статические характеристики, · временные характеристики, · дифференциальные уравнения, · передаточные функции, · частотные характеристики и др.
Установившийся режим - это режим, при котором расхождение между истинным значением регулируемой величины и ее заданным значением будет постоянным во времени.
Статические характеристики
yуст = j(х).
Статическую характеристику (см. рис. 2.2) часто изображают графически в виде кривой у(х). Линейным статическим элементом называется безинерционный элемент, обладающий линейной статической характеристикой: ууст = К*х + а0. Как видно, статическая характеристика элемента в данном случае имеет вид прямой с коэффициентом наклона К. Линейные статические характеристики, в отличие от нелинейных, более удобны для изучения благодаря своей простоте. Если модель объекта нелинейная, то обычно ее преобразуют к линейному виду путем линеаризации. САУ называется статической, если при постоянном входном воздействии ошибка управления е стремится к постоянному значению, зависящему от величины воздействия. САУ называется астатической, если при постоянном входном воздействии ошибка управления стремится к нулю вне зависимости от величины воздействия.
Временные характеристики Переход системы от одного установившегося режима к другому при каких-либо входных воздействиях называется переходным процессом. Переходные процессы могут изображаться графически в виде кривой y(t).
То есть переходный процесс характеризует динамические свойства системы, ее поведение. Следует различать динамические и статические характеристики, поскольку они строятся в разных координатах и характеризуют различные свойства системы. Зная набор динамических характеристик при различных входных воздействиях, можно построить статическую характеристику, но по статической характеристике восстановить динамику невозможно. Поскольку входные воздействия могут изменяться во времени, то и переходные характеристики будут каждый раз разные. Для простоты анализа систем входные воздействия приводят к одному из типовых видов сигналов (см. рисунок 2.4).
В зависимости от вида входного воздействия функция у(t) может иметь разное обозначение: Переходной характеристикой h(t) называется реакция объекта на единичное ступенчатое воздействие (сигнал) при нулевых начальных условиях, т.е. при х(0) = 0 и у(0) = 0.
Импульсной характеристикой w(t) называется реакция объекта на d-функцию при нулевых начальных условиях. При подаче на вход объекта синусоидального сигнала на выходе, как правило, в установившемся режиме получается также синусоидальный сигнал, но с другой амплитудой и фазой: y = Aвых*sin(w*t + j), где Aвых - амплитуда, w - частота сигнала, j - фаза. Частотной характеристикой (ЧХ, АФХ и др.) называется зависимость амплитуды и фазы выходного сигнала системы в установившемся режиме при приложении на входе гармонического воздействия. Дифференциальные уравнения. Известно, что любое движение, процессы математически можно описать в виде дифференциальных уравнений (ДУ). Любые процессы в АСР также можно описать дифференциальными уравнениями, которые определяют сущность происходящих в системе процессов независимо от ее конструкции и т.д. Решив ДУ, можно найти характер изменения регулируемой переменной в переходных и установившихся режимах при различных воздействиях на систему. Для упрощения задачи нахождения ДУ, описывающего работу АСР в целом, систему разбивают на ее отдельные элементы, переходные процессы в которых описываются достаточно простыми ДУ. Для каждого элемента структурной схемы необходимо составить ДУ, определяющее зависимость изменения выходной величины от входной. Так как выходная величина предыдущего элемента является входной для последующего, то, определив ДУ отдельных элементов, можно найти ДУ системы. Однако такой метод применим только в частных случаях. В большинстве случаев в реальных элементах системы связь между входной и выходной величинами является нелинейной и часто задается в графической форме. Поэтому, даже если ДУ системы и будет получено, оно будет нелинейным. А аналитическое решение нелинейных ДУ возможно далеко не всегда. Для решения этой проблемы учитывают, что в процессе регулирования отклонения всех изменяющихся величин от их установившихся значений малы, и поэтому возможна замена нелинейных ДУ приближенными линейными ДУ, то есть возможна линеаризация дифференциальных уравнений.
Графически линеаризацию некоторого уравнения от двух переменных F(х,у) = 0 в окрестности некоторой точки (х0, у0) можно представить как замену рассматриваемого участка кривой на касательную (см. рисунок 2.5), уравнение которой определяется по формуле
Данное уравнение называется уравнением в приращениях, поскольку значения х и у здесь заменены на приращения Dх = х - х0 и Dу = у - у0. Линеаризация ДУ происходит аналогично, отличие состоит только в том, что необходимо искать частные производные по производным ( Пример. Линеаризация нелинейного ДУ. 3xy - 4x2 + 1,5 Данное ДУ является нелинейным из-за наличия произведений переменных х и у. Линеаризируем его в окрестности точки с координатами х0 = 1, 3у0 - 4 + 0 = 0 + у0, откуда у0 = 2. Введем в рассмотрение функцию F = 3xy - 4x2 + 1,5x’y - 5y’ - y и определим все ее производные при заданных начальных условиях:
Теперь, используя полученные коэффициенты, можно записать окончательное линейное ДУ: -5.Dy’ + 2.Dy + 3.Dх’ - 2.Dх = 0. ¨ Линеаризация ДУ, заданного в явном виде относительно у, т.е. y = F(x) производится по формуле
то есть в данном случае нет необходимости искать производные по у.
Лекция 3. Преобразования Лапласа Исследование АСР существенно упрощается при использовании прикладных математических методов операционного исчисления, поскольку позволяет от решения ДУ перейти к решению алгебраических уравнений. Например, функционирование некоторой системы описывается ДУ вида
где х и у - входная и выходная величины. Если в данное уравнение вместо x(t) и y(t) подставить функции X(s) и Y(s) комплексного переменного s такие, что
то исходное ДУ при нулевых начальных условиях равносильно линейному алгебраическому уравнению a2 s2 Y(s) + a1 s Y(s) + a0 Y(s) = b1 X(s) + b0 X(s). Такой переход от ДУ к алгебраическому уравнению называется преобразованием Лапласа, формулы (3.2) соответственно формулами преобразования Лапласа, а полученное уравнение - операторным уравнением. Новые функции X(s) и Y(s) называются изображениями x(t) и y(t) по Лапласу, тогда как x(t) и y(t) являются оригиналами по отношению к X(s) и Y(s). Переход от одной модели к другой достаточно прост и заключается в замене знаков дифференциалов
Таблица 3.1 - Преобразования Лапласа
Таблица 3.2 - Формулы обратного преобразования Лапласа (дополнение)
Для обратного перехода от операторного уравнения к функциям от времени используется метод обратного преобразования Лапласа. Общая формула обратного преобразования Лапласа:
где f(t) - оригинал, F(jw) - изображение при s = jw, j - мнимая единица, w - частота. Эта формула достаточно сложна, поэтому были разработаны специальные таблицы (см. таблицы 3.1 и 3.2), в которые сведены наиболее часто встречающиеся функции F(s) и их оригиналы f(t). Они позволяют отказаться от прямого использования формулы (3.2). Более полные таблицы преобразований Лапласа можно найти в специальной литературе Некоторые теоремы преобразования Лапласа. Теорема 1. Теорема линейности. Изображение суммы функций равно сумме изображений, то есть, если f1 имеет изображение F1(s) (или более кратко f1 «F1(s)), f2 «F2(s) и т.д., то a1.f1 + a2.f2 + … + an.fn «a1.F1(s) + a2.F2(s) + … + an.Fn(s). Теорема 2. Теорема дифференцирования. Если f(t) имеет изображение F(s), то при нулевых начальных условиях (т.е. при f(0) = 0, f’(0) = 0 и т.д.) производные f(t) будут иметь изображения: f’(t) «s.F(s) – для первой производной, f ”(t) «s2.F(s) – для второй производной, f(n)(t) «sn.F(s) – для n-й производной. При ненулевых начальных условиях: f’(t) «s.F(s) – f(0) – для первой производной, f ”(t) «s2.F(s) – s.f(0) – f’(0) – для второй производной, f(n)(t) «sn.F(s) – sn-1.f(0) - sn-2.f’(0) - … - f(n-1)(0) – для n-й. Теорема 5. Теорема интегрирования.
Закон изменения выходного сигнала обычно является функцией, которую необходимо найти, а входной сигнал, как правило, известен. Некоторые типовые входные сигналы были рассмотрены в п. 2.3. Здесь приводятся их изображения: единичное ступенчатое воздействие имеет изображение X(s) = дельта-функция X(s) = 1, линейное воздействие X(s) =
Пример 1. Решение ДУ с использованием преобразований Лапласа.
Допустим, входной сигнал имеет форму единичного ступенчатого воздействия, т.е. x(t) = 1. Тогда изображение входного сигнала, согласно таблице 3.1, имеет вид X(s) = Производим преобразование исходного ДУ по Лапласу и подставляем X(s): s2×Y(s) + 5×s×Y(s) + 6×Y(s) = 2×s×X(s) + 12×X(s), s2×Y(s) + 5×s×Y(s) + 6×Y(s) = 2×s Y(s)×(s3 + 5s2 + 6s) = 2×s + 12. Определяется выражение для Y:
Оригинал полученной функции отсутствует в таблице оригиналов и изображений. Для решения задачи его поиска дробь разбивается на сумму простых дробей с учетом того, что знаменатель может быть представлен в виде s(s + 2)(s + 3):
Теперь, используя табличные функции (см. таблицы 3.1 и 3.2), определяется оригинал выходной функции: y(t) = 2 - 4.e-2t + 2.e-3t. ¨ При решении ДУ с использованием преобразований Лапласа часто встает промежуточная задача разбиения дроби на сумму простых дробей. Существуют два пути решения этой задачи: - путем решения системы уравнений относительно коэффициентов числителей, - путем расчета коэффициентов числителей по известным формулам. Общий алгоритм разбиения дроби на сумму простых дробей: шаг 1 – определяются корни знаменателя si (знаменатель дроби приравниватся к нулю и решается полученное уравнение относительно s); шаг 2 – каждому корню ставится в соответствие простая дробь вида шаг 3 – определяются коэффициенты Mi по одному из вариантов расчета. Первый вариант. Определение Mi с помощью системы уравнений. Все дроби приводятся к одному знаменателю, затем путем сравнения коэффициентов при равных степенях s числителя полученной дроби и числителя исходной определяется система из n уравнений, где n – степень знаменателя (количество корней si и коэффициентов Mi). Решение системы относительно Mi дает искомые коэффициенты. Пример 2. Декомпозиция дроби из предыдущего примера. В исходной дроби n = 3, поэтому решение уравнения s3 + 5s2 + 6s = 0 дает 3 корня: s0 = 0, s1 = -2 и s2 = -3, которым соответствуют знаменатели простых дробей вида s, (s – s1) = (s + 2) и (s – s2) = (s + 3). Исходная дробь декомпозируется на три дроби:
Далее дроби приводятся к общему знаменателю: = Сравнивая получившуюся дробь с исходной, можно составить систему из трех уравнений с тремя неизвестными (при 2-й степени s в исходной дроби стоит 0, при 1-й стоит 2, свободный член равен 12):
5.М0 + 3.М1 + 2.М2 = 2 à M1 = -4 6.М0 = 12 M2 = 2 Следовательно, дробь можно представить как сумму трех дробей:
Второй вариант. Определение коэффициентов Mi по формулам. Также как и в 1-м варианте необходимо найти корни знаменателя исходной дроби вида - Для нулевого корня si = 0 знаменатель исходной дроби можно записать в виде A(s) = s.A1(s); тогда коэффициент Mi можно определить как - Для ненулевого некратного корня (действительного или комплексного) si:
где A’(s) – производная знаменателя по s. Примечание - Комплексные корни при решении уравнений появляются комплексно-сопряженными парами вида si = ai ± j×wi, где ai – действительная часть корня, wi – мнимая часть, j – мнимая единица. Поэтому коэффициенты для этих корней также будут комплексно-сопряженными: Mi = ci ± di. То есть достаточно определить коэффициент только для одного корня, для парного корня он будет комплексно-сопряженным. - Для корня si кратности k исходная дробь может быть представлена в виде
данному корню соответствуют k дробей вида
коэффициенты которых определяются по формуле
Пример 3. Декомпозиция дроби. Рассматривается та же дробь, имеющая три корня: s0 = 0, s1 = -2 и s2 = -3. Для корня s0 = 0 имеем B(s) = 2.s + 12, A1(s) = s2 + 5s + 6,
Для корня s1 = -2 имеем A’(s) = 3.s2 + 10.s + 6 и
Для корня s2 = -3 имеем аналогично
Видно, что коэффициенты Mi, полученные разными методами, совпадают.¨
Пример 4. Случай обратного преобразования Лапласа при наличии комплексных корней. Изображение выходного сигнала имеет вид
Корни знаменателя включают нулевой корень, действительный и пару комплексных корней: s0 = 0; s1 = - 2,54; s2,3 = - 0,18 ± j*1,20. Изображение Y(s) разбивается на сумму четырех дробей:
Тогда оригинал y(t), согласно таблицам 1.1 и 1.2, имеет вид y(t) = y0(t) + y1(t) + y2,3(t) = M0 + где a и w - действительная и мнимая части пары комплексных корней s2,3, C и D – действительная и мнимая части пары коэффициентов М2 и М3. Для корня s0 = 0:
y0(t) = M0 = 0,85. Для корня s1 = -2,54:
y1(t) = Для корней s2,3 = -0,18 ± j*1,20:
y2,3(t) =2 е-0,18t [-0,34 cos(1,20 t) - 0,24 sin(1,20 t)]. В итоге получаем оригинал: y(t) = 0,85 – 0,18 е-2,54 t – 2 е-0,18 t [0,34 cos(1,20 t) + 0,24 sin(1,20 t)].¨ Примеры типовых звеньев Звеном системы называется ее элемент, обладающий определенными свойствами в динамическом отношении. Звенья систем регулирования могут иметь разную физическую природу (электрические, пневматические, механические и др. звенья), но описываться одинаковыми ДУ, а соотношение входных и выходных сигналов в звеньях описываться одинаковыми передаточными функциями. В ТАУ выделяют группу простейших звеньев, которые принято называть типовыми. Статические и динамические характеристики типовых звеньев изучены достаточно полно. Типовые звенья широко используются при определении динамических характеристик объектов управления. Например, зная переходную характеристику, построенную с помощью самопишущего прибора, часто можно определить, к какому типу звеньев относится объект управления, а следовательно, его передаточную функцию, дифференциальное уравнение и т.д., т.е. модель объекта. Типовые звенья Любое сложное звено может быть представлено как соединение простейших звеньев. К простейшим типовым звеньям относятся: · усилительное, · инерционное (апериодическое 1-го порядка), · интегрирующие (реальное и идеальное), · дифференцирующие (реальное и идеальное), · апериодическое 2-го порядка, · колебательное, · запаздывающее. 1) Усилительное звено.
Выходной сигнал такого звена в точности повторяет входной сигнал, усиленный в К раз (см. рисунок 4.1). у = K.x. При ступенчатом воздействии h(t) = K. Примерами таких звеньев являются: механические передачи, датчики, безинерционные усилители и др.
2) Интегрирующее. Идеальное интегрирующее. Выходная величина идеального интегрирующего звена пропорциональна интегралу входной величины:
При подаче на вход звена ступенчатого воздействия x(t) = 1 выходной сигнал постоянно возрастает (см. рисунок 4.2): h(t) = K.t. Это звено астатическое, т.е. не имеет установившегося режима. Примером такого звена может служить емкость, наполняемая жидкостью. Входной параметр – расход поступающей жидкости, выходной - уровень. Изначально емкость пуста и при отсутствии расхода уровень равен нулю, но если включить подачу жидкости, уровень начинает равномерно увеличиваться.
2.2) Реальное интегрирующее.
W(s) = Переходная характеристика в отличие от идеального звена является к
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 6998; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.187.85 (0.018 с.) |



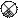 называется сумматором. Его действие заключается в суммировании поступающих к нему сигналов. Если какой-либо сектор сумматора зачернен, то сигнал, поступающий в данный сектор, берется со знаком «минус». Поэтому в данной схеме ошибка е определяется как разность между х и у.
называется сумматором. Его действие заключается в суммировании поступающих к нему сигналов. Если какой-либо сектор сумматора зачернен, то сигнал, поступающий в данный сектор, берется со знаком «минус». Поэтому в данной схеме ошибка е определяется как разность между х и у.
 L(х1 + х2) = L(х1) + L(х2),
L(х1 + х2) = L(х1) + L(х2), В любой из этих моделей система может быть представлена в виде звена, имеющего входные воздействия Х, возмущения F и выходные воздействия Y (см. рисунок 2.1). Под влиянием входных воздействий выходная величина может изменяться.
В любой из этих моделей система может быть представлена в виде звена, имеющего входные воздействия Х, возмущения F и выходные воздействия Y (см. рисунок 2.1). Под влиянием входных воздействий выходная величина может изменяться.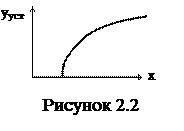 Статической характеристикой элемента называется зависимость установившихся значений выходной величины от значения величины на входе системы, т.е.
Статической характеристикой элемента называется зависимость установившихся значений выходной величины от значения величины на входе системы, т.е.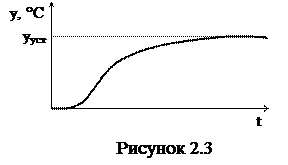 Например, процесс нагрева сушильного шкафа до установившегося значения может иметь вид, представленный на рисунке 2.3.
Например, процесс нагрева сушильного шкафа до установившегося значения может иметь вид, представленный на рисунке 2.3.
 Рассмотрим сущность процесса линеаризации на примере сушильного шкафа. Зависимость температуры объекта от подаваемого напряжения в большинстве случаев нелинейная и имеет вид, представленный на рисунке 2.5.
Рассмотрим сущность процесса линеаризации на примере сушильного шкафа. Зависимость температуры объекта от подаваемого напряжения в большинстве случаев нелинейная и имеет вид, представленный на рисунке 2.5. ,
, ,
,  ,
,  и т.д.). Итоговое уравнение в приращениях будет содержать приращения производных: Dх’ = х’ – х’0, Dх” = х” – х”0, …, Dy’ = y’ – y’0, Dy” = y” – y”0, и т.д.
и т.д.). Итоговое уравнение в приращениях будет содержать приращения производных: Dх’ = х’ – х’0, Dх” = х” – х”0, …, Dy’ = y’ – y’0, Dy” = y” – y”0, и т.д. y = 5
y = 5  + y
+ y = 0,
= 0,  = 0. Для определения недостающего начального условия у0 подставим данные значения в ДУ:
= 0. Для определения недостающего начального условия у0 подставим данные значения в ДУ: = (3у - 8х
= (3у - 8х  = 3*2 - 8*1 = -2,
= 3*2 - 8*1 = -2, = (3х + 1,5x’ - 1
= (3х + 1,5x’ - 1 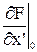 = (1,5у
= (1,5у  = -5.
= -5. ,
, , (3.1)
, (3.1) и
и  , (3.2)
, (3.2) на операторы sn, знаков интегралов
на операторы sn, знаков интегралов  на множители
на множители  , а самих x(t) и y(t) - изображениями X(s) и Y(s).
, а самих x(t) и y(t) - изображениями X(s) и Y(s).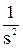
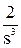





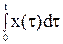


 , (3.3)
, (3.3) .
.
 .
. .
.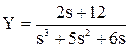 =
=  =
=  -
-  +
+  .
. , где Мi – неизвестный коэффициент; если имеет место кратный корень с кратностью k, то ему ставится в соответствие k дробей вида
, где Мi – неизвестный коэффициент; если имеет место кратный корень с кратностью k, то ему ставится в соответствие k дробей вида  ;
; +
+  +
+ 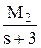 .
.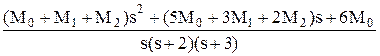 .
.
 М0 + М1 + М2 = 0 M0 = 2
М0 + М1 + М2 = 0 M0 = 2 . Для определения Mi существуют формулы для каждого вида корней:
. Для определения Mi существуют формулы для каждого вида корней: .
.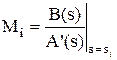 ,
,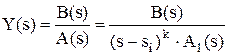 ;
;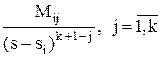 ,
,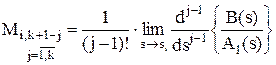 .
.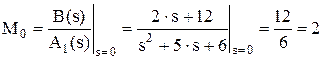 .
. .
. .
. .
. .
. + 2 еat [C . cos(w.t) - D . sin(w.t)],
+ 2 еat [C . cos(w.t) - D . sin(w.t)], ,
, ,
, ,
, ,
,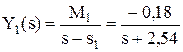 ,
, .
. ,
, ,
, ,
, Звено усиливает входной сигнал в К раз. Уравнение звена у = К*х, передаточная функция W(s) = К. Параметр К называется коэффициентом усиления.
Звено усиливает входной сигнал в К раз. Уравнение звена у = К*х, передаточная функция W(s) = К. Параметр К называется коэффициентом усиления.
 ; W(s) =
; W(s) = 
 Передаточная функция этого звена имеет вид
Передаточная функция этого звена имеет вид .
.


