
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория автоматического управления,Содержание книги Поиск на нашем сайте МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ «ВИТЕБСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ» ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ, РАЗДЕЛ «ЛИНЕЙНЫЕ СИСТЕМЫ»: Методические указания к выполнению лабораторных работ по курсу «Теория автоматического управления» для студентов специальности 1-53 01 01-05 «Автоматизация технологических процессов и производств (легкая промышленность)»
Витебск УДК 681.5
Теория автоматического управления, раздел «Линейные системы»: методические указания к выполнению лабораторных работ для студентов специальности 1-53 01 01-05 «Автоматизация технологических процессов и производств (легкая промышленность)»
Витебск: Министерство образования РБ, УО «ВГТУ», 2011.
Составители: к.т.н., доцент Иванова Л.В. ассистент Надёжная Н.Л.
Методические указания составлены в соответствии с программой курса «Теория автоматического управления»; содержат описание методики исследования линейных систем и структурные схемы для моделирования.
Одобрено на заседании кафедры «Автоматизация технологических процессов и производств» УО «ВГТУ» «____» ___________ 2011 г, протокол № ___.
Рецензент: к.т.н., доцент Попов Ю.В. Редактор: д.т.н., доцент Кузнецов А.А.
Рекомендовано к опубликованию редакционно-издательским советом УО «ВГТУ» «___»__________2011 г., протокол № ___.
Ответственный за выпуск Букин Ю.А.
Учреждение образования «Витебский государственный технологический университет» ________________________________________________________________ Подписано к печати__________ Формат___________. Уч.изд.л.__________ Печать ризографическая. Тираж _____ экз. Заказ № _____. Цена _______р.
Отпечатано на ризографе Учреждения образования «Витебский государственный технологический университет». Лицензия № 02330/0133005 от 1 апреля 2004 г. 210035, Витебск, Московский проспект, 72.
СОДЕРЖАНИЕ
Лабораторная работа №1 Знакомство с программой математического моделирования динамических систем VisSim, создание простейших моделей Цель работы: – знакомство с назначением, интерфейсом, принципами построения моделей и важными блоками (виртуальными моделями реальных устройств и их элементов) программы VisSim, а также приобретение навыков создания простейших моделей.
Общие положения
Основные сведения о работе в программе VisSim
Общие сведения о моделировании и назначение программы VisSim Моделирование технических объектов и систем проводится для того, чтобы определить свойства и характеристики проектируемых систем еще до их изготовления и при необходимости скорректировать, уточнить их структуру и параметры. Это позволяет получить проект работоспособной системы, которую не придется существенно дорабатывать тогда, когда она будет изготовлена. Таким образом, моделирование сокращает и удешевляет процесс проектирования и реализации систем и объектов. Кроме того, на модели системы можно проверить ее поведение в таких условиях и режимах, для которых система не предназначена, с тем, чтобы знать, как она себя поведет и к каким последствиям это приведет. Очевидно, что такие эксперименты на реальной системе могут быть не только дороги, но и небезопасны, в то время как моделирование позволяет получить нужную информацию о процессе или системе без лишних затрат и, главное, без негативных последствий. Программа VisSim предназначена для построения, исследования и оптимизации виртуальных моделей физических и технических объектов, в том числе и систем управления. VisSim это аббревиатура выражения Visual Simulator - визуальная, воспринимаемая зрением, среда и средство моделирования. Программа VisSim, разработана и развивается компанией Visual Solutions (USA). Эта программа - мощное, удобное в использовании, компактное и эффективное средство моделирования физических и технических объектов, систем и их элементов. При описании и последующем построении модели в среде VisSim нет необходимости записывать и решать дифференциальные уравнения, программа это сделает сама по предложенной ей исследователем структуре системы и параметрам ее элементов. Результаты решения выводятся в наглядной графической форме. Специалисты, владеющие программированием, могут создавать собственные блоки, дополняя ими библиотеку стандартных блоков VisSim. Для использования в учебных целях компанией Visual Solution Inc. бесплатно распространяется студенческая версия программы VisSim. Данная версия является полнофункциональной, но в ней отсутствуют файлы помощи и примеры. Принципы построения моделей в VisSim
Исходными данными для построения модели в VisSim являются структурно-функциональная схема моделируемой системы, процесса или объекта и описывающие их дифференциально-алгебраические уравнения. Вместо таких уравнений могут быть заданы операторы или функции, характеризующие отдельные элементы моделируемой системы, например, передаточные функции для линейных элементов и статические характеристики для нелинейных элементов. Реальные системы и объекты состоят из отдельных, связанных и взаимодействующих друг с другом элементов. И для всей системы в целом, и для отдельных ее, должным образом выбранных элементов, можно указать место приложения воздействия, которое можно назвать входом, и место их реакции (отклика) на входное воздействие, называемое выходом. И воздействие, и реакция – это некоторые физические величины, являющиеся функциями времени. Модели систем и объектов в программе VisSim строятся из отдельных элементов – блоков. Блок – это виртуальный аналог физического элемента реальной системы. Термин «аналог» предполагает, что блок функционирует, он подчиняется тем же самым уравнениям, что и реальный, моделируемый элемент системы. Виртуальные блоки VisSim могут иметь или вход, на который может быть подан выходной сигнал другого блока, или выход, виртуальный сигнал с которого может быть подан на вход другого блока. Наконец, блоки могут иметь и вход, и выход одновременно. Взаимодействие между блоками отображается т.н. линиями связи, указывающими направление передачи воздействий (сигналов) от одного блока к другому. Взаимодействие между блоками моделируется сигналами - функциями времени, передаваемыми между блоками по линиям связи. Сигналы в модели могут быть измерены с помощью виртуальных измерительных устройств или рассмотрены и изучены с помощью виртуального осциллографа. Внешне виртуальные блоки VisSim с некоторой степенью условности воспринимаются исследователем так же, как реальные устройства. Например, генераторы вырабатывают сигналы, блоки-преобразователи реагируют на входные сигналы в определенном смысле точно так же, как реальные устройства на реальные воздействия, индикаторы показывают величины сигналов. Т.о., принцип построения модели в VisSim состоит в вынесении на рабочее пространство моделей реальных элементов (блоков) и соединении их в соответствии с заранее составленной структурно-алгоритмической схемой моделируемой системы. Такое построение модели из виртуальных блоков очень похоже, с известной степенью условности, на построение реальной системы из настоящих блоков (генераторов, осциллографов, и других устройств) в производственных условиях или на лабораторном стенде.
Основные блоки VisSim
Блоки VisSim можно условно разделить на три основных категории и одну дополнительную: – Блоки, имеющие только выход: генераторы. – Блоки, имеющие вход и выход: преобразователи. – Блоки, имеющие только вход: индикаторы. – Блоки без входов и выходов: надписи, комментарии и др. Важным компонентом модели является соединительная линия - виртуальный аналог физического соединения элементов, передающего сигналы от одного элемента к другому. Соединительные линии в VisSim однонаправленные, передают сигналы с выхода одного блока к входу другого. Генераторы
Генераторы это блоки, имеющие только выход. Генераторы вырабатывают изменяющиеся во времени или постоянные сигналы. Примерами таких блоков в VisSim являются блоки: step (ступенька) - генератор ступенчатой функции ramp (спуск, подъем)- генератор линейно растущего сигнала sinusoid - генератор синусоидального сигнала const - генератор постоянного сигнала, величина которого не меняется в процессе работы модели; slider (скользящий контакт, ползунок) - генератор постоянного сигнала, величину которого можно менять в процессе работы модели.
Рисунок 1.2. – Важные блоки-генераторы программы VisSim.
Для помещения блока на рабочее пространство следует щелкнуть по пункту меню Blocks, перейти на пункт Signal Producer, затем щелкнуть по названию требуемого генератора, перевести курсор в нужное место рабочего пространства и щелкнуть левой кнопкой мыши.
Преобразователи
Преобразователи – это блоки, имеющие входы и выходы. Блоки-преобразователи способны воспринимать воздействия от других блоков, преобразовывать их в соответствии с определенными уравнениями или правилами и выдавать преобразованный сигнал (отклик, реакцию блока) на выход. Важнейшие блоки для моделирования линейных систем: блок transferFunction – передаточная функция. Этот блок позволяет создавать модели как простых, так и очень сложных элементов линейных систем и систем в целом; integrator – блок интегратора, осуществляющий интегрирование входного сигнала по времени; summingJunction – сумматор двух и более сигналов, его выходной сигнал равен алгебраической сумме входных. gain – усилитель.
Рисунок 1.3 – Меню для вызова блока передаточная функция (transferFunction).
Сумматор и усилитель вызываются путем выбора: Blocks → Arithmetic → summingJunction (сумматор) или gain (усилитель). Блок transferFunction является важнейшим при моделировании САУ. Рассмотрим задание параметров данного блока. После размещения на диаграмме блок transferFunction выглядит следующим образом:
Рисунок 1.4 – Вид блока transferFunction до задания параметров
Открытие окна свойств данного блока осуществляется двойным нажатием левой клавиши мыши:
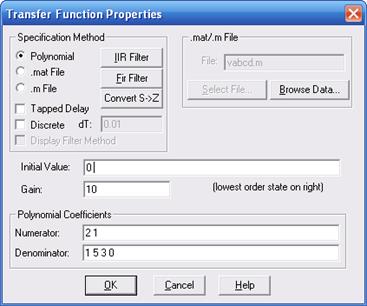
Рисунок 1.5 – Свойства блока transferFunction Задание свойств блока передаточной функции осуществляется следующим образом. Допустим, задана передаточная функция в виде:
Для задания ее в VisSim необходимо соблюдать следующие правила: 1. В поле Gain (коэффициент усиления системы) вводится значение коэффициента усиления 2. В поле Numerator вводятся через пробел коэффициенты полинома числителя передаточной функции в направлении убывания степени p. В нашем случае в данное поле вводятся коэффициенты 3. В поле Denominator вводятся через пробел коэффициенты полинома знаменателя передаточной функции в направлении убывания степени p. В нашем случае в данное поле вводятся коэффициенты 4. Поле Initial Value заполняется в случае, если заданы ненулевые начальные условия. В нашем случае начальные условия не заданы, поэтому оставляем значение по умолчанию равное 0. Примечание: В VisSim с помощью блока transferFunction можно промоделировать только передаточные функции, представляющие правильную дробь, т.е. дробь, в которой степень полинома числителя меньше или равна степени полинома знаменателя (
Примеры: Пример 1. Задана передаточная функция:
Запишем коэффициенты передаточной функции: - коэффициент усиления - полином числителя первого порядка, т.е. вида: - полином знаменателя третьего порядка, т.е. вида:
окно задания свойств выглядит следующим образом:
Вид блока transferFunction после задания свойств:
Пример 2. Задана передаточная функция:
Окно задания свойств:
Вид блока transferFunction после задания свойств:
Блок summingJunction предназначен для задания в модели элемента «сумматор», выполняющего функции суммирования или вычитания сигналов на его входах. После размещения на диаграмме блок имеет вид:
При моделировании САУ зачастую необходимо изменить знак на одном или нескольких входах сумматора и добавить или удалить количество входов. Замена знака на сумматоре производится следующим образом. Наводится курсор мыши на вход сумматора, знак которого нужно изменить, удерживается клавиша Ctrl и производится щелчок левой клавишей мыши по соответствующему входу. Пример сумматора со вторым инвертирующим входом:
Если необходимо добавить или удалить входы, следует нажать на соответствующие кнопки на панели инструментов:
Пример сумматора с четырьмя входами:
Блок Gain имеет один параметр – коэффициент усиления:
Индикаторы
Индикаторы – это блоки, имеющие только вход. Индикаторы программы VisSim предназначены для отображения сигналов в форме удобной и привычной для исследователя. Важнейшими индикаторами являются блоки: – осциллограф - plot; – цифровой индикатор - display. Блоки индикации вызываются путем выбора пунктов меню Blocks → Signal Consumer → plot (display) Виртуальный осциллограф (plot) VisSim представляет собой окно, похожее на экран осциллографа, в котором изображается зависимость наблюдаемых сигналов от времени (рисунок 1.6). На боковой стороне осциллографа помещены условные изображения входов, к которым могут быть подключены выходы других блоков диаграммы для наблюдения поведения их сигналов в зависимости от времени. В VisSim 3.0 на одном блоке plot можно наблюдать от 1 до 4 сигналов, изменяющихся во времени.
Рисунок 1.6 – Виртуальный осциллограф (plot)
Цифровой индикатор display VisSim показывает в цифровом виде значение сигнала на выходе того блока, к которому он подключен. Этот прибор используется для измерения постоянных величин. Надписи и комментарии
Надписи – это блоки без входов и выходов. Эти блоки позволяют создавать на рабочем пространстве диаграммы VisSim текстовые области, которые помогают понять смысл диаграммы. Основной блок: label - надпись. Задание 1 Смоделировать следующие виды сигналов в VisSim: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10)
Значения коэффициентов по вариантам (вариант=№ компьютера).
Таблица 1 – Значения коэффициентов
Промоделировать данные сигналы при шаге моделирования (меню Simulate-SimulationProperties-Step) 1; 0,1, 0,01, 0,001 c.
Задание 2 Задать с помощью блока TransferFunction передаточные функции следующих видов: 1) 2) 3) 4) 5) 6) 7) 8)
Задание 3
Записать передаточную функцию RC-цепочки согласно своему варианту (рисунок 1.9).
Содержание отчета
1. Схемы исследования и результаты моделирования (задание 1). 2. Передаточные функции RC-цепочек, вывод формул (задание 3).
Контрольные вопросы
1. Что такое динамический объект, математическая модель объекта, передаточная функция? 2. Как задать передаточную функцию элемента системы в VisSim? 3. Как изменить шаг моделирования в VisSim?
Рисунок 1.9 – Схемы RC-цепочек Лабораторная работа № 2 Исследование переходных процессов типовых динамических звеньев первого порядка (интегрируещего и апериодического первого порядка)
Цель работы: исследовать переходные процессы идеально-интегрирующего и апериодического первого порядка звеньев.
Общие положения
Анализ САУ удобно вести по эквивалентным структурным схемам, которые представляют собой соединение типовых динамических звеньев, имеющих определенную передаточную функцию. Передаточная функция представляет собой отношение изображений Лапласа выходного и входного сигналов элемента (системы) при нулевых начальных условиях. Зная правила преобразования структурных схем, определяют эквивалентную передаточную функцию системы и уравнение динамики системы. При исследовании динамических звеньев и системы используют регулярные сигналы:
Как системы, так и звенья могут быть устойчивыми (статическими), нейтральными (астатическими) и неустойчивыми. Под устойчивостью понимают способность САУ или звена возвращаться в исходное состояние равновесия после приложения и снятия воздействия. Под типовым динамическим звеном в ТАУ понимается часть САУ, описываемая в динамике алгебраическим или дифференциальным уравнением не выше 2-го порядка. Вид уравнения и определяет название звена. При подаче на вход типового звена регулярных сигналов можно определить его реакцию на данный вид сигнала. Реакция на единичный ступенчатый сигнал 1(t) называется переходной характеристикой h(t); реакция на δ(t) – функция веса или импульсная переходная характеристика ω(t). ω(t)=h'(t), т.к. δ(t)=1(t)'. h(t) и ω(t) являются временными характеристиками звена. При подаче на вход звена гармонического сигнала Частотные свойства звена определяются комплексным коэффициентом передачи:
который представляет собой отношение комплексных амплитуд сигналов на выходе и на входе при подаче на вход гармонического сигнала. При изменении частоты входного сигнала от 0 до ∞ можно исследовать спектр входного и выходного сигналов, т.е. получить АФЧХ – амплитудно-фазовую частотную характеристику – траекторию движения конца вектора комплексного коэффициента передачи W(jω), при изменении частоты от 0 до ∞. АФЧХ отражает соотношение амплитуд и фаз сигналов на выходе и входе. При нулевых начальных условиях уравнение звена в изображениях записывается в виде:
где Y(p), X(p) – изображение по Лапласу выходной и входной величин;
Запишем передаточную функцию, соответствующую уравнению (2):
где
Обычно принято все члены уравнения динамики (2) делить на свободный член – коэффициент
где
Линейные динамические звенья принято классифицировать по виду уравнения динамики: на простейшие (безинерционное, идеально-дифференцирующее, идеально-интегрирующее), звенья 1-го и звенья 2-го порядка. Реакция звена на входной сигнал произвольной формы может быть определена по известной передаточной функции его через обратное преобразование Лапласа:
или решая дифференциальное уравнение при известных начальных условиях и входном сигнале. Если входной сигнал 1(t), т.е.
то определяется переходная функция типовых звеньев h(t):
где Она находится по таблицам, либо по теореме разложения Хэвисайда:
где n – число корней (степень полинома
Изображение по Лапласу гармонических сигналов:
Таким образом, через обратное преобразование Лапласа может быть определена реакция на любой входной сигнал. Звенья 1-го и 2-го порядков можно сформировать на основе блока «интегратор» (идеально-интегрирующего звена), вводя обратные связи. Поэтому при исследовании переходных процессов типовых звеньев необходимо хорошо представлять реакцию идеально-интегрирующего звена на различные типы воздействий. Уравнение динамики интегрирующего звена выглядит следующим образом:
Передаточная функция интегрирующего звена и комплексный коэффициент передачи записываются:
В соответствии с уравнением (5) переходная характеристика – прямая линия с угловым коэффициентом, зависящим от
Скорость изменения выходной величины такого звена пропорциональна входной величине.
Рисунок 2.1 – Переходная характеристика идеально интегрирующего звена
Передаточная функция апериодического звена:
Уравнение переходной характеристики:
Рисунок 2.2 – Переходная характеристика апериодического звена 1-го порядка Порядок выполнения лабораторной работы
Лабораторная работа № 3 Лабораторная работа № 4 Лабораторная работа № 5 Лабораторная работа № 6 Корректирующие средства. Под улучшением качества процесса управления, помимо повышения точности в типовых режимах, понимается изменение динамических свойств системы с целью получения необходимого запаса устойчивости и быстродействия. В этой проблеме основное значение имеет обеспечение запаса устойчивости, т.к. стремление снизить ошибки системы приводит, как правило, к необходимости использовать такие значения коэффициента усиления, при которых без принятия специальных мер система оказывается неустойчивой. При решении задач повышения запасов устойчивости необходимо попытаться рациональным образом изменить ее параметры (коэффициенты передачи отдельных звеньев, постоянные времени и т.п.) так, чтобы удовлетворить требованиям качества. Если это невозможно в систему вводят корректирующие устройства (их иногда называют демпфирующими или стабилизирующими звеньями). Использование того или иного типа КУ определяется удобством технической реализации. КУ последовательного типа особенно удобны в тех случаях, когда в системе используются электрический сигнал в виде напряжения постоянного тока, величина которого линейно связана с сигналом ошибки КУ параллельного типа удобно применять в тех случаях, когда необходимо осуществить сложный закон управления с введение интегралов и производных от сигнала ошибки. КУ обратной связи находят более широкое применение вследствие простоты технической реализации. Это объясняется тем, что на вход КУ обратной связи поступает сигнал довольно высокого уровня, часто непосредственно с выхода системы, с входа усилителя мощности или с выхода исполнительного устройства. Отрицательные обратные связи имеют свойства уменьшать влияние нелинейностей тех участков цепи управления, которые ими охватываются. Так как практически все системы управления содержат те или иные нелинейности (люфт, зона нечувствительности и т.п.), ухудшающие качество работы системы, то использование КУ в виде отрицательных местных обратных связей, как правило, дает возможность добиться лучших результатов по сравнению с другими типами КУ. Можно перейти от КУ одного типа к КУ другого типа, формулы перехода получают приравниванием результирующих передаточных функций (передаточных функций скорректированной системы При последовательном КУ передаточная функция При параллельной коррекции:
При КУ обратной связи
Рисунок 6.1 – Коррекция обратной связью
где
Приравнивая все эти выражения можно получить шесть формул перехода от КУ одного типа к КУ другого типа, например:
Последовательные КУ. Наиболее просто последовательные КУ реализуются на пассивных RC, RL четырехполюсниках и имеют широкое распространение. Они могут быть представлены в виде обобщенной схемы:
 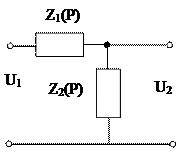
где
Параллельные корректирующие звенья. Параллельные КУ удобно применять при использовании сложных законов управления, когда необходимо вводить производные и интегралы от сигнала ошибки. Введение интеграла позволяет сделать систему астатической и следовательно снизить ошибки, лучше формировать изодромные звенья. Введение производных преследует обычно цель обеспечения устойчивости и запасов устойчивости. Введение интеграла
Рисунок 6.2 – Параллельная коррекция введением интеграла
где
Введение производных
Рисунок 6.3 – Параллельная коррекция введением производных
Обратные связи. Местные ОС могут быть положительными и отрицательными, жесткими и гибкими. Гибкие обратные связи изменяют динамику и работают в переходных режимах, а в установившемся состоянии она как бы отключаются. Жесткая ОС действует как в переходном так и установившемся состоянии. ОС является гибкой, если Введение жестких отрицательных ОС приводит к уменьшению коэффициента передачи и постоянных времени.
Рисунок 6.4 – Коррекция жесткой ОС
Отрицательные корректирующие ОС часто используют для охвата исполнительных двигателей и серводвигателей (вспомогательных двигателей), исполнительных механизмов. Это позволяет снизить влияние нелинейностей и нечувствительности на работу системы. Положительные корректирующие ОС находят значительно меньшее применение. Их можно использовать в качестве так называемых корректоров ошибки. Например:
Рисунок 6.5 – Коррекция положительной ОС
получается изодромное звено с
Методы повышения запаса устойчивости. Повышение запаса устойчивости, или демпфирование, системы сводится, в конечном счете, к рациональному перераспределению полюсов и нулей передаточной функции системы в разомкнутом состоянии. Наиболее наглядно это можно показать на АФЧХ разомкнутой системы, которую нужно с помощью КУ деформировать так, чтобы получить заданные запасы устойчивости. Наиболее просто использовать показатель колебательности М, тогда АФЧХ не должна заходить в окружность соответствующую заданному М.
Рисунок 6.5 – Коррекция положительной ОС
Деформация АФЧХ может быть произведена тремя основны
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 961; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.117.128 (0.011 с.) |

 ;
; ;
; ;
;



 .
. .
.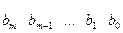 .
. .
.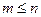 ). При попытке задать передаточную функцию, где
). При попытке задать передаточную функцию, где 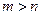 , программа выдаст ошибку.
, программа выдаст ошибку. .
. ;
; , где
, где  ;
;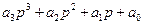 , где
, где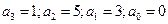 .
.

 .
.






















 , град
, град









 – единичное ступенчатое воздействие;
– единичное ступенчатое воздействие; – единичный импульс;
– единичный импульс; – линейно нарастающий сигнал;
– линейно нарастающий сигнал; – сигнал с постоянным ускорением;
– сигнал с постоянным ускорением; – синусоидальный сигнал.
– синусоидальный сигнал. или
или 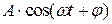 , на его выходе после завершения переходного процесса также наблюдаются колебания.
, на его выходе после завершения переходного процесса также наблюдаются колебания. , (1)
, (1) , (2)
, (2) – комплексная переменная (оператор Лапласа).
– комплексная переменная (оператор Лапласа). , (3)
, (3)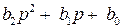 – входной полином;
– входной полином; – выходной полином.
– выходной полином. , тогда уравнение записывают таким образом:
, тогда уравнение записывают таким образом: , (4)
, (4) – коэффициент усиления, размерность которого зависит от Y и X;
– коэффициент усиления, размерность которого зависит от Y и X; ,
,  ,
,  ,
,  – постоянные коэффициенты, обычно имеющие размерность времени;
– постоянные коэффициенты, обычно имеющие размерность времени; ,
,  ,
,  ,
,  .
.

 .
.
 ,
,  – полиномы входной и выходной.
– полиномы входной и выходной. , (5)
, (5) – k-тый корень полинома знаменателя
– k-тый корень полинома знаменателя  .
. ;
; .
. или
или  ,
,  .
. и
и  ,
,  .
. (рисунок 2.1).
(рисунок 2.1). ,
,  ,
,  .
.
 .
. .
.
 . Тогда КУ можно реализовать при помощи R, C, L – элементов.
. Тогда КУ можно реализовать при помощи R, C, L – элементов.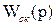 ).
).
 , где
, где  – передаточная функция исходной системы.
– передаточная функция исходной системы. , где
, где  – передаточная функция участка системы к которому подключено КУ.
– передаточная функция участка системы к которому подключено КУ. – передаточная функция участка системы от сумматора до выхода системы.
– передаточная функция участка системы от сумматора до выхода системы.
 ,
, – передаточная функция участка цепи не охваченного ОС.
– передаточная функция участка цепи не охваченного ОС. – передаточная функция элементов охваченных местной ОС.
– передаточная функция элементов охваченных местной ОС.
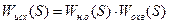

 → последовательное КУ через КУ обратной связи.
→ последовательное КУ через КУ обратной связи. → КУ обратной связи через КУ последовательного типа.
→ КУ обратной связи через КУ последовательного типа.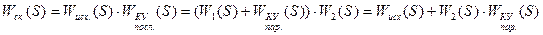


 – сопротивления участков цепи, записанные в операторной форме.
– сопротивления участков цепи, записанные в операторной форме.
 – изодромное звено,
– изодромное звено, – время изодрома.
– время изодрома.

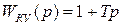 - форсирующее звено.
- форсирующее звено. .
. .
.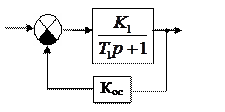


 , при
, при 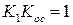
 , т.е. вводится интегрирование на базе апериодического звена.
, т.е. вводится интегрирование на базе апериодического звена.



