
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о математической модели и передаточной функции системыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Динамический объект – это физическое тело, техническое устройство или процесс, имеющее входы – точки возможного приложения внешних воздействий, и воспринимающие эти воздействия, и выходы – точки, значения физических величин в которых характеризуют состояние объекта. Объект способен реагировать на внешние воздействия изменением своего внутреннего состояния и выходных величин, характеризующих его состояние. И воздействие на объект, и его реакция в общем случае изменяются с течением времени, они наблюдаемы, т.е. могут быть измерены соответствующими приборами. Объект имеет внутреннюю структуру, состоящую из взаимодействующих динамических элементов. Воздействием на объект может быть некоторая физическая величина: сила, температура, давление, электрическое напряжение и другие физические величины или совокупность нескольких величин, а реакцией, откликом объекта на воздействие, может быть движение в пространстве, например смещение или скорость, изменение температуры, силы тока и др. Математическая модель – это эквивалент динамического объекта, отражающий в математической форме важнейшие его свойства – законы, которым он подчиняется, связи, присущие составляющим его частям, и т. д. Одним из способов задания математической модели объекта является составление дифференциальных уравнений, описывающих в динамике процесс преобразования входных величин объекта в выходные. При составлении дифференциального уравнения каждого элемента необходимо, прежде всего, выявить физический закон, определяющий его поведение. Математическое выражение соответствующего физического закона и является исходным дифференциальным уравнением данного элемента автоматической системы. Математическим аппаратом, позволяющим представлять дифференциальные уравнения в виде степенных алгебраических уравнений, является преобразование Лапласа. Преобразование Лапласа позволяет ввести некоторую обобщенную модель объекта или системы в виде передаточной функции Передаточная функция представляет собой отношение изображений по Лапласу выходного сигнала элемента САУ или объекта к изображению по Лапласу входного сигнала при нулевых начальных условиях.
Пример. Записать передаточную функцию для RC-цепочки (входная величина – напряжение на входе
Рисунок 1.8 – Схема RC-цепочки
1 способ Записываем уравнение по II закону Кирхгофа:
Учитывая уравнения (2-4), уравнение (1) имеет вид:
Переходим к форме Лапласа, заменяя
Передаточная функция цепи представляет собой отношение
2 способ По закону Ома:
Передаточная функция цепи:
Запишем входное и выходное сопротивления цепи в комплексной форме:
Для перехода к форме Лапласа заменяем
Записываем передаточную функцию цепи:
Порядок выполнения лабораторной работы
Задание 1 Смоделировать следующие виды сигналов в VisSim: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10)
Значения коэффициентов по вариантам (вариант=№ компьютера).
Таблица 1 – Значения коэффициентов
Промоделировать данные сигналы при шаге моделирования (меню Simulate-SimulationProperties-Step) 1; 0,1, 0,01, 0,001 c.
Задание 2 Задать с помощью блока TransferFunction передаточные функции следующих видов: 1) 2) 3) 4) 5) 6) 7) 8)
Задание 3
Записать передаточную функцию RC-цепочки согласно своему варианту (рисунок 1.9).
Содержание отчета
1. Схемы исследования и результаты моделирования (задание 1). 2. Передаточные функции RC-цепочек, вывод формул (задание 3).
Контрольные вопросы
1. Что такое динамический объект, математическая модель объекта, передаточная функция? 2. Как задать передаточную функцию элемента системы в VisSim? 3. Как изменить шаг моделирования в VisSim?
Рисунок 1.9 – Схемы RC-цепочек Лабораторная работа № 2 Исследование переходных процессов типовых динамических звеньев первого порядка (интегрируещего и апериодического первого порядка)
Цель работы: исследовать переходные процессы идеально-интегрирующего и апериодического первого порядка звеньев.
Общие положения
Анализ САУ удобно вести по эквивалентным структурным схемам, которые представляют собой соединение типовых динамических звеньев, имеющих определенную передаточную функцию. Передаточная функция представляет собой отношение изображений Лапласа выходного и входного сигналов элемента (системы) при нулевых начальных условиях. Зная правила преобразования структурных схем, определяют эквивалентную передаточную функцию системы и уравнение динамики системы. При исследовании динамических звеньев и системы используют регулярные сигналы:
Как системы, так и звенья могут быть устойчивыми (статическими), нейтральными (астатическими) и неустойчивыми. Под устойчивостью понимают способность САУ или звена возвращаться в исходное состояние равновесия после приложения и снятия воздействия. Под типовым динамическим звеном в ТАУ понимается часть САУ, описываемая в динамике алгебраическим или дифференциальным уравнением не выше 2-го порядка. Вид уравнения и определяет название звена. При подаче на вход типового звена регулярных сигналов можно определить его реакцию на данный вид сигнала. Реакция на единичный ступенчатый сигнал 1(t) называется переходной характеристикой h(t); реакция на δ(t) – функция веса или импульсная переходная характеристика ω(t). ω(t)=h'(t), т.к. δ(t)=1(t)'. h(t) и ω(t) являются временными характеристиками звена. При подаче на вход звена гармонического сигнала Частотные свойства звена определяются комплексным коэффициентом передачи:
который представляет собой отношение комплексных амплитуд сигналов на выходе и на входе при подаче на вход гармонического сигнала. При изменении частоты входного сигнала от 0 до ∞ можно исследовать спектр входного и выходного сигналов, т.е. получить АФЧХ – амплитудно-фазовую частотную характеристику – траекторию движения конца вектора комплексного коэффициента передачи W(jω), при изменении частоты от 0 до ∞. АФЧХ отражает соотношение амплитуд и фаз сигналов на выходе и входе. При нулевых начальных условиях уравнение звена в изображениях записывается в виде:
где Y(p), X(p) – изображение по Лапласу выходной и входной величин;
Запишем передаточную функцию, соответствующую уравнению (2):
где
Обычно принято все члены уравнения динамики (2) делить на свободный член – коэффициент
где
Линейные динамические звенья принято классифицировать по виду уравнения динамики: на простейшие (безинерционное, идеально-дифференцирующее, идеально-интегрирующее), звенья 1-го и звенья 2-го порядка. Реакция звена на входной сигнал произвольной формы может быть определена по известной передаточной функции его через обратное преобразование Лапласа:
или решая дифференциальное уравнение при известных начальных условиях и входном сигнале. Если входной сигнал 1(t), т.е.
то определяется переходная функция типовых звеньев h(t):
где Она находится по таблицам, либо по теореме разложения Хэвисайда:
где n – число корней (степень полинома
Изображение по Лапласу гармонических сигналов:
Таким образом, через обратное преобразование Лапласа может быть определена реакция на любой входной сигнал. Звенья 1-го и 2-го порядков можно сформировать на основе блока «интегратор» (идеально-интегрирующего звена), вводя обратные связи. Поэтому при исследовании переходных процессов типовых звеньев необходимо хорошо представлять реакцию идеально-интегрирующего звена на различные типы воздействий. Уравнение динамики интегрирующего звена выглядит следующим образом:
Передаточная функция интегрирующего звена и комплексный коэффициент передачи записываются:
В соответствии с уравнением (5) переходная характеристика – прямая линия с угловым коэффициентом, зависящим от
Скорость изменения выходной величины такого звена пропорциональна входной величине.
Рисунок 2.1 – Переходная характеристика идеально интегрирующего звена
Передаточная функция апериодического звена:
Уравнение переходной характеристики:
Рисунок 2.2 – Переходная характеристика апериодического звена 1-го порядка Порядок выполнения лабораторной работы
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 2270; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 .
.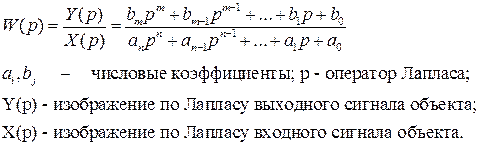
 , выходная величина – выходное напряжение
, выходная величина – выходное напряжение  ) (рисунок 1.8).
) (рисунок 1.8).
 . (1)
. (1) ; (2)
; (2) ; (3)
; (3) . (4)
. (4) – дифференциальное уравнение (ДУ) цепи.
– дифференциальное уравнение (ДУ) цепи. . ДУ примет вид:
. ДУ примет вид: . (5)
. (5) . Из уравнения (5):
. Из уравнения (5): , где
, где  – постоянная времени цепи.
– постоянная времени цепи.
 .
. .
. ;
; .
. :
: ;
; .
. .
.













 , град
, град









 – единичное ступенчатое воздействие;
– единичное ступенчатое воздействие; – единичный импульс;
– единичный импульс; – линейно нарастающий сигнал;
– линейно нарастающий сигнал; – сигнал с постоянным ускорением;
– сигнал с постоянным ускорением; – синусоидальный сигнал.
– синусоидальный сигнал. или
или 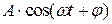 , на его выходе после завершения переходного процесса также наблюдаются колебания.
, на его выходе после завершения переходного процесса также наблюдаются колебания. , (1)
, (1) , (2)
, (2) – комплексная переменная (оператор Лапласа).
– комплексная переменная (оператор Лапласа). , (3)
, (3)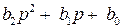 – входной полином;
– входной полином; – выходной полином.
– выходной полином. , тогда уравнение записывают таким образом:
, тогда уравнение записывают таким образом: , (4)
, (4) – коэффициент усиления, размерность которого зависит от Y и X;
– коэффициент усиления, размерность которого зависит от Y и X; ,
,  ,
,  ,
,  – постоянные коэффициенты, обычно имеющие размерность времени;
– постоянные коэффициенты, обычно имеющие размерность времени; ,
,  ,
,  ,
,  .
.

 .
.
 ,
,  – полиномы входной и выходной.
– полиномы входной и выходной. , (5)
, (5) – k-тый корень полинома знаменателя
– k-тый корень полинома знаменателя  .
. ;
; .
. или
или  ,
,  .
. и
и  ,
,  .
. (рисунок 2.1).
(рисунок 2.1). ,
,  ,
,  .
.
 .
. .
.



