
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача решена, осталось только вывести результаты.Содержание книги
Поиск на нашем сайте
Этап 7. Вывод ответа
Соберем все воедино в функции otvet:
1) Выполним проверку на линейную зависимость. 2) Выполним прямой ход, если значение matr удовлетворяет условию. 3) Затем обратный ход с аналогичной проверкой. 4) И присвоим matr полученный результат. 5) Вернем значение функции (им может быть или матрица-столбец с корнями системы или одно из двух сообщений) В заключении выведем ответ, набрав otvet =. Ответ может быть трех типов:
Пример программы в MathCAD
Контрольные вопросы
1. Какой вид имеет матрица коэффициентов после окончания прямого хода в методе Гаусса? 2. Какие операции выполняются при обратном ходе? 3. Какие преимущества имеет модифицированный метод Гаусса по сравнению с обычным методом?
Лабораторная работа 3 Решение систем линейных алгебраических уравнений методом итераций Работа выполняется с использованием палитры программирования системы автоматизации математических вычислений Mathcad
Задание на работу: 1. Разработать программу для решения системы линейных алгебраических уравнений методом итераций. 2. В программе предусмотреть проверку существования единственного решения, воспользовавшись процедурой «proverka», рассмотренной в работе № 2. 3. В программе предусмотреть вывод числа итераций, необходимых для достижения заданной точности (точность определяется погрешностью ε) 4. Решить систему уравнений, определенную вариантом задания (задания определены в работе № 2, погрешность ε положить равной 0.0001). 5. Найти теоретическую оценку числа итераций, необходимых для достижения заданной точности, и сравнить с фактическим значением. 6. Произвести проверку решения с помощью процедуры решения системы линейных алгебраических уравнений isolve (X:= isolve(A,В)). 7. Изменить матрицу коэффициентов А, сделав систему уравнений линейно зависимой, и проверить работоспособность программы в этом случае.
Требования к оформлению отчета Отчет должен содержать: - Название и цель работы - Задание на работу - Текст программы на Mathcadе - Результаты работы программы - Проверку решения
Контрольные вопросы
1. В каком случае целесообразно применять итерационный метод решения систем линейных алгебраических уравнений? 2. Сформулируйте условие сходимости итерационного процесса. 3. Что такое l – норма матрицы? 4. Что такое m – норма матрицы? 5. Как оценить количество итераций, необходимое для достижения заданной точности?
Примечание: при выполнении работы используйте вспомогательные материалы, приведенные в работе № 2.
Раздел 3 Решение нелинейных уравнений Краткое введение. Пусть f(x) = 0 - некоторое уравнение. Число ξ называется корнем или решением данного уравнения, если оно, будучи подставлено в уравнение, обращает его в равенство, т. е. f (ξ) = 0. Число ξ называют также нулем функции y = f(x). Нахождение действительных корней с определенной точностью можно разбить на два этапа: 1. отделение корней, т. е. установление промежутков, в которых содержится один корень уравнения; 2. вычисление корня, принадлежащего выбранному промежутку, с заданной точностью. Для отделения корней составляют таблицу значений функции y = f(x) на определенном промежутке изменения аргумента х, и если окажется, что для соседних значений аргументов значения функции имеют разные знаки, то нуль находится между ними. Возможны и другие способы отделения корней, например графические. После отделения корней для вычисления корня можно применить следующие методы. Метод половинного деления Описание метода. Пусть дано уравнение f(x) = 0, (1) причем функция f(x) непрерывна на отрезке [ a, b] и f(a)f(b) < 0. Для вычисления корня уравнения (1), принадлежащего отрезку [ a, b], найдем середину этого отрезка x1 = (a + b) / 2. Если f(x1) Новый суженный промежуток [ a1, b1 ] снова делим пополам и продолжаем вычисления по разработанной схеме и т. д. В результате получаем либо точный корень уравнения (1) на каком - то этапе, либо последовательность вложенных отрезков [ a, b ], [ a1, b1 ], ..., [ a n, b n ],.. таких, что f(a n)f(b n) < 0 (n = 1, 2,...), (2) b n - a n = (1/ 2 n) (b- a) (3) Число ξ - общий предел последовательности { a n } и { b n } - является корнем уравнения
f(x) = 0. Оценку погрешности решения на n -ом шаге вычислений можно получить из соотношения (3) в виде
0 < ξ - a n Здесь a n
 
       
Рис. 3.1 Наличие единственного корня уравнения на интервале [a,b]
Блок – схема алгоритма, реализующего метод половинного деления, приведена на рис. 3.3.
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 317; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.81.181 (0.009 с.) |

 Создадим матрицу-столбец a из последнего столбца матрицы matr и возвратим ее.
Создадим матрицу-столбец a из последнего столбца матрицы matr и возвратим ее.





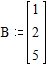










 0, то для продолжения вычислений выберем ту из частей банного отрезка [ a, x1] или [ x1, b], на концах которой функция f(x) имеет противоположные знаки. Концы нового отрезка обозначим через a1 и b1 .
0, то для продолжения вычислений выберем ту из частей банного отрезка [ a, x1] или [ x1, b], на концах которой функция f(x) имеет противоположные знаки. Концы нового отрезка обозначим через a1 и b1 . (1/ 2 n) (b- a) = b n - a n (4)
(1/ 2 n) (b- a) = b n - a n (4) ξ c точностью ε не превышающей (1/ 2 n) (b- a).
ξ c точностью ε не превышающей (1/ 2 n) (b- a).








