
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Итерационный метод решения нелинейных уравненийСодержание книги
Поиск на нашем сайте
Пусть требуется решить уравнение, представленное в виде x = g (x), (5) где правая часть уравнения - непрерывная на отрезке функция g (x). Суть метода итераций (метода последовательных приближений)состоит в следующем. Начиная с произвольной точки x0, принадлежащей отрезку [a, b], последовательно получаем x (1) = g (x (0)) (первое приближение) x (2) = g (x (1)) (второе приближение) … … … x (k + 1) = g (x (k)) (k + 1-е приближение) Последовательность x (0), x (1), …, x (k), … (6) называется последовательностью итераций для уравнения (1) с начальной точкой x (0). Если все точки (2) принадлежат отрезку [a, b] и существует предел
x (k + 1) = g (x (k)) (k = 0,1,2,...), (7) получим Следовательно, если существует предел последовательности итераций (7), то он является корнем уравнения (1). Достаточные условия сходимости последовательности итераций содержатся в следующей теореме.
Теорема.
1) 2) значения функции y = g(х) принадлежат отрезку [a,b] для любого x Тогда при любом выборе начального приближения x(0) Оценка погрешности k -го приближения x (k) к корню
где Укажем теперь один из способов преобразования уравнения f(x) = 0 (9) к виду x = g(x), допускающему применение метода итераций, сходящихся к решению Для любого числа g (x) = x + Предположим, что производная f ' (x) > 0 и непрерывна на [ a,b ]. Пусть положим
и рассмотрим функцию
Для функции, определенной формулой (10), выполняются достаточные условия сходимости метода итераций решения уравнения (9). В частности, условие 1) теоремы следует из неравенств 0 < m 0 Замечание1. Если окажется, что производная f ' (x) отрицательна на отрезке [ a, b], то уравнение (1) можно заменить на равносильное уравнение -f(x) = 0 и использовать указанное преобразование. Замечание 2. Если вычисление точного числа Замечание 3. При нахождении корня уравнения (1) с заданной точностью или при оценке погрешности k-го приближения можно, не вычисляя точного значения числа q = max | g ' (x) |,ограничиться следующей практической рекомендацией:
Блок – схема алгоритма, реализующего итерационный метод, приведена на рис. 3.2.
                        
       
  
        
  
Рис 3.3 Блок – схема алгоритма, реализующего метод половинного деления
Лабораторная работа 4 Решение нелинейных уравнений Работа выполняется с использованием палитры программирования системы автоматизации математических вычислений Mathcad
Задание на работу: 1.Разработать программы нахождения корней нелинейного уравнения методом половинного деления и методом итераций. 2.Найти корень заданной функции с требуемой точностью (eps = 0.0001). 3. Сравнить количество итераций, требуемых для нахождения решения с заданной точностью тем и другим методом. 4. Задать линейную функцию, имеющую корень на том же самом интервале [a,b] и решить данное линейное уравнение. Сравнить число итераций в том и другом методе. Объяснить полученные результаты.
Варианты заданий. 1. x 4 - 3x -20 = 0 (x > 0) 2. x 3 - 2x - 5 = 0 (x > 0) 3. x 3 + 3x + 5 = 0 4. x 4 + 5x -7 = 0 (x > 0) 5. x 3 - 12x - 5 = 0 (x > 0) 6. x 3 - 2x 2 - 4x + 5 = 0 (x < 0) 7. x + e x = 0 8. x 5 - x - 2 = 0 9. x 3 - 10x + 5 = 0 (x < 0) 10. 2 - lnx - x = 0 11. x 3 + 2x - 7 = 0 12. x 3 + x 2 - 11 = 0 (x > 0) 13..x 4 - 2x - 4 = 0 (x > 0) 14. 2e x + x - 1 = 0 15. x 4 - 2x - 4 = 0 (x < 0) 16. 2x 3 + x 2 - 4 = 0 (x > 0) 17. e x - x - 2 = 0 18. (1/2) e x - x - 1 = 0 (x > 0) 19. x 2 - cos x = 0 (x > 0) 20. x 2 + lnx = 0 Требования к оформлению отчета Отчет по лабораторной работе должен содержать: - название работы - цель работы - тексты программ - результаты, полученные в процессе выполнения работы - выводы Вспомогательные материалы Для разработки программ на Mathcad е можно использовать приемы, описанные в лабораторных работах №1 и №2. Существует бесчисленное множество линейных функций, имеющих корень на интервале[a,b]. Поясним это на примере. Пусть a = 2, b = 7. Пусть корень уравнения равен 5. Тогда функция F(x) = k1 + k2*x, имеющая корень, равный пяти, может иметь такой вид F(x) = 10 – 2*x (один из коэффициентов задается произвольно, другой находится из уравнения F(x) = 0).
Контрольные вопросы: 1. Зачем нужна процедура отделения корней? 2. Что называется корнем уравнения? 3. Какова точность метода половинного деления? 4. Каким образом исходное уравнение преобразуется к виду, удобному для итераций? 5. Чему равна оценка погрешности k -го приближения? Раздел 4 Интерполирование функций Краткое введение. Постановка задачи интерполирования. На отрезке
Требуется построить интерполирующую функцию F(x), принадлежащую известному классу и принимающую в узлах интерполяции те же значения, что и
Рис. 4.1 Интерполирование функции y = f(x)
В общем случае, задача имеет бесчисленное множество решений. Задача становится однозначной, если решение искать в заданном классе функций. Будем искать полином Полученную интерполяционную формулу Если При
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 415; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.255.247 (0.011 с.) |


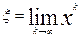 , то, перейдя к пределу в равенстве
, то, перейдя к пределу в равенстве , т.е.
, т.е. 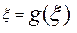 .
. Пусть функция g (x) имеет на отрезке [a, b] непрерывную производную и выполнены два условия:
Пусть функция g (x) имеет на отрезке [a, b] непрерывную производную и выполнены два условия: q < 1 при x
q < 1 при x  [a, b];
[a, b]; уравнения (1) на отрезке [a, b]
уравнения (1) на отрезке [a, b] , (8)
, (8)
 уравнение (9) равносильно уравнению (5), где
уравнение (9) равносильно уравнению (5), где f(x).
f(x).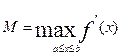 ,
,  ;
;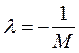 ,
, 
 . (10)
. (10) f ' (x)
f ' (x)  .
. затруднительно, то можно заменить его произвольным числом М1> M. Однако при большом М1 число q = 1 - m / М1 ближе к единице и процесс итераций сходится медленнее.
затруднительно, то можно заменить его произвольным числом М1> M. Однако при большом М1 число q = 1 - m / М1 ближе к единице и процесс итераций сходится медленнее. при 0 < q
при 0 < q  при (1/2) < q < 1. (12)
при (1/2) < q < 1. (12)




 0
0


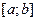 заданы n+1 точки
заданы n+1 точки  , которые называются узлами интерполяции, и значение некоторой функции
, которые называются узлами интерполяции, и значение некоторой функции  в этих точках
в этих точках . (1)
. (1)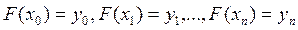 (2)
(2)
 степени не выше n и удовлетворяющий условию (2).
степени не выше n и удовлетворяющий условию (2). используют для вычисления значений
используют для вычисления значений  - имеет место задача интерполирования (интерполирование “в узком смысле”).
- имеет место задача интерполирования (интерполирование “в узком смысле”).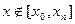 решается задача экстраполирования.
решается задача экстраполирования.


