
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение систем нелинейных уравнений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Метод простых итераций (последовательных приближений). Систему нелинейных уравнений можно записать в векторном виде
или подробно в координатном виде Нулевое приближение в случае двух переменных находится графически: на плоскости Для трех и более переменных удовлетворительных способов подбора нулевых приближений нет. Заменим нелинейную систему (1) эквивалентной системой вида
или Если итерации сходятся, то они сходятся к решению уравнения (предполагается, что решение существует). Исследуем сходимость итераций. Обозначим компоненты решения через
Заканчивать итерации можно по критерию сходимости:
Средства пакета MathCAD для решения нелинейных уравнений
Для решения систем имеется специальный вычислительный блок, состоящий из трех частей, идущих последовательно друг за другом: - Given – ключевое слово; - Система уравнений или неравенств, записанная логическими операторами в виде равенств или неравенств; - Find (x1,...,x n) – встроенная функция для решения системы относительно переменных x1,...,x. Блок Given/Find использует для поиска решения итерационные методы, поэтому, как и для функции root, требуется задать начальные значения для всех x1,...,x n. Начальные условия определяют начальные значения искомых переменных и задаются в виде var:=value, т.е. обычным присваиванием переменным заданных значений, причем задать их необходимо до ключевого слова Given. Уравнения задаются в виде expr_left=expr_right с применением логического знака равенства между левой и правой частями каждого уравнения, который вводится либо с панели инструменов. Boolean (Булевы операторы), сочетанием клавиш<Ctrl>+<=>. Функция Find возвращает вектор значений, составленный из решения по каждой переменной. Таким образом, число элементов вектора равно числу аргументов функции Find. Пример 4. Решить систему уравнений
Ответ: решением системы является точка (-0.106, 1.056). Замечание. Вычислительный блок использует константу CTOL в качестве погрешности выполнения уравнений, введенных после ключевого слова Given. Например, если CTOL =0.001, то уравнение х=10 будет считаться выполненным и при х=10,001, и при х=9,999. Вычислительным блоком с функцией Find можно найти и корень уравнения с одним неизвестным. Действие Find в этом случае совершенно аналогично уже рассмотренным примерам. Задача поиска корня рассматривается как решение системы, состоящей из одного уравнения. Единственным отличием будет скалярный, а не векторный тип числа, возвращаемого функцией Find.
Если окрестность, в которой требуется найти решение системы, не задана, начальное приближение для решения можно задать, построив в одной графической области графики кривых, задаваемых уравнениями системы.
Пример 5. Найти решение системы уравнений
На графике видно, что в качестве начального приближения можно выбрать, например, точку (0,0). Далее используя вычислительный блок и функцию, решение системы.
Ответ: решением системы является точка (-1.118, -0.653).
Иногда приходится заменять задачу отделения корней системы уравнений задачей поиска экстремума функции многих переменных. Например, когда невозможно найти решение с помощью функции Find, можно попытаться потребовать вместо точного выполнения уравнений условий минимизировать их невязку. Для этого следует в вычислительном блоке вместо функции Find использовать функцию Minerr, имеющую тот же самый набор параметров. Она также должна находиться в пределах вычислительного блока: 1. x1:=c1... xn: =сn – начальные значения для неизвестных. 2. Given - ключевое слово. 3. Система алгебраических уравнений и неравенств, записанная логическими операторами. 4. Minerr (x1,...,хn) – приближенное решение системы относительно переменных x1,...,хn, минимизирующее невязку системы уравнений.
Пример 6. Использование функции Minerr
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 607; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 (1)
(1) .
.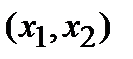 строят кривые
строят кривые  и
и  и находят точки их пересечения.
и находят точки их пересечения. . (2)
. (2)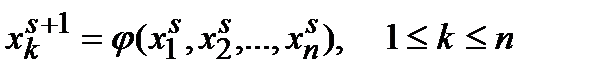 .
. и преобразуем погрешность очередной итерации:
и преобразуем погрешность очередной итерации: где l – направление, соединяющее многомерные точки
где l – направление, соединяющее многомерные точки  и
и 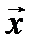 , а
, а  – некоторая точка, лежащая между ними на этом направлении. Это равенство означает, что вектор погрешности нового приближения равен матрице производных, умноженной на вектор погрешности предыдущего приближения. Если какая-нибудь норма матрицы производных
– некоторая точка, лежащая между ними на этом направлении. Это равенство означает, что вектор погрешности нового приближения равен матрице производных, умноженной на вектор погрешности предыдущего приближения. Если какая-нибудь норма матрицы производных  , согласованная с некоторой нормой вектора, меньше единицы, то норма погрешности убывает от итерации к итерации по геометрической прогрессии. Это означает линейную сходимость метода.
, согласованная с некоторой нормой вектора, меньше единицы, то норма погрешности убывает от итерации к итерации по геометрической прогрессии. Это означает линейную сходимость метода. , выполнение которого необходимо проверить для каждой компоненты.
, выполнение которого необходимо проверить для каждой компоненты. в окрестности точки
в окрестности точки  .
.










