
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3: Численные методы решения нелинейных уравнений и оптимизация функций.Содержание книги
Поиск на нашем сайте
Цель работы: Изучить вычислительные возможности пакета MathCAD для решения оптимизационных задач. Используемые программные средства: пакет MathCAD. Теоретические сведения. Решение уравнения с одним неизвестным. Метод простых итераций. Пусть задана непрерывная функция f(x) и требуется найти корни уравнения f Уравнение (1) заменим эквивалентным ему уравнением
Выберем некоторое нулевое приближение и вычислим последующие приближения по формулам:
Процесс итераций сходится
Метод Ньютона. Пусть дано уравнение f(x) = 0,корень которого В методе касательных (n +1)-е приближение вычисляется по формуле Оценка абсолютной погрешности определяется формулой
Средства пакета MathCAD для решения нелинейных уравнений Для решения алгебраических уравнений MathCAD имеет встроенную функцию root, которая, в зависимости от типа задачи, может включать либо два, либо четыре аргумента и, соответственно, работает по-разному. - root (f(х),х); - root(f(х),х,а,b); где f(х) – скалярная функция, определяющая уравнение; х – скалярная переменная, относительно которой решается уравнение; а, b – границы интервала, внутри которого происходит поиск корня. Первый тип функции root требует дополнительного задания начального значения (guess value) переменной х. Для этого нужно предварительно присвоить этой переменной некоторое число, в окрестности которого будет производиться поиск корня. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня. Эту Отделить корень можно, построив график функции f(х) и с помощью опции Trace (см.лабораторную работу № 3)определить примерно абсциссу пересечения графиком оси ОХ.
Пример 1. Рассмотрим уравнение sin(x) = 0, корни которого известны заранее.
Поиск корня алгебраического уравнения в заданном интервале Когда root имеет четыре аргумента, следует помнить о двух ее особенностях:
- внутри интервала [а,b] не должно находиться более одного корня, иначе будет найден один из них, заранее неизвестно какой именно; - значения f(а) и f(b) должны иметь разный знак, иначе будет выдано сообщение об ошибке.
Поиск мнимых корней уравнения. Если уравнение не имеет действительных корней, но имеет мнимые, то их также можно найти.
Замечание. Явный вид функции f(х) может быть определен непосредственно в теле функции root. Корни полинома Если функция f(х) является полиномом, то все его корни можно определить, используя встроенную функцию polyroots(v), где v – вектор, составленный из коэффициентов полинома. Поскольку полином n -й степени имеет ровно n корней (некоторые из них могут быть кратными), вектор v должен состоять из n+1 элемента. Результатом действия функции polyroots является вектор, составленный из n корней рассматриваемого полинома. При этом нет надобности вводить какое-либо начальное приближение, как для функции root.
Пример 3.
Следует обратить внимание, что численный метод вместо двух из трех действительных единичных корней (иными словами, кратного корня 1) выдает два мнимых числа. Однако малая мнимая часть этих корней находится в пределах погрешности, определяемой константой TOL, и не должна вводить пользователей в заблуждение. В данном случае следует помнить, что корни полинома могут быть комплексными, и ошибка вычислений может сказываться как на действительной, так и на комплексной части искомого корня. Символьное решение уравнений. Некоторые уравнения можно решить точно с помощью символьного процессора MathCAD. Делается это очень похоже на численное решение уравнений с применением вычислительного блока. Присваивать неизвестным начальные значения нет необходимости.
Пример 4.
Вместо знака равенства после функции Find в листингах следует знак символьных вычислений, который можно ввести с панели Symbolic (Символика) или, нажав клавиши <Ctrl>+<.>. При этом уравнения должны иметь вид логических выражений (знаки равенства нужно вводить с помощью панели Booleans (Булевы операторы)). С помощью символьного процессора решить уравнение с одним неизвестным можно и другим способом:
1. Введите уравнение, пользуясь панелью Booleans (Булевы операторы) или нажав клавиши <Ctrl>+<.> для получения логического знака равенства. 2. Щелчком мыши выберите переменную, относительно которой требуется решить уравнение. 3. Выберите в меню Symbolics (Символика) пункт Variable/Solve (Переменная/Решить). После строки с уравнением появится строка с решением или сообщение о невозможности символьного решения этого уравнения. Символьные вычисления могут производиться и над уравнениями, которые помимо неизвестных содержат различные параметры.
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 298; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.228.15 (0.009 с.) |

 (1)
(1) (2)
(2) (3)
(3) , если выполнено условие
, если выполнено условие  на отрезке [ a, b ], содержащем корень
на отрезке [ a, b ], содержащем корень  .
. отделен. Суть метода состоит в том, что дуга кривой
отделен. Суть метода состоит в том, что дуга кривой  заменяется касательной к ней и за приближение корня берется абсцисса точки пересечения касательной с осью OX.
заменяется касательной к ней и за приближение корня берется абсцисса точки пересечения касательной с осью OX. ,
,  , в которой за нулевое приближение
, в которой за нулевое приближение  принимается такое значение из отрезка [ a, b ], для которого выполняется условие
принимается такое значение из отрезка [ a, b ], для которого выполняется условие  .
. , где
, где 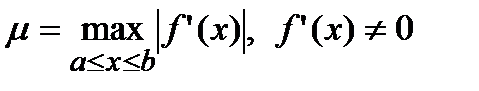 .
.









