
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приближенное решение дифференциальных уравнений.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Метод Эйлера. Пусть требуется решить задачу Коши: найти решение дифференциального уравнения
удовлетворяющее начальному условию у(х0) = у0. При численном решении дифференциального уравнения (1) задача ставится следующим образом: в точках хк, х0, х1, х2,...., хп найти приближения Разность xk = x0 +kh где Метод Эйлера основан на непосредственной замене производной разностным отношением по приближенной формуле
Приближенное значение ук в точке xk = x0 +kh вычисляется по формуле:
Пример 4.1: Методом Эйлера найти значения решения уравнения Решение. По формуле (2) находим точки х0 = 1, х1 = 1,1, х2 = 1,2, х3 = 1,3, х4 = 1,4, х5 = 1,5. Значения искомой функции у = у(х), удовлетворяющей условиям данной задачи Коши, вычисляем по формуле (4). Результаты вычислений занесем в таблицу.
§2. Метод Рунге – Кутта. (Один из наиболее употребляемых методов повышенной точности). Пусть функция у определяется дифференциальным уравнением
Если положить
Получаем следующую схему вычислений:
Пример 4.2: Составь таблицу значений функции у, определяемой уравнением Решение. Используя формулы (5) найдем числа:
Отсюда Таким образом у1 = 1 + 0,1832 = 1,1832 при х = 0,2. По этой же схеме находим у2 и т.д. процесс вычисления ведем по схеме:
Упражнения. 1. Найти, используя метод Эйлера, значения функции у, определяемой дифференциальным уравнением
Ответ:
2. Найти по методу Эйлера четыре значения функции у, определяемой уравнением
Ответ:
3. Найти по методу Эйлера три значения функции у, определяемой уравнением
Ответ:
4. Найти по методу Эйлера четыре значения функции у, определяемой уравнением
Ответ:
5. Найти, используя метод Эйлера, значения функции у, определяемой дифференциальным уравнением
Ответ:
6. Найти методом Эйлера численной решение уравнения
Ответ:
7. По методу Рунге – Кутта проинтегрировать уравнение Ответ:
8. По методу Рунге – Кутта проинтегрировать уравнение Ответ:
9. По методу Рунге – Кутта проинтегрировать уравнение Ответ:
Литература.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 1966; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.91.152 (0.006 с.) |

 (1)
(1) для значений точного решения у(хк)
для значений точного решения у(хк)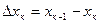 называется шагом сетки. Во многих случаях величину
называется шагом сетки. Во многих случаях величину  принимают постоянной. Пусть
принимают постоянной. Пусть  (2)
(2)  , где
, где  (3)
(3) - формула Эйлера (4)
- формула Эйлера (4) , для которого у(1) = 1, в пяти точках отрезка [ 1; 1,5 ], приняв h = 0,1.
, для которого у(1) = 1, в пяти точках отрезка [ 1; 1,5 ], приняв h = 0,1. с начальным условием у(х0) = у0. При численном интегрировании такого уравнения по методу Рунге – Кутта определяются четыре числа:
с начальным условием у(х0) = у0. При численном интегрировании такого уравнения по методу Рунге – Кутта определяются четыре числа: (5)
(5) , то можно доказать, что
, то можно доказать, что . (6)
. (6)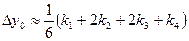











 , при начальном условии у(0) = 1, 0 ≤ х ≤ 1 при h = 0,2.
, при начальном условии у(0) = 1, 0 ≤ х ≤ 1 при h = 0,2.

 , при начальном условии у(0) = 1, принимая h = 0,1. Ограничиваясь отысканием первых четырех значений у.
, при начальном условии у(0) = 1, принимая h = 0,1. Ограничиваясь отысканием первых четырех значений у.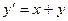 , при начальном условии у(0) = 1, принимая h = 0,1.
, при начальном условии у(0) = 1, принимая h = 0,1. , при начальном условии у(0) = 1, принимая h = 0,1.
, при начальном условии у(0) = 1, принимая h = 0,1. , при начальном условии у(0) = 0, принимая h = 0,1.
, при начальном условии у(0) = 0, принимая h = 0,1. , при начальном условии у(2) = 4, принимая h = 0,1. Ограничиваясь отысканием первых четырех значений у.
, при начальном условии у(2) = 4, принимая h = 0,1. Ограничиваясь отысканием первых четырех значений у. на отрезке [0; 1], при начальном условии у(0) = 1, принимая h = 0,2
на отрезке [0; 1], при начальном условии у(0) = 1, принимая h = 0,2 на промежутке [1; 2], при начальном условии у(1) = 0, принимая h = 0,1. В первых пяти точках.
на промежутке [1; 2], при начальном условии у(1) = 0, принимая h = 0,1. В первых пяти точках. на промежутке [0; 1], при начальном условии у(0) = 1, принимая h = 0,1. Вычисление вести с тремя верными знаками.
на промежутке [0; 1], при начальном условии у(0) = 1, принимая h = 0,1. Вычисление вести с тремя верными знаками. на промежутке [0; 1], при начальном условии у(0) = 1, принимая h = 0,1. Вычисление вести с двумя верными знаками.
на промежутке [0; 1], при начальном условии у(0) = 1, принимая h = 0,1. Вычисление вести с двумя верными знаками.


