
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приближенное вычисление определенных интегралов.Содержание книги Поиск на нашем сайте
Пусть требуется найти определенный интеграл Наиболее употребимые формулы – формула прямоугольников, формула трапеции и формула парабол (Симпсона), основанные на геометрическом смысле определенного интеграла. Метод прямоугольников.
т.е.
Абсолютная погрешность метода определяется неравенством:
где Пример 3.1: Вычислить интеграл Решение.
= т.к.
Следовательно:
Пример 3.2: Зная, что погрешность метода прямоугольников при вычислении интеграла Решение. Используя формулу (2) получим Умножим правую и левую части неравенства на дробь т.е Метод трапеций. Формулу трапеций получают аналогично формуле прямоугольников: на каждом частичном отрезке криволинейная трапеция заменяется обычной.
Так как площадь криволинейной трапеции приблизительно равна сумме площадей трапеций Si, высота каждой из которых равна h, то:
Абсолютная погрешность метода (аналогично методу прямоугольников) составляет:
тогда Пример 3.3: Вычислить интеграл Решение. По формуле трапеций:
Тогда
Найдем погрешность:
Следовательно
§3. Метод парабол (Метод Симпсона). Если заменить график функции на каждом отрезке
Пусть парабола проходит через точки М1 (-h; у0), М2 (0; у1) и М3 (h; у2).
тогда полученная площадь:
(7) Выразим полученное значение через у0, у1 и у2. Используя формулы (6) получим c = y1,
Вывод формулы парабол (Симпсона). Пусть дана криволинейная трапеция, ограниченная функциями y = f (x), x = a, x = b, y = 0.
y = f (x): у0, у1, у2,......, у2п-2, у2п-1, у2п.
На отрезке [ x0; x2 ] парабола проходит через точки (х0; у0), (х1; у1), (х2; у2). Используя формулу (8) получим Аналогично на отрезке [ x2; x4 ]:
Следовательно:
Учитывая погрешность вычислений
Абсолютная погрешность метода оценивается соотношением:
Пример 3.4: Вычислить интеграл Решение. Количество разбиений 2п = 8, Составим таблицу:
Рассмотрим погрешность метода:
По формуле Симпсона получаем:
Точное решение: Упражнения.
(Ответ:
(Ответ:
(Ответ:
(Ответ: п = 10,
(Ответ: п = 5,
(Ответ: п = 4,
(Ответ: п = 4,
(Ответ: п = 6,
ГЛАВА IV.
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 790; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.201.243 (0.008 с.) |

 от непрерывной функции f(x). Если можно найти первообразную F(x) функции f(x), то интеграл вычисляется по формуле Ньютона – Лейбница. Но не всегда первообразная функции выражается через элементарные функции. В этих и других случаях используют приближенные формулы, с помощью которых определенный интеграл находится с любой степенью точности.
от непрерывной функции f(x). Если можно найти первообразную F(x) функции f(x), то интеграл вычисляется по формуле Ньютона – Лейбница. Но не всегда первообразная функции выражается через элементарные функции. В этих и других случаях используют приближенные формулы, с помощью которых определенный интеграл находится с любой степенью точности.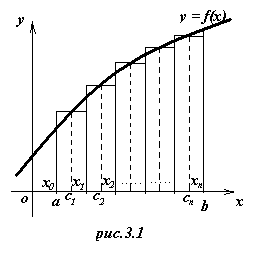 Пусть на отрезке [a; b], где a < b, задана непрерывная функция f(x). Требуется вычислить интеграл
Пусть на отрезке [a; b], где a < b, задана непрерывная функция f(x). Требуется вычислить интеграл  . тогда xi = x0+hi. В середине
. тогда xi = x0+hi. В середине  каждого такого отрезка построим ординату
каждого такого отрезка построим ординату  графика функции у = f(x). Приняв эту ординату за высоту построим прямоугольник с площадью
графика функции у = f(x). Приняв эту ординату за высоту построим прямоугольник с площадью . Тогда сумма площадей всех п прямоугольников (при достаточно большом п) дает площадь приближенно равную площади трапеции, т.е.
. Тогда сумма площадей всех п прямоугольников (при достаточно большом п) дает площадь приближенно равную площади трапеции, т.е.
 - формула прямоугольников (1)
- формула прямоугольников (1)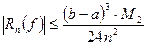 (2)
(2) (3)
(3) при п = 4, используя метод прямоугольников.
при п = 4, используя метод прямоугольников.
 =
=
 и
и  :
: 








 ,
,  ,
, 
 -по формуле прямоугольников
-по формуле прямоугольников 
 , тогда
, тогда  .
. или
или 
 Пусть на отрезке [a; b], где a < b, задана непрерывная функция f(x). Требуется вычислить интеграл
Пусть на отрезке [a; b], где a < b, задана непрерывная функция f(x). Требуется вычислить интеграл 

 где
где 

 - формула трапеций. (5)
- формула трапеций. (5)

 ,
, ,
, ,
, ,
, .
. ,
,  ,
,  ,
,  ,
,  .
.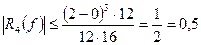

 -по формуле трапеций
-по формуле трапеций не отрезками прямых, как в методах прямоугольников и трапеций, а дугами парабол, то получим более точную формулу приближенного значения интеграла
не отрезками прямых, как в методах прямоугольников и трапеций, а дугами парабол, то получим более точную формулу приближенного значения интеграла  Предварительно найдем вспомогательную площадь S криволинейной трапеции, ограниченной сверху параболой y = ax2 + bx + c, прямыми x = -h, x = h и отрезком [ -h; h ].
Предварительно найдем вспомогательную площадь S криволинейной трапеции, ограниченной сверху параболой y = ax2 + bx + c, прямыми x = -h, x = h и отрезком [ -h; h ]. (6)
(6)

 . Подставляя полученные значения в (7) получим:
. Подставляя полученные значения в (7) получим: - формула Симпсона для рис 3.3 (8)
- формула Симпсона для рис 3.3 (8)
 (9)
(9) 
 и т. д. до
и т. д. до
 =
=
 и
и 
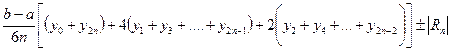 (10)
(10) где
где  (11)
(11) , f (x)= x3
, f (x)= x3















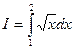 , разбив интервал интегрирования на 10 частей. Оценить погрешность.
, разбив интервал интегрирования на 10 частей. Оценить погрешность. )
) )
) , с точностью до 0,001
, с точностью до 0,001 )
) , с точностью до 0,0001
, с точностью до 0,0001 )
) , с точностью до 0,01
, с точностью до 0,01 )
) , с точностью до 0,01
, с точностью до 0,01 )
) , с точностью до 0,01
, с точностью до 0,01 )
) , с точностью до 0,01
, с точностью до 0,01 )
)


