
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Краткий курс лекций и практическихСодержание книги Поиск на нашем сайте
ЮЖНО-ЯКУТСКИЙ ТЕХНОЛОГИЧЕСКИЙ КОЛЛЕДЖ Краткий курс лекций и практических Заданий по предмету «Численные методы». учебно-методические материалы для самостоятельной работы студентов гуманитарных и технических специальностей Г. Данные учебно-методические материалы предназначены для самостоятельной подготовки студентов гуманитарных и технических специальностей по следующим вопросам численных методов: приближенное решение уравнений, интерполирование функций, приближенные вычисления определенных интегралов, приближенное решение дифференциальных уравнений. Пособие представляет обобщенное изложение материала по предмету и включает в себя теоретические сведения, типовые задачи с подробными решениями и упражнения, выполнение которых будет способствовать усвоению теоретических положений численных методов и приобретению практических навыков использования различных методов и формул приближенных вычислений. Составители:
Яковенко Л. В., преподаватель математических дисциплин АУ РС(Я) ЮЯТК
Рецензент:
Утверждено:
Содержание
ГЛАВА 1 ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ. Отделение корней уравнения. Корнем уравнения f (x) = 0 (1) называется такое значение х = х0 при котором уравнение (1) превращается в тождество: f (x0 ) = 0 Корень уравнения геометрически представляет собой абсциссу точки пересечения, касания или другой общей точки графика функции у = f(x) и оси ОХ (рис.1.1).
Отделить корень уравнения – значит найти такой конечный промежуток, внутри которого имеется единственный корень данного уравнения. Отделение корней Графический метод отделения корней. Отделение корней уравнения (1) можно выполнить графически, построив график функции у = f(x), по которому можно судить о том, в каких промежутках находится точка пересечения его с осью ОХ. В некоторых случаях целесообразно представить уравнение f(x)=0 в виде: f1(x) = f2(x) (2) с таким расчетом, чтобы графики функций у = f1(x) и у = f2(x) строились по возможности проще. Корень уравнения (2) представляет собой абсциссу точки пересечения графиков у = f1(x) и у = f2(x). Таким способом можно найти, например, корни уравнения х3 + px + q = 0; это будут точки пересечения кубической параболы у = х3 и прямой у = - px – q. Решение. Имеем f(x) = х3 + х2 -11,
Искомый корень принадлежит промежутку (1,9; 1,94). f(1,9)= -0,531, f(1,94) =0,065, Следовательно,
Так как значения х21 и х22 , вычисленные с точностью до 0,001, совпали, то приближенным значением корня будет 1,936. Метод итераций. Если каким нибудь способом получено приближенное значение х0 корня уравнения, то уточнение приближения можно осуществить методом итераций (методом последовательных приближений). Пусть задано уравнение f(x) = 0, представим его в виде Пределом последовательности х1, х2, х3,..... хп .... является единственный корень уравнения f(x) = 0 на отрезке [a; b]. Пример 1.5: Способом итераций найти приближенное значение корня уравнения 2 – lgx – x = 0 с точностью до 0.001 Решение. Найдем интервал изоляции действительного корня уравнения. Представим уравнение в виде: lgx = – x + 2 Построим графики функций у = lgx и у = – x + 2. Точка М пересечения графиков имеет абсциссу в промежутке [1; 2]. Пусть х0 = 1. Запишем исходное уравнение в виде х = 2 – lgx.
Найдем приближения:
Таким образом, искомый корень с точностью до 0,001 равен 1,755 Упражнения. Отделить корни уравнения графически и методом исследования отрезков.
Решить способом хорд и касательных с точностью до 0,01 следующие уравнения:
Применив комбинированный способ хорд и касательных решить уравнение.
Решить способом итераций с точностью до 0,01 следующие уравнения.
ГЛАВА II. ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ. Пример 2.1 Составить полином Лагранжа, удовлетворяющий таблице1 значений Таблица 1
Решение. Вспомогательная функция Вычислим -сначала найдем производную
-затем вычислим Тогда по формуле (1)
= х + 1 Таким образом, в данном случае в качестве интерполяционного полинома найдена линейная функция f (x) = х + 1. Упражнения.
(Ответ: у =
(Ответ: у =
(Ответ: у =
(Ответ: у =2х - 1)
lg 2,0 = 0,30103, lg 2,1 = 0,32222, lg 2,2 = 0,34242, lg 2,3 = 0,36173, lg 2,4 = 0,38021, lg 2,5 = 0,39794. Пользуясь интерполяционной формулой Ньютона, найти lg 2,03. (Ответ: lg 2,03 = 0,30750)
(Ответ: у = 4х2 - 7х+ 9)
(Ответ: у =8 + 4(х - 3) + (х – 3)(х - 2)+
(Ответ: у = х3 + х2 + х + 1) ГЛАВА III. Метод прямоугольников.
т.е.
Абсолютная погрешность метода определяется неравенством:
где Пример 3.1: Вычислить интеграл Решение.
= т.к.
Следовательно:
Пример 3.2: Зная, что погрешность метода прямоугольников при вычислении интеграла Решение. Используя формулу (2) получим Умножим правую и левую части неравенства на дробь т.е Метод трапеций. Формулу трапеций получают аналогично формуле прямоугольников: на каждом частичном отрезке криволинейная трапеция заменяется обычной.
Так как площадь криволинейной трапеции приблизительно равна сумме площадей трапеций Si, высота каждой из которых равна h, то:
Абсолютная погрешность метода (аналогично методу прямоугольников) составляет:
тогда Пример 3.3: Вычислить интеграл Решение. По формуле трапеций:
Тогда
Найдем погрешность:
Следовательно
§3. Метод парабол (Метод Симпсона). Если заменить график функции на каждом отрезке
Пусть парабола проходит через точки М1 (-h; у0), М2 (0; у1) и М3 (h; у2).
тогда полученная площадь:
(7) Выразим полученное значение через у0, у1 и у2. Используя формулы (6) получим c = y1,
Вывод формулы парабол (Симпсона). Пусть дана криволинейная трапеция, ограниченная функциями y = f (x), x = a, x = b, y = 0.
y = f (x): у0, у1, у2,......, у2п-2, у2п-1, у2п.
На отрезке [ x0; x2 ] парабола проходит через точки (х0; у0), (х1; у1), (х2; у2). Используя формулу (8) получим Аналогично на отрезке [ x2; x4 ]:
Следовательно:
Учитывая погрешность вычислений
Абсолютная погрешность метода оценивается соотношением:
Пример 3.4: Вычислить интеграл Решение. Количество разбиений 2п = 8, Составим таблицу:
Рассмотрим погрешность метода:
По формуле Симпсона получаем:
Точное решение: Упражнения.
(Ответ:
(Ответ:
(Ответ:
(Ответ: п = 10,
(Ответ: п = 5,
(Ответ: п = 4,
(Ответ: п = 4,
(Ответ: п = 6,
ГЛАВА IV. Метод Эйлера. Пусть требуется решить задачу Коши: найти решение дифференциального уравнения
удовлетворяющее начальному условию у(х0) = у0. При численном решении дифференциального уравнения (1) задача ставится следующим образом: в точках хк, х0, х1, х2,...., хп найти приближения Разность xk = x0 +kh где Метод Эйлера основан на непосредственной замене производной разностным отношением по приближенной формуле
Приближенное значение ук в точке xk = x0 +kh вычисляется по формуле:
Пример 4.1: Методом Эйлера найти значения решения уравнения Решение. По формуле (2) находим точки х0 = 1, х1 = 1,1, х2 = 1,2, х3 = 1,3, х4 = 1,4, х5 = 1,5. Значения искомой функции у = у(х), удовлетворяющей условиям данной задачи Коши, вычисляем по формуле (4). Результаты вычислений занесем в таблицу.
§2. Метод Рунге – Кутта. (Один из наиболее употребляемых методов повышенной точности). Пусть функция у определяется дифференциальным уравнением
Если положить
Получаем следующую схему вычислений:
Пример 4.2: Составь таблицу значений функции у, определяемой уравнением Решение. Используя формулы (5) найдем числа:
Отсюда Таким образом у1 = 1 + 0,1832 = 1,1832 при х = 0,2. По этой же схеме находим у2 и т.д. процесс вычисления ведем по схеме:
Упражнения. 1. Найти, используя метод Эйлера, значения функции у, определяемой дифференциальным уравнением
Ответ:
2. Найти по методу Эйлера четыре значения функции у, определяемой уравнением
Ответ:
3. Найти по методу Эйлера три значения функции у, определяемой уравнением
Ответ:
4. Найти по методу Эйлера четыре значения функции у, определяемой уравнением
Ответ:
5. Найти, используя метод Эйлера, значения функции у, определяемой дифференциальным уравнением
Ответ:
6. Найти методом Эйлера численной решение уравнения
Ответ:
7. По методу Рунге – Кутта проинтегрировать уравнение Ответ:
8. По методу Рунге – Кутта проинтегрировать уравнение Ответ:
9. По методу Рунге – Кутта проинтегрировать уравнение Ответ:
Литература.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 408; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.98.244 (0.01 с.) |

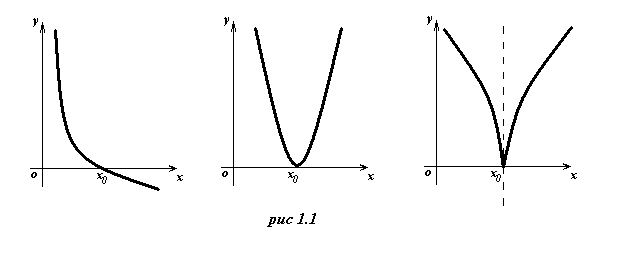
 =3х2+2х
=3х2+2х  = 6х+2. В указанном промежутке
= 6х+2. В указанном промежутке 




 , где
, где  <1 всюду на отрезке [a; b], содержащем единственный корень
<1 всюду на отрезке [a; b], содержащем единственный корень  . Исходя из некоторого начального значения
. Исходя из некоторого начального значения  можно построить последовательность:
можно построить последовательность:  ,
,  ,
,  .......
.......  ...
... = 2 – lgx,
= 2 – lgx, 

 в промежутке [1; 2], следовательно, способ итераций применим.
в промежутке [1; 2], следовательно, способ итераций применим.




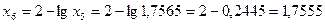


 последовательно при данных значениях хi:
последовательно при данных значениях хi: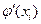 :
:  ,
,  ,
,  ,
, 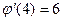 .
. =
= (х4 - 26х3 + 220х2 – 664х + 640))
(х4 - 26х3 + 220х2 – 664х + 640)) (- 2х3 -15х2 + 25х -9))
(- 2х3 -15х2 + 25х -9)) (х3 -13х2 + 69х -92))
(х3 -13х2 + 69х -92)) (х – 3)(х - 2)(х – 1) +
(х – 3)(х - 2)(х – 1) +  (х – 3)(х - 2)(х – 1)х, f(-0,5)= 0,700, f(2,5)= 5,658.)
(х – 3)(х - 2)(х – 1)х, f(-0,5)= 0,700, f(2,5)= 5,658.)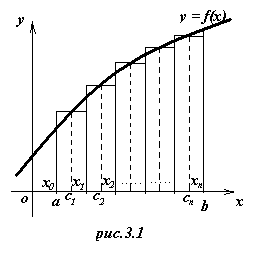 Пусть на отрезке [a; b], где a < b, задана непрерывная функция f(x). Требуется вычислить интеграл
Пусть на отрезке [a; b], где a < b, задана непрерывная функция f(x). Требуется вычислить интеграл  , численно равный площади соответствующей криволинейной трапеции. Разобьем основание этой трапеции на п равных частей длины
, численно равный площади соответствующей криволинейной трапеции. Разобьем основание этой трапеции на п равных частей длины  . тогда xi = x0+hi. В середине
. тогда xi = x0+hi. В середине  каждого такого отрезка построим ординату
каждого такого отрезка построим ординату  графика функции у = f(x). Приняв эту ординату за высоту построим прямоугольник с площадью
графика функции у = f(x). Приняв эту ординату за высоту построим прямоугольник с площадью . Тогда сумма площадей всех п прямоугольников (при достаточно большом п) дает площадь приближенно равную площади трапеции, т.е.
. Тогда сумма площадей всех п прямоугольников (при достаточно большом п) дает площадь приближенно равную площади трапеции, т.е.
 - формула прямоугольников (1)
- формула прямоугольников (1)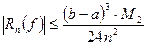 (2)
(2) (3)
(3) при п = 4, используя метод прямоугольников.
при п = 4, используя метод прямоугольников.
 =
=
 и
и  :
: 








 ,
,  ,
, 
 -по формуле прямоугольников
-по формуле прямоугольников 
 , тогда
, тогда  .
. или
или 
 Пусть на отрезке [a; b], где a < b, задана непрерывная функция f(x). Требуется вычислить интеграл
Пусть на отрезке [a; b], где a < b, задана непрерывная функция f(x). Требуется вычислить интеграл 

 где
где 

 - формула трапеций. (5)
- формула трапеций. (5)

 ,
, ,
, ,
, ,
, .
. ,
,  ,
,  ,
,  ,
,  .
.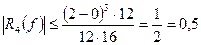

 -по формуле трапеций
-по формуле трапеций не отрезками прямых, как в методах прямоугольников и трапеций, а дугами парабол, то получим более точную формулу приближенного значения интеграла
не отрезками прямых, как в методах прямоугольников и трапеций, а дугами парабол, то получим более точную формулу приближенного значения интеграла  Предварительно найдем вспомогательную площадь S криволинейной трапеции, ограниченной сверху параболой y = ax2 + bx + c, прямыми x = -h, x = h и отрезком [ -h; h ].
Предварительно найдем вспомогательную площадь S криволинейной трапеции, ограниченной сверху параболой y = ax2 + bx + c, прямыми x = -h, x = h и отрезком [ -h; h ]. (6)
(6)

 . Подставляя полученные значения в (7) получим:
. Подставляя полученные значения в (7) получим: - формула Симпсона для рис 3.3 (8)
- формула Симпсона для рис 3.3 (8)
 (9)
(9) 
 и т. д. до
и т. д. до
 =
=
 и
и 
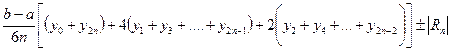 (10)
(10) где
где  (11)
(11) , f (x)= x3
, f (x)= x3















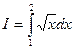 , разбив интервал интегрирования на 10 частей. Оценить погрешность.
, разбив интервал интегрирования на 10 частей. Оценить погрешность. )
) )
) , с точностью до 0,001
, с точностью до 0,001 )
) , с точностью до 0,0001
, с точностью до 0,0001 )
) , с точностью до 0,01
, с точностью до 0,01 )
) , с точностью до 0,01
, с точностью до 0,01 )
) , с точностью до 0,01
, с точностью до 0,01 )
) , с точностью до 0,01
, с точностью до 0,01 )
) (1)
(1) для значений точного решения у(хк)
для значений точного решения у(хк)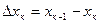 называется шагом сетки. Во многих случаях величину
называется шагом сетки. Во многих случаях величину  принимают постоянной. Пусть
принимают постоянной. Пусть  (2)
(2)  , где
, где  (3)
(3) - формула Эйлера (4)
- формула Эйлера (4) , для которого у(1) = 1, в пяти точках отрезка [ 1; 1,5 ], приняв h = 0,1.
, для которого у(1) = 1, в пяти точках отрезка [ 1; 1,5 ], приняв h = 0,1. с начальным условием у(х0) = у0. При численном интегрировании такого уравнения по методу Рунге – Кутта определяются четыре числа:
с начальным условием у(х0) = у0. При численном интегрировании такого уравнения по методу Рунге – Кутта определяются четыре числа: (5)
(5) , то можно доказать, что
, то можно доказать, что . (6)
. (6)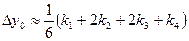











 , при начальном условии у(0) = 1, 0 ≤ х ≤ 1 при h = 0,2.
, при начальном условии у(0) = 1, 0 ≤ х ≤ 1 при h = 0,2.

 , при начальном условии у(0) = 1, принимая h = 0,1. Ограничиваясь отысканием первых четырех значений у.
, при начальном условии у(0) = 1, принимая h = 0,1. Ограничиваясь отысканием первых четырех значений у.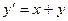 , при начальном условии у(0) = 1, принимая h = 0,1.
, при начальном условии у(0) = 1, принимая h = 0,1. , при начальном условии у(0) = 1, принимая h = 0,1.
, при начальном условии у(0) = 1, принимая h = 0,1. , при начальном условии у(0) = 0, принимая h = 0,1.
, при начальном условии у(0) = 0, принимая h = 0,1. , при начальном условии у(2) = 4, принимая h = 0,1. Ограничиваясь отысканием первых четырех значений у.
, при начальном условии у(2) = 4, принимая h = 0,1. Ограничиваясь отысканием первых четырех значений у. на отрезке [0; 1], при начальном условии у(0) = 1, принимая h = 0,2
на отрезке [0; 1], при начальном условии у(0) = 1, принимая h = 0,2 на промежутке [1; 2], при начальном условии у(1) = 0, принимая h = 0,1. В первых пяти точках.
на промежутке [1; 2], при начальном условии у(1) = 0, принимая h = 0,1. В первых пяти точках. на промежутке [0; 1], при начальном условии у(0) = 1, принимая h = 0,1. Вычисление вести с тремя верными знаками.
на промежутке [0; 1], при начальном условии у(0) = 1, принимая h = 0,1. Вычисление вести с тремя верными знаками. на промежутке [0; 1], при начальном условии у(0) = 1, принимая h = 0,1. Вычисление вести с двумя верными знаками.
на промежутке [0; 1], при начальном условии у(0) = 1, принимая h = 0,1. Вычисление вести с двумя верными знаками.


