Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
График квадратичной, кубической функции, график многочленаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Парабола. График квадратичной функции
Вспоминаем некоторые свойства функции Область определения – любое действительное число (любое значение «икс»). Что это значит? Какую бы точку на оси Область значений – это множество всех значений, которые может принимать переменная «игрек». В данном случае: Функция Функция При изучении пределов функций желательно понимать геометрический смысл предела. Я не случайно так подробно расписал свойства функции, все вышеперечисленные вещи полезно знать и помнить при построении графиков функций, а также при исследовании графиков функций. Пример 2 Построить график функции В этом примере мы рассмотрим важный технический вопрос: Как быстро построить параболу? В практических заданиях необходимость начертить параболу возникает очень часто, в частности, при вычислении площади фигуры с помощью определенного интеграла. Поэтому чертеж желательно научиться выполнять быстро, с минимальной потерей времени. Я предлагаю следующий алгоритм построения. Сначала находим вершину параболы. Для этого берём первую производную и приравниваем ее к нулю:
Если с производными плохо, следует ознакомиться с уроком Как найти производную? Итак, решение нашего уравнения:
Таким образом, вершина находится в точке Теперь находим другие точки, при этом нагло пользуемся симметричностью параболы. Следует заметить, что функция В каком порядке находить остальные точки, думаю, будет понятно из итоговой таблицы:
Данный алгоритм построения образно можно назвать «челноком». Возможно, не все врубаются в суть челнока, тогда для сравнения напоминаю известную телепередачу «туды-сюды с Анфисой Чеховой». Выполним чертеж:
Для квадратичной функции Если Если
Кубическая парабола Кубическая парабола задается функцией
Область определения – любое действительное число: Область значений – любое действительное число: Функция Функция Кубическую параболу тоже эффективнее строить с помощью
Наверняка, вы заметили, в чем ещё проявляется нечетность функции. Если мы нашли, что Теперь немного поговорим о графиках многочленов. График любого многочлена третьей степени
Многочлены 4-ой, 6-ой и других четных степеней имеют график принципиально следующего вида:
График функции Выполним чертеж:
Область определения: Область значений: То есть, график функции полностью находится в первой координатной четверти. Функция При построении простейших графиков с корнями также уместен поточечный способ построения, при этом выгодно подбирать такие значения «икс», чтобы корень извлекался нацело:
На самом деле хочется разобрать еще примеры с корнями, например,
График гиперболы Опять же вспоминаем тривиальную «школьную» гиперболу Выполним чертеж: Область определения: Область значений: Запись В точке Такая прямая (к которой бесконечно близко приближается график какой-либо функции) называется асимптотой. В данном случае ось Будет ГРУБОЙ ошибкой, если при оформлении чертежа по небрежности допустить пересечение графика с асимптотой. Также односторонние пределы Исследуем функцию на бесконечности: Таким образом, ось Функция График функции вида Если Если Пример 3 Построить правую ветвь гиперболы Используем поточечный метод построения, при этом, значения
Выполним чертеж:
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 1347; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.009 с.) |

 (
(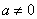 ) представляет собой параболу. Рассмотрим канонический случай:
) представляет собой параболу. Рассмотрим канонический случай: 

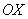 мы не выбрали – для каждого «икс» существует точка параболы. Математически это записывается так:
мы не выбрали – для каждого «икс» существует точка параболы. Математически это записывается так: 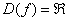 . Область определения любой функции стандартно обозначается через
. Область определения любой функции стандартно обозначается через  или
или  . Буква
. Буква  обозначает множество действительных чисел или, проще говоря, «любое икс» (когда работа оформляется в тетради, пишут не фигурную букву
обозначает множество действительных чисел или, проще говоря, «любое икс» (когда работа оформляется в тетради, пишут не фигурную букву  – множество всех положительных значений, включая ноль. Область значений стандартно обозначается через
– множество всех положительных значений, включая ноль. Область значений стандартно обозначается через  или
или  .
.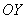 . Это очень полезное свойство, которое заметно упрощает построение графика, в чём мы скоро убедимся. Аналитически чётность функции выражается условием
. Это очень полезное свойство, которое заметно упрощает построение графика, в чём мы скоро убедимся. Аналитически чётность функции выражается условием  . Как проверить любую функцию на чётность? Нужно вместо
. Как проверить любую функцию на чётность? Нужно вместо подставить в уравнение
подставить в уравнение  . В случае с параболой проверка выглядит так:
. В случае с параболой проверка выглядит так:  , значит, функция
, значит, функция 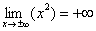 . Вот вам, кстати, и пример геометрического смысла предела функции: если мы будем уходить по оси
. Вот вам, кстати, и пример геометрического смысла предела функции: если мы будем уходить по оси  .
.
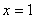 – именно в этой точке и находится вершина параболы. Рассчитываем соответствующее значение «игрек»:
– именно в этой точке и находится вершина параболы. Рассчитываем соответствующее значение «игрек»:



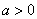 , то ветви параболы направлены вверх.
, то ветви параболы направлены вверх.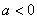 , то ветви параболы направлены вниз.
, то ветви параболы направлены вниз.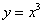 . Вот знакомый со школы чертеж:
. Вот знакомый со школы чертеж: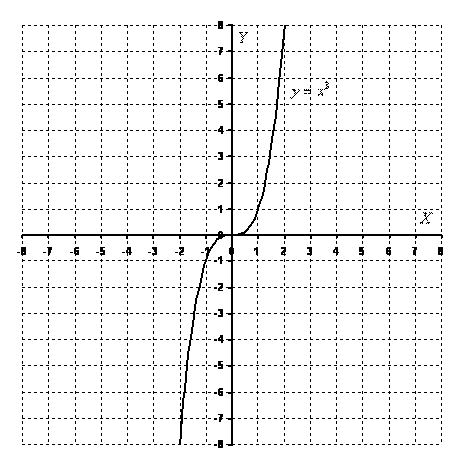
 .
.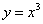 является нечётной. Если функция является нечётной, то ее график симметричен относительно начала координат. Аналитически нечётность функции выражается условием
является нечётной. Если функция является нечётной, то ее график симметричен относительно начала координат. Аналитически нечётность функции выражается условием 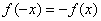 . Выполним проверку для кубической функции, для этого вместо «икс» подставим «минус икс»:
. Выполним проверку для кубической функции, для этого вместо «икс» подставим «минус икс»: 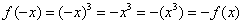 , значит, функция
, значит, функция  ,
, 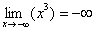

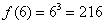 , то при вычислении
, то при вычислении 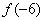 уже не нужно ничего считать, автоматом записываем, что
уже не нужно ничего считать, автоматом записываем, что  . Эта особенность справедлива для любой нечетной функции.
. Эта особенность справедлива для любой нечетной функции. (
(

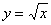

 .
.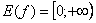 .
.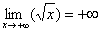

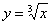 , но они встречаются значительно реже. Я ориентируюсь на более распространенные случаи, и, как показывает практика, что-нибудь вроде
, но они встречаются значительно реже. Я ориентируюсь на более распространенные случаи, и, как показывает практика, что-нибудь вроде 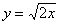 приходиться строить значительно чаще. Если возникнет необходимость выяснить, как выглядят графики с другими корнями, то, рекомендую заглянуть в школьный учебник или математический справочник.
приходиться строить значительно чаще. Если возникнет необходимость выяснить, как выглядят графики с другими корнями, то, рекомендую заглянуть в школьный учебник или математический справочник.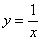 .
.
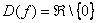 .
.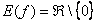 .
. обозначает: «любое действительное число, исключая ноль»
обозначает: «любое действительное число, исключая ноль»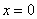 функция терпит бесконечный разрыв. Или с помощью односторонних пределов:
функция терпит бесконечный разрыв. Или с помощью односторонних пределов: 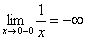 ,
, 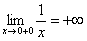 . Немного поговорим об односторонних пределах. Запись
. Немного поговорим об односторонних пределах. Запись 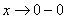 обозначает, что мы бесконечно близко приближаемся по оси
обозначает, что мы бесконечно близко приближаемся по оси 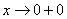 обозначает, что мы бесконечно близко приближаемся по оси
обозначает, что мы бесконечно близко приближаемся по оси 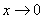 .
.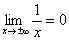 , то есть, если мы начнем уходить по оси
, то есть, если мы начнем уходить по оси 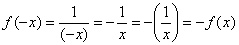 .
. (
(