
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение языка логики предикатов в математике и техникеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Как было показано в разд. 1 на соответствующих примерах, алгебра логики является основным теоретическим средством для построения цифровых автоматов и, в частности, электронных цифровых вычислительных машин. Именно благодаря алгебре логики стало возможным появление в 1945 г. первой электронной ЭВМ ЭНИАК. Логика предикатов пока такого широкого применения не нашла. Тем не менее, в самой математике она применяется для компактной записи определений, теорем и доказательств, а в технике может быть той благодатной почвой, на основе которой строятся системы искусственного интеллекта. Рассмотрим некоторые примеры использования языка логики предикатов в математике. Предварительно введем соглашение о том, что для большей ясности после кванторов Тогда определение предела числовой последовательности на языке логики предикатов запишется так:
Здесь использован трехместный предикат Определение возрастающей функции можно записать так:
Здесь использован двухместный предикат Рассмотрим записи некоторых теорем на языке логики предикатов:
Две теоремы, у которых условие первой является заключением второй, а условие второй является заключением первой, называются взаимно обратными друг другу. Так, теоремы (1) и (2), а также (3) и (4) – взаимно обратные теоремы. При этом если одну из них называют прямой теоремой, то вторая называется обратной. Две теоремы, у которых условие и заключение одной являются отрицанием соответственно условия и заключения другой, называются взаимно противоположными. Например, для теоремы (1) “Если в четырехугольнике диагонали равны, то четырехугольник является прямоугольником” обратной является теорема (2) “Если четырехугольник является прямоугольником, то его диагонали равны”. Для теоремы (1) противоположной является теорема (3) “Если в четырехугольнике диагонали не равны, то четырехугольник не является прямоугольником”, а для теоремы (2) противоположной является теорема (4) “Если четырехугольник не является прямоугольником, то его диагонали не равны”. В рассмотренном примере теоремы (1) и (4) являются одновременно ложными, а теоремы (2) и (3) – одновременно истинными. Контрпримером к теореме (1) является равнобочная трапеция.
Прямая и обратная теоремы в общем случае неравносильны, т.е. одна из них может быть истинной, а другая ложной. Однако можно легко показать, что теоремы (1) и (4), а также теоремы (2) и (3) всегда равносильны. Покажем это.
Из этих равносильностей следует, что если доказана теорема (1), то доказана и теорема (4), а если доказана теорема (2), то доказана и теорема (3). Значительный интерес представляет построение утверждения, отрицающего справедливость некоторой теоремы, если она может быть записана в таком виде:
Следовательно, чтобы доказать, что теорема
Очень часто при доказательстве теорем пользуются методом доказательства от противного. В этом случае предполагается, что теорема Если из последней формулы путем логических рассуждений приходят к неверному утверждению, то делается вывод о том, что исходная теорема верна. Таким образом, нужно противоположное высказывание свести к ложному и, пользуясь таблицей истинности для импликаций, из ложности посылки получить истинность исходного утверждения. А это возможно для импликации вида Таким образом, наши рассуждения мы можем записать следующим образом:
Этим самым мы доказываем, что наше предположение было неверным, т.е. теорема верна. Привести какие-то конкретные примеры применения языка логики предикатов вне сферы математики в ограниченном объеме учебного пособия довольно затруднительно. Это потребовало бы рассмотрения новых понятий, определений и постановок задач из различных предметных областей научной и практической деятельности человека. Поэтому ограничимся лишь некоторым иллюстративным описанием общего характера.
Как мы уже говорили, алгебра логики сыграла решающую роль в создании цифровых ЭВМ. Первые ЭВМ могли выполнять только арифметические действия над числами. Но человеку этого было мало. И уже практически сразу встал вопрос: а нельзя ли сделать ЭВМ усилителем интеллектуальных способностей человека? Иными словами, нельзя ли создать мыслящую машину? Чтобы решить эту глобальную проблему, человек должен был научить машину понимать естественный язык, чтобы он мог на нем общаться с машиной. Но чтобы этого достигнуть, процесс должен быть не односторонним (когда машину пытаются заставить понимать естественный язык), а двухсторонним (когда в естественном языке находят такие его особенности и законы, которые позволили бы формировать его и сделать науку о языке – лингвистику – не описательной, а точной). В начале XX века в нашей стране закладываются основы науки фонологии – науке о звуках языка, роль которой иногда сравнивают с ролью ядерной физики, сумевшей разложить казавшийся неделимым атом на частицы. Языковеды стали все шире применять в своих исследованиях методы математической статистики и теории вероятностей. В это же время датский ученый Луи Ельмслёв создал фундаментальный труд, перекинувший мост между наукой о языке и наукой о знаках – семиотикой. Семиотика же, в свою очередь, в поисках строгого научного аппарата для описания знаковых систем все более сближалась с математической логикой. После появления ЭВМ, в определенный момент, совершенно неожиданно для лингвистики, она оказалась на самом переднем крае развития науки и техники. Именно лингвистика, наука о языке, должна была обеспечить общение человека с машиной на естественном человеческом языке. Казалось, что, создав “точную лингвистику”, основанную на точных количественных методах математики, удастся решить проблему “искусственного интеллекта”. Но, столкнувшись вплотную с проблемами автоматического перевода, создания информационных систем, диалога с компьютером, ученые поняли, насколько были наивны. Язык, при всей его кажущейся простоте и доступности, оказался неимоверно сложной системой. И тем не менее прогресс вообще, и в области искусственного интеллекта в частности, остановить невозможно. Для построения систем искусственного интеллекта необходимо, в первую очередь, уметь автоматизировать процесс логических рассуждений (т.е. наделить такой способностью ЭВМ). Без использования специального языка, на котором можно формулировать посылки и делать верные логические выводы, такую задачу решить, очевидно, невозможно. В настоящее время считается, что язык логики предикатов, являющийся важнейшей составной частью математической логики, представляет собой такую логическую систему, с помощью которой можно выразить большую часть знаний, относящихся к математике, а также к естественному разговорному языку. Логика предикатов содержит правила логического вывода, позволяющие делать верные логические построения новых утверждений, исходя из некоторого заданного множества утверждений. Благодаря своей общности и логической силе логика предикатов может претендовать на использование ее для машинного построения умозаключений.
Вопросы для самоконтроля 1. Дайте определение одноместного и двухместного предикатов. Приведите примеры. 2. Дайте определение тождественно истинного и тождественно ложного предикатов. 3. Что называетсяотрицанием предиката? 4. Как определяется конъюнкция и дизъюнкция двух предикатов? 5. Что называется областью определения и множеством истинности предиката? 6. Дайте определение импликации двух предикатов. 7. Дайте определение кванторной операции всеобщности. 8. Дайте определение кванторной операции существования. 9. Можно ли произвольно менять порядок следования кванторов в формулах? Если нет, то почему? 10. Как связана кванторная операция всеобщности с операцией конъюнкции? 11. Как связана кванторная операция существования с операцией дизъюнкции? 12. Какие выражения являются формулами логики предикатов? 13. Какие формулы логики предикатов называются равносильными? 14. Приведите две пары каких-нибудь равносильных формул. 15. Дайте определение предваренной нормальной формы. 16. Какие формулы относятся к категории выполнимых? 17. Какие формулы относятся к категории общезначимых?
|
|||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1121; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.242.56 (0.012 с.) |

 и
и  в соответствующей переменной в некоторых случаях будем указывать область ее определения, а также будем применять символ эквивалентности
в соответствующей переменной в некоторых случаях будем указывать область ее определения, а также будем применять символ эквивалентности 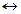 .
. .
.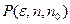 –
– 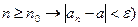 .
.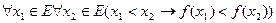 .
.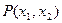 –
– 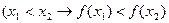
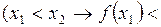
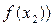 .
.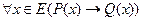 ; (1)
; (1)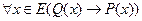 ; (2)
; (2)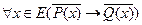 ; (3)
; (3)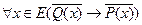 . (4)
. (4)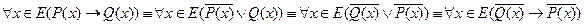 ;
;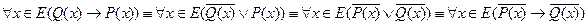 .
.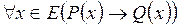 . Очевидно, что для опровержения этой теоремы необходимо доказать справедливость противоположного утверждения, т.е.
. Очевидно, что для опровержения этой теоремы необходимо доказать справедливость противоположного утверждения, т.е.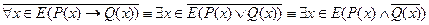 .
.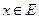 , для которого предикат
, для которого предикат 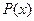 истинен, а предикат
истинен, а предикат 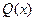 – ложен. Другими словами, нужно привести контрпример, опровергающий теорему
– ложен. Другими словами, нужно привести контрпример, опровергающий теорему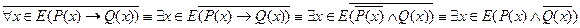 .
.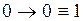 . В качестве первого
. В качестве первого 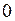 в данной импликации должна служить посылка
в данной импликации должна служить посылка 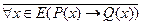 , второй
, второй 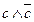 , а в качестве 1 должно получиться исходное утверждение, что и будет доказывать верность исходной теоремы.
, а в качестве 1 должно получиться исходное утверждение, что и будет доказывать верность исходной теоремы.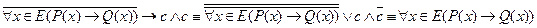 .
.


