
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логические операции над предикатамиСодержание книги
Поиск на нашем сайте Поскольку понятие предиката является обобщением понятия высказывания, то к ним применимы все операции логики высказываний. Рассмотрим логические операции на примерах одноместных предикатов. Пусть на некотором множестве Отрицанием предиката Из этого Конъюнкцией двух предикатов Множеством истинности предиката Дизъюнкцией двух предикатов Очевидно, что множеством истинности предиката Импликацией предикатов Множество истинности этой импликации определяется из следующих рассуждений: Так, для предикатов Упражнения 1. Среди следующих предложений выделить предикаты и для каждого из них указать множество истинности, если 1) 2) при 3) 4) существует такое число 5) 6) однозначное число 7) 8) 2. Выясните, какие из следующих предикатов являются тождественно истинными: 1) 4) 3. Пусть даны предикаты 1) 5) 4. Даны предикаты 1) 5. На множестве Найдите множества истинности следующих предикатов: 1) 5) 9)
Кванторные операции Кроме рассмотренных выше операций, общих как для алгебры логики, так и для логики предикатов, в последней используются логические операции, которые не применяются в алгебре логики. Эти операции превращают одноместный предикат в высказывание. Таких операций две. Они имеют собственное название и символически обозначаются с помощью так называемых кванторов (от лат. quantum − сколько) всеобщности и существования. Квантор всеобщности обозначается символом Предикаты могут быть как одноместными, так и многоместными, т.е. являются функцией одной или многих переменных, а каждый квантор должен выделять только одну переменную (относиться к одной переменной). Поэтому справа от символа квантора указывают переменную, которую квантор выделяет из предиката. Тогда кванторная операция всеобщности для одноместного предиката Рассмотрим теперь логический смысл, который придается кванторам всеобщности и существования. Квантор всеобщности. Пусть Переменную x в предикате Квантор существования. Пусть В предикате Рассмотрим пример использования кванторных операций. Пусть на множестве N задан предикат Очевидно, что первое из этих высказываний ложно, а второе истинно. Из определения кванторной операции всеобщности следует, что высказывание Кванторные операции применяются не только к одноместным, но и к многоместным предикатам. Так, например, если на множестве M задан двухместный предикат К этим предикатам можно применить кванторные операции по переменной y, которые приведут уже к четырем высказываниям (обратим внимание на то, что при первом применении кванторных операций по переменной
Кванторные операции можно менять местами. Тогда, если поменять местами кванторы, то получим еще четыре высказывания:
То есть для двухместного предиката применение двух кванторных операций дает восемь возможных высказываний. Рассмотрим пример конкретного предиката 1. 2. 3. 4. 5. 6. 7. 8. Анализируя приведенные высказывания, можно отметить, что высказывания 1, 5, 7 ложны, а высказывания 2, 3, 4, 6 и 8 истинны. Отсюда следует очень важный вывод, что в общем случае изменение порядка следования кванторов изменяет смысл высказывания (когда они применяются к многоместным предикатам), а значит, и его логическое значение (примером являются высказывания 3 и 7). Возникает естественный вопрос: связаны ли кванторные операции с какими-нибудь другими логическими операциями? Для ответа на этот вопрос рассмотрим предикат P(x), определенный на множестве Если же хотя бы для одного элемента
Нетрудно также показать, что справедлива равносильность
Отсюда можно сделать вывод, что кванторные операции являются обобщением операций конъюнкции и дизъюнкции на бесконечных областях. Интересно отметить, что перестановочное свойство кванторов отражает зависимость логического смысла предложений традиционной формальной логики (логики, в которой рассуждения, умозаключения и выводы осуществляются средствами естественного языка) от порядка расположения в них членов предложений. Рассмотрим два простых предложения, состоящих из одних и тех же членов, но имеющих различное местоположение. Вот эти предложения: “Они все там” и “ Там все они”. Под словами “они” и “все” мы будем полагать некоторые множества (например, людей). Очевидно, что множество “все” либо полностью включает множество “они”, либо эти множества являются совпадающими. Другими словами, множество “они” является либо частью множества “все”, либо совпадает с ним, но никак не наоборот. Тогда первое предложение следует понимать так, что в некотором месте (т.е. “там”– на собрании, конференции, в правительстве и т.д.) присутствует или находится полный состав элементов множества “все”. Второе же предложение следует понимать так, что на некотором мероприятии находятся все, но из множества “они”. Таким образом, в соответствии с первым предложением на мероприятии находятся все элементы из множества “все”, а в соответствии со вторым предложением на мероприятии находятся все элементы из множества “они”, которое меньше или, по крайней мере, равно множеству “все”. А это не одно и то же. Приведем еще некоторые примеры, свидетельствующие о том, что логика рассуждений и их результаты зависят от особенностей языка, на котором они осуществляются. Так, например, слова страна, девочка и др. в русском языке являются словами женского рода, а слово дом – мужского рода. Те же слова das Land, das Madchen, das Haus и др. в немецком языке являются словами среднего рода (на это указывает артикль das). И таких примеров можно приводить множество. Из этого следует, что во всех странах, где говорят на разных языках, как бы существуют свои формальные логики. Математическая логика как раз и является тем средством, которое позволяет устранить множественность логик.
Упражнения 1. Даны предикаты P(x) – “ 1) 2. Пусть предикат 3. Установить, какие из следующих высказываний истинны, а какие ложны, если областью определения предикатов является множество всех действительных чисел R: 1) 3) 5) 6) 7) 8) 9)
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 2207; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.011 с.) |

 определены два одноместных предиката
определены два одноместных предиката  и
и  .
. называется новый предикат
называется новый предикат  , который принимает значение “истина” при всех значениях
, который принимает значение “истина” при всех значениях 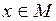 , при которых предикат
, при которых предикат  принимает значение “ложь”, и принимает значение “ложь” при тех значениях
принимает значение “ложь”, и принимает значение “ложь” при тех значениях 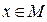 , при которых предикат
, при которых предикат  принимает значение “истина”.
принимает значение “истина”.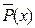 определения следует, что множеством истинности
определения следует, что множеством истинности  предиката является разность множеств
предиката является разность множеств  и
и  , где
, где 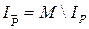 .
. и
и  называется новый предикат
называется новый предикат  , который принимает значение “истина” при тех значениях
, который принимает значение “истина” при тех значениях 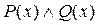 является общая часть множеств истинности предикатов
является общая часть множеств истинности предикатов  и
и  . Так, например, для предикатов
. Так, например, для предикатов  − четное число ” и
− четное число ” и  , конъюнкцией
, конъюнкцией 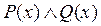 является предикат “
является предикат “  −четное число и
−четное число и 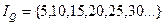 , то множество истинности
, то множество истинности 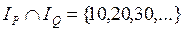 .
. и
и  называется новый предикат
называется новый предикат  , который принимает значение “ложь” при тех значениях
, который принимает значение “ложь” при тех значениях  и
и  , т.е.
, т.е.  . Так, для тех же предикатов, что и в выше приведенном примере, их дизъюнкцией
. Так, для тех же предикатов, что и в выше приведенном примере, их дизъюнкцией  .
. и
и  называется новый предикат
называется новый предикат  , который является ложным при тех значениях
, который является ложным при тех значениях  − значение “ложь” и принимает значение “истина” во всех остальных случаях.
− значение “ложь” и принимает значение “истина” во всех остальных случаях. следовательно
следовательно  .
. , импликацией
, импликацией 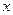 кратно 4, то
кратно 4, то  ,
, 
 ,то
,то  т.е. все натуральные числа.
т.е. все натуральные числа. (действительные числа) для одноместных предикатов и
(действительные числа) для одноместных предикатов и  для двухместных предикатов:
для двухместных предикатов: ;
; выполняется равенство
выполняется равенство  ;
; ;
; ;
;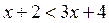 ;
;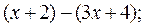

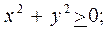 2)
2) 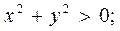 3)
3) 
 5)
5) 
 четное число” и
четное число” и  . Найти множества истинности предикатов:
. Найти множества истинности предикатов: ; 3)
; 3)  ; 4)
; 4) 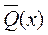 ;
; − “
− “ 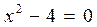 ” и Q (x) − “
” и Q (x) − “ 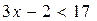 ”. Найдите множества истинности этих предикатов, если их область определения есть:
”. Найдите множества истинности этих предикатов, если их область определения есть: (действительные числа); 2)
(действительные числа); 2)  заданы предикаты:
заданы предикаты:  − “
− “ 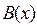 − “
− “  − “
− “  − “
− “  ; 2)
; 2) 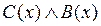 ; 3)
; 3) 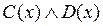 ; 4)
; 4)  ;
; ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8)  .
. 10)
10)  ; 11)
; 11)  .
. −перевернутая первая буква английского All − все, а квантор существования обозначается символом
−перевернутая первая буква английского All − все, а квантор существования обозначается символом  − перевернутая первая буква английского слова Exist − существует. Поскольку эти операции по смысловому содержанию квантора должны отвечать на вопрос “сколько?”, то, очевидно, должен следовать ответ “все” или “хотя бы один”, то и применяться они могут только к предикатам, являющихся по определению функцией некоторой переменной, принимающей, в общем случае, бесчисленное множество значений.
− перевернутая первая буква английского слова Exist − существует. Поскольку эти операции по смысловому содержанию квантора должны отвечать на вопрос “сколько?”, то, очевидно, должен следовать ответ “все” или “хотя бы один”, то и применяться они могут только к предикатам, являющихся по определению функцией некоторой переменной, принимающей, в общем случае, бесчисленное множество значений. записывается как
записывается как  , а кванторная операция существования для того же предиката ─ как
, а кванторная операция существования для того же предиката ─ как  .
. ,и ложным в противном случае. Это высказывание уже не зависит от x. Соответствующее ему словесное выражение будет “для всякого
,и ложным в противном случае. Это высказывание уже не зависит от x. Соответствующее ему словесное выражение будет “для всякого  .
. понимают высказывание, которое является истинным, если существует элемент
понимают высказывание, которое является истинным, если существует элемент  .
.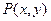 , то применение к этому предикату кванторных операций всеобщности и существования по переменной
, то применение к этому предикату кванторных операций всеобщности и существования по переменной  и
и  , зависящих от переменной
, зависящих от переменной  и не зависящих от переменной x.
и не зависящих от переменной x. ,
,  ,
,  ,
, 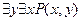 .
.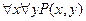 ,
,  ,
,  ,
,  .
. – “ x: y ”, определенного на множестве N. Для всех восьми возможных высказываний запишем их словесную формулировку и определим их логические значения.
– “ x: y ”, определенного на множестве N. Для всех восьми возможных высказываний запишем их словесную формулировку и определим их логические значения. . Если предикат P(x) является тождественно истинным, то истинными будут высказывания
. Если предикат P(x) является тождественно истинным, то истинными будут высказывания  . При этом истинными будут высказывания
. При этом истинными будут высказывания  и конъюнкция
и конъюнкция  .
.
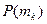 окажется ложным, то ложными будут и высказывания
окажется ложным, то ложными будут и высказывания 
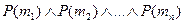 .
. .
. ” и
” и 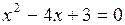 ”. Требуется определить, какие из высказываний истинны, и какие ложны:
”. Требуется определить, какие из высказываний истинны, и какие ложны: , 3)
, 3)  , 4)
, 4)  .
. – “ x: y ” определен на множестве
– “ x: y ” определен на множестве  . Показать, что высказывания
. Показать, что высказывания  и
и  имеют различные логические значения.
имеют различные логические значения.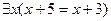 ; 2)
; 2)  ;
; ; 4)
; 4) 
 ;
;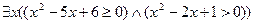 ;
;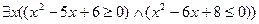 ;
; ;
; ;
; .
.


