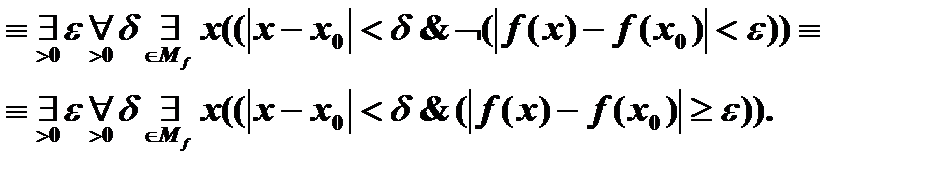Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практическое занятие № 13. Применение логики предикатовСодержание книги
Поиск на нашем сайте
Язык логики предикатов удобен для записи математических предложений и определений. Он дает возможность выражать логические связи между понятиями, записывать определения, теоремы, доказательства. Примеры выполнения заданий Запишите определение на языке логики предикатов, используя ограниченные кванторы, и постройте его отрицание: Функция f непрерывна в точке x0, если и только если для всякого положительного числа e существует положительное число d такое, что для всякого x из области определения D функции f, если |x - x0| < d, то Решение. Запишем это определение на языке логики предикатов двумя разными способами. 1 способ:
2 способ, используя ограниченные кванторы:
Построим отрицание этого определения:
Задания для самостоятельного выполнения
1. Запишите аксиомы положительных величин на языке логики предикатов, используя ограниченные кванторы:
0) Коммутативность сложения Для любых двух величин a, b Î A справедливо a + b = b + a. 1) Ассоциативность сложения Для любых двух величин a, b, с Î A справедливо a + (b + c) = (a + b) + c. 2) Монотонность сложения Для любых двух величин a, b Î A справедливо a + b > a. 3) Транзитивность отношения Для любых трех величин a, b, с Î A. Если a < b и b < c, то a < c. 4) Возможность суммирования Для любых двух величин a, b, с Î A существует однозначно определенная величина c = a + b. 5) Возможность вычитания Для любых двух величин a, b, с Î A если a > b, то существует одна и только одна величина c Î A, для которой b + c = a. 6) Возможность деления Какова бы ни была величина a Î A и натуральное число n, найдется такая величина b Î A, что n * b = a. 7) Возможность сравнения Для любых двух величин a, b Î A имеет место одно из трех отношений: 8) Аксиома Архимеда или Евдокса Каковы бы ни были величины a, b Î A, существует такое n, что n* b > a 9) Аксиома соизмеримости отрезков Пусть последовательность величин ai Î A, i = 1…n обладает свойством Пусть для любого e > 0 существует такое N(e), что при всех n > N разность |an – bn| < e. Тогда существует единственный элемент cÎ A, удовлетворяющий условиям ai < с, с < bj для любых i, j Î N.
2. Подберите элементарные предикаты и запишите следующие высказывания: 0) a) каждое положительное действительное число является квадратом другого; b) натуральное число, которое делится на 6, разделится и на 2; 1) a) для каждого натурального числа существует одно и только одно число, непосредственно следующее за ним; b) каждое действительное число является кубом другого; 2) a) натуральное число, которое делится на 6, разделится и на 3; b) произведение двух натуральных чисел, одно из которых четное, другое нечетное, есть число четное; 3) a) от перемены мест сомножителей произведение не меняется; b) натуральное число, которое делится на 2 и 3, разделится на 6; 4) a) натуральное число, которое делится на 9, разделится на 3; b) от перемены мест слагаемых сумма не меняется; 5) a) частное от деления двух натуральных четных чисел, если оно существует, есть число четное или нечетное; b) если произведение двух натуральных чисел делится на 5, то хотя бы один из сомножителей делится на 5; 6) a) для чисел отличных от нуля существует наибольший общий делитель; b) если произведение двух натуральных чисел делится на 12, то среди них есть четное число, делящееся на 3; 7) a) если произведение двух натуральных чисел делится на 18, то хотя бы один сомножитель делится на 6 или хотя бы один из сомножителей нечетный; б) сумма двух натуральных чисел, имеющих различную четность, нечетна; 8) a) для чисел отличных от нуля существует наименьшее общее кратное; б) если ни одно из двух натуральных чисел не делится на 11, то их произведение не делится на 11; 9) а) если произведение двух натуральных чисел делится на 12, то хотя бы один из сомножителей делится на 3 или хотя бы один из сомножителей четный; б) сумма двух натуральных четных чисел, есть число четное.
Рекомендуемая литература
[1] Самая популярная формулировка принципа Дирихле звучит так: "Если в n клетках сидит n+1 или больше зайцев, то найдётся клетка, в которой сидят, по крайней мере, два зайца". [2] Гранью в плоском представлении графа называется часть плоскости, ограниченная простым циклом и не содержащая внутри других циклов.
|
|||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1203; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.63.107 (0.01 с.) |

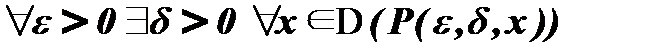 , где
, где