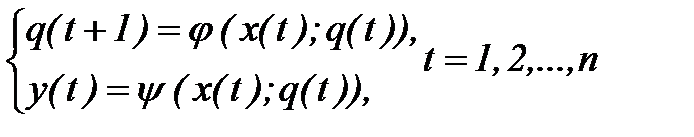Заглавная страница
Избранные статьи
Случайная статья
Познавательные статьи
Новые добавления
Обратная связь

ТОП 10 на сайте

Приготовление дезинфицирующих растворов различной концентрации

Техника нижней прямой подачи мяча.

Франко-прусская война (причины и последствия)

Организация работы процедурного кабинета

Смысловое и механическое запоминание, их место и роль в усвоении знаний

Коммуникативные барьеры и пути их преодоления

Обработка изделий медицинского назначения многократного применения

Образцы текста публицистического стиля

Четыре типа изменения баланса

Задачи с ответами для Всероссийской олимпиады по праву

Мы поможем в написании ваших работ!

ЗНАЕТЕ ЛИ ВЫ?

Влияние общества на человека

Приготовление дезинфицирующих растворов различной концентрации

Практические работы по географии для 6 класса

Организация работы процедурного кабинета

Изменения в неживой природе осенью

Уборка процедурного кабинета

Сольфеджио. Все правила по сольфеджио

Балочные системы. Определение реакций опор и моментов защемления

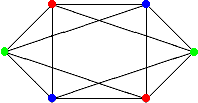
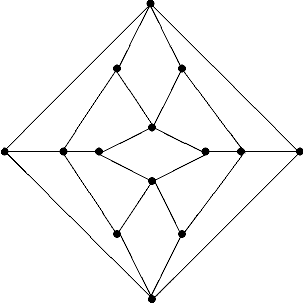
Главная Избранные Случайная статья Познавательные Новые добавления Обратная связь FAQ

Докажите, что граф, имеющий 10 вершин, степень каждой из которых равна 5, - не плоский.

⇐ ПредыдущаяСтр 6 из 9Следующая ⇒

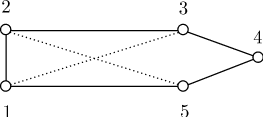
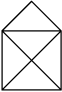
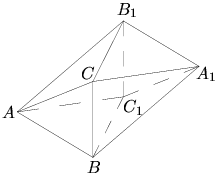
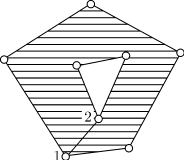
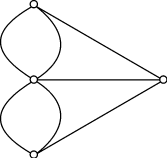
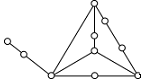
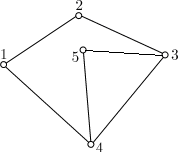
Решение:

Не выполняется неравенство 3 V - 6 ≥ E.

Семиугольник разбит на выпуклые пяти- и шестиугольники, причем так, что каждая его вершина является вершиной по крайней мере двух многоугольников разбиения. Докажите, что число пятиугольников разбиения не меньше 13.

Решение:

Докажите сначала неравенство E £ 3V - 6, используя то, что из каждой вершины выходит по крайней мере 3 ребра. Обозначим количество пятиугольников через a, количество шестиугольников через b.

Заметим, что 5a + 6b + 7 = 2E £ 6F – 12 = 6(a + b + 1) – 12. Отсюда a ³ 13.

4. Граф задан геометрически. А) Определите, содержит ли данный граф гамильтонов цикл? Б) Выпишите гамильтонов цикл у данного графа, если он есть:

Решение:

А) да, содержит, т.к. граф – полный и не содержит перекладин и висячих вершин.

Б) гамильтонов цикл выделен сплошной линией: (1,2), (2,3), (3,4), (4,5), (5,1).

Задания для самостоятельного выполнения

Запишите: 1) любой путь, не являющийся цепью; 2) цепь и простую цепь; 3) цикл, простой цикл, если таковые имеются.

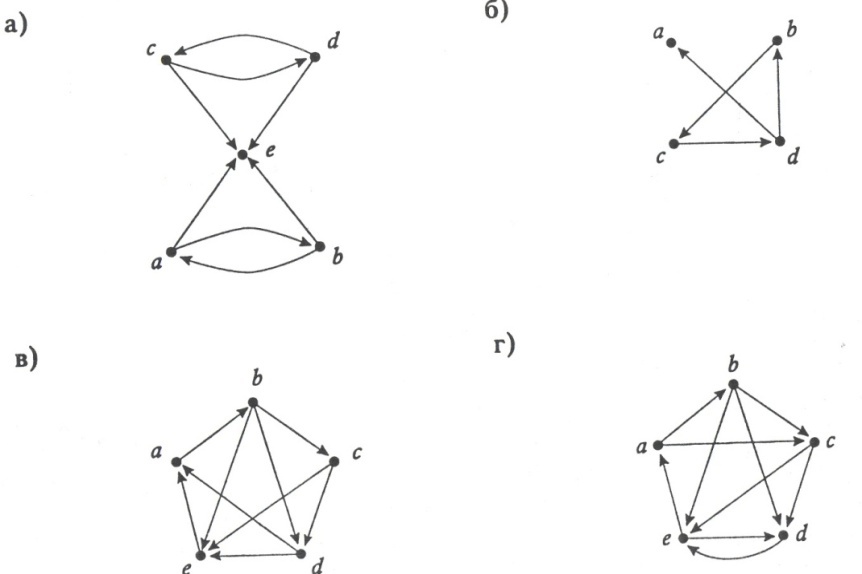
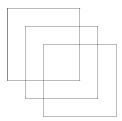
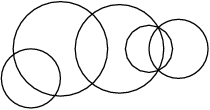
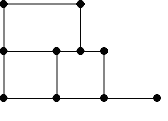
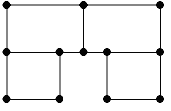
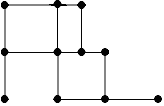
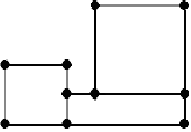
Можно ли нарисовать картинки, не отрывая карандаша от бумаги и проводя каждую линию ровно один раз? Какие из них являются эйлеровыми графами?

0)	1)	2)
3)	4)	5)
6)	7)
8)	9)

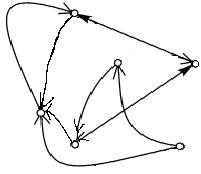
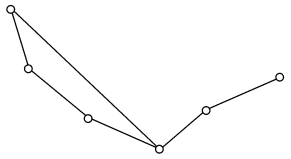
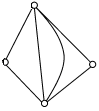
3. Граф задан геометрически. Выпишите гамильтонов цикл у данного графа, если он есть:

0) Решение:	1) Решение:
2) Решение:	3) Решение:
4) Решение:	5) Решение:
6) Решение:	7) Решение:
8) Решение:	9) Решение:

Практическое занятие №9. Автоматы

Система A=(X;Q;Y;j;y) называется конечным автоматом,
где

X = {a1,…,am}	- входной алфавит с входными сигналами,
Q = {q1,…,qn}	- множество состояний,
Y = {b1,…,bp}	- выходной алфавит с выходными сигналами,
j: X ´ Q ® Q	- функция переходов, т.е. j(x, q) ÎQ "xÎX; "qÎQ,
y: X ´ Q ® Y	- функция выходов, т.е. y(x, q) Î Y "xÎX; "qÎQ.

Существуют следующие способы задания автоматов:

- с помощью таблицы. Функции j и y задаются таблицей, строки которой соответствуют буквам входного алфавита, а столбцы – состояниям. В пересечении строки a_j и столбца q_i помещается состояние
y (a_j, q_i), в которое переходит автомат из состояния q_i под воздействием входного символа a_j, и значение j (a_j, q_i), которое при этом появляется на выходе;

- в виде диаграммы. Состояния q_i изображаются на плоскости кружками, из которого проводится стрелка в q_u, если автомат, находящийся в состоянии q_i, при подаче некоторого входного символа может быть переведен в состояние q_u;

- совокупностью четверок вида: q_ia_j ® q_la_p,. Если на вход автомата, находящегося в состоянии q_i, в момент времени t подается символ a_j, то на выходе автомата в этот же момент времени появляется символ a_p, и в следующий момент времени t+1 автомат будет находиться в состоянии q_l.

- в виде системы булевых функций. Каждому q_j ÎQ взаимно-однозначно ставится в соответствие двоичная последовательность длины r - двоичный код a(q) = z₁z₂…z_r. Аналогично каждому a_iÎX и каждому b_k ÎY ставим взаимно-однозначно в соответствие двоичные последовательности b(a) = x₁x₂…x_k; g(b) = y₁y₂…y_s.В результате автомат будет задан системой булевых функций {j₁,j₂,…,j_r,y₁,y₂,…,y_s};

- в виде канонических уравнений. Если в момент времени t=1,2,… на вход автомата A=(X; Q; Y; j; y) последовательно подаются входные символы x(t)ÎX и при этом автомат находится в состоянии q(t)ÎQ, то под воздействием символа x(t) автомат перейдет в новое состояние q(t+1)ÎQ и выдаст выходной сигнал y(t). Величины x(t), y(t), q(t), q(t+1) связаны между собой следующими каноническими уравнениями:

К задачам теории автоматов относятся: задачи анализа и синтеза автоматов, задачи полноты, минимизации, эквивалентных преобразований автоматов и другие.

Задачи анализа автоматов

Задача анализа состоит в том, чтобы по заданному описанию автомата (или по неполным данным об автомате и его функционированию) задать его поведение и установить те или иные его свойства.

Примеры выполнения заданий

1. Работа автомата задана таблично и выдает на выходе символ “*”, всякий раз, когда во входном алфавите встречается цепочка из комбинаций символов 0, 1, 2. Опишите работу автомата с помощью совокупности четверок. X = {0, 1, 2}, Y = {0, 1, 2} и Q = {q₀, q₁, q₂, q₃}. Определите, что распознает автомат.

Символы алфавита	С о с т о я н и я
q₀	q₁	q₂	q₃
	q₁,1	q₂,1	q₀,0	q₀,0
	q₀,1	q₀,1	q₀,1	q₀,1
	q₀,2	q₀,2	q₃,1	q₀,*

Решение:

q₀0® q₁1 q₀1® q₀1 q₀2® q₀2

q₁0® q₂1 q₁1® q₀1 q₁2® q₀2

q₂0® q₀0 q₂1® q₀1 q₂2® q₃1

q₃0® q₀0 q₃1® q₀1 q₃2® q₀*

Автомат распознает цепочку вида: 1111*

2. Описание автомата - двоичного сумматора последовательного действия, задано с помощью совокупности четверок. X= {00, 01, 10, 11},
Y = {0, 1}, Q = {q₀, q₁}. Опишите работу автомата с помощью диаграммы.

q₀<0,0> → q₀0 q₀<0,1> → q₀1 q₀<1,0> → q₀1 q₀<1,1> → q₁0

q₁<0,0> → q₀1 q₁<0,1> → q₁0 q₁<1,0> → q₁0 q₁<1,1> → q₁1

Решение.

q₁

(00,0)Ú(01,1)Ú(10,1) (01,0)Ú(10,0)Ú(11,1)

(11,0)

q₁

q₀

(00,1)

Задания для самостоятельного выполнения

1. Работа автомата задана с помощью совокупности четверок и выдает на выходе символ “ * ”, всякий раз, когда во входной последовательности алфавита {a, b} встречается цепочка символов. Определите, что распознает автомат. Опишите работу автомата таблично.

0)

q₀b → q₀b q₀a → q₁a q₁b → q₂b q₁a → q₀b q₂b → q₃b q₂a → q₀b q₃b → q₀b q₃a → *

1)

q₀b → q₁b q₀a → q₀b q₁b → q₀b q₁a → q₂a q₂b → q₃b q₂a → q₀b q₃b → q₀b q₃a → *

2)

q₀a → q₁a q₀b → q₀a q₁a → q₂a q₁b → q₀a q₂a → q₀a q₂b → q₃b q₃a → q₀a q₃b → *

3)

q₀b → q₁b q₀a → q₀b q₁b → q₂b q₁a → q₀b q₂b → q₀b q₂a → q₃a q₃b → q₀b q₃a → *

4)

q₀a → q₁a q₀b → q₀a q₁a → q₂a q₁b → q₀a q₂a → q₃a q₂b → q₀a q₃a → q₀a q₃b → *

5)

q₀b → q₁b q₀a → q₀b q₁b → q₂b q₁a → q₀b q₂b → q₃b q₂a → q₀b q₃b → q₀b q₃a → *

6)

q₀a → q₀a q₀b → q₁b q₁a → q₀a q₁b → q₂b q₂a → q₀a q₂b → q₃b q₃a → q₀a q₃b → *

7)

q₀b → q₀b q₀a → q₁a q₁b → q₀b q₁a → q₂b q₂b → q₀b q₂a → q₃b q₃b → q₀b q₃a → *

8)

q₀a → q₁a q₀b → q₀b q₁a → q₀a q₁b → q₂b q₂a → q₃a q₂b → q₀b q₃a → q₀a q₃b → *

9)

q₀a → q₀a q₀b → q₁b q₁a → q₂a q₁b → q₀a q₂a → q₃b q₂b → q₀a q₃a → q₀a q₃b → *

Решение:

Символы алфавита С о с т о я н и я

q₀ q₁ q₂ q₃

a

b

2. Работа автомата задана таблично и выдает на выходе символ “&”, всякий раз, когда во входном алфавите встречается цепочка символов. Определите, что распознает автомат. Опишите работу автомата с помощью совокупности четверок.

0)

Символы входного алфавита Состояния

q₀ q₁ q₂ q₃

О q₀,О q₂,О q₀,О q₀,О

К q₁,К q₀,О q₀,О q₀,О

Т q₀,О q₀,О q₃,Т q₀&

1)

Символы входного алфавита Состояния

q₀ q₁ q₂ q₃

С q₀,С q₂,С q₀,С q₀,С

О q_1,О q₀,С q₀,С q₀,С

А q₀,С q₀,С q₃,А q₀&

2)

Символы входного алфавита Состояния

q₀ q₁ q₂ q₃

М q₀,М q₀,М q₃,М q₀&

А q₀,М q₂,А q₀,М q₀,М

С q₁,С q₀,М q₀,М q₀,М

3)

Символы входного алфавита Состояния

q₀ q₁ q₂ q₃

А q₀,А q₂,А q₀,А q₀,А

Д q₁,Д q₀,А q₀,А q₀,А

Р q₀,А q₀,А q₃,Р q₀&

4)

Символы входного алфавита Состояния

q₀ q₁ q₂ q₃

О q₀,О q₂,О q₂,О q₀,О

Р q₁,Р q₀,О q₂,О q₀,О

М q₀,О q₀,О q₃,М q₀&

5)

Символы входного алфавита Состояния

q₀ q₁ q₂ q₃

Р q₀,Р q₀,О q₃,Р q₀&

М q₁,М q₀,О q₀,О q₀,О

И q₀,Р q₂,И q₀,О q₀,О

6)

Символы входного алфавита Состояния

q₀ q₁ q₂ q₃

А q₀,А q₂,А q₀,А q₀А

П q₁,П q₀,А q₀,А q₀,А

Р q₀,А q₀,А q₃,Р q₀&

7)

Символы входного алфавита Состояния

q₀ q₁ q₂ q₃

М q₀,М q₀,М q₃,М q₀&

И q₀,М q₂,И q₀,М q₀,М

Р q₁,Р q₀,М q₀,М q₀,М

8)

Символы входного алфавита Состояния

q₀ q₁ q₂ q₃

Р q₀,Р q₀,Р q₃,Р q₀&

У q₀,Р q₂,У q₀,Р q₀,Р

Т q₁,Т q₀,Р q₀,Р q₀,Р

9)

Символы входного алфавита Состояния

q₀ q₁ q₂ q₃

Л q₀,Л q₂,Л q₀,Л q₀,Л

Т q₁,Т q₀,Л q₀,Л q₀,Л

Я q₀,Л q₀,Л q₃,Я q₀&

Решение:

q₀ → q₁ → q₂ → q₃ →

q₀ → q₁ → q₂ → q₃ →

q₀ → q₁ → q₂ → q₃ →

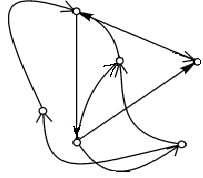
3. Работа автомата задана с помощью диаграммы и выдает на выходе символ “*", всякий раз, когда во входном алфавите встречается цепочка символов. Определите, что распознает автомат. Опишите работу автомата с помощью совокупности четверок.

0)

(б, б) (К, б) Ú (б, *)

q₀

q₁

(К, К)

1)

(м, м) (с, м) Ú (м, *)

q₀

q₁

(с, с)

2)

(б, б) (М, б) Ú (б, *)

q₀

q₁

(М, М)

3)

(г, г) (к, г) Ú (г, *)

q₀

q₁

(к, к)

4)

(б, б) (Г, б) Ú (б, *)

q₀

q₁

(Г, Г)

5)

(м, м) (д, м) Ú (м, *)

q₀

q₁

(д, д)

6)

(г, г) (м, г) Ú (г, *)

q₀

q₁

(м, м)

7)

(б, б) (Т, б) Ú (б, *)

q₀

q₁

(Т, Т)

8)

(а, а) (г, а) Ú (а, *)

q₀

q₁

(г, г)

9)

(м, м) (к, м) Ú (м, *)

q₀

q₁

(к, к)

Решение:

⇐ Предыдущая 1 2 3 4 567 8 9 Следующая ⇒

Поделиться:

Читайте также:

Психологические особенности спортивного соревнования

Приготовление дезинфицирующих растворов различной концентрации

Занятость населения и рынок труда

Социальный статус семьи и её типология

Последнее изменение этой страницы: 2016-09-19; просмотров: 727; Нарушение авторского права страницы; Мы поможем в написании вашей работы!

infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.31.240 (0.061 с.)