Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия Экология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления	Главная Избранные Случайная статья Познавательные Новые добавления Обратная связь FAQ Практическое занятие №8. Задачи оптимизации на графах. Эйлеровы и гамильтоновы графы. ⇐ ПредыдущаяСтр 5 из 9Следующая ⇒ Если дуге ориентированного графа G1 (V, E) поставлено в соответствие некоторое вещественное число a (u, v), называемое весом, то последовательность вершин v 0, v 1,..., vp определяет путь в G1 а его длина определяется как сумма весов: . Если в произвольном графе вес каждой дуги равен единице, то длина пути равна числу дуг. Задача о кратчайшем пути возникает чаще всего при решении транспортных и дискретных задач динамического программирования и др. Длину кратчайшего пути обозначают r (vi, vj) и называют расстоянием от vi до vj (расстояние может быть отрицательным). Для любого орграфа можно построить матрицу расстояний R=r (i, j). Заполняется матрица построчно, выбирая вершину слева (справа). Значением является наименьшее число дуг, связывающее вершину слева с одной из вершин строки. Если не существует ни одного пути из vi в vj, то полагаем r (vi, vj) = ¥. Если каждый контур нашего графа имеет положительную длину, то кратчайший путь будет всегда элементарным путем, т.е. в последовательности v 1,..., vp не будет повторов. Среднее отклонение вершины vi от центра графа D(vi) равно: , где m - число дуг в графе, v - пробегает вершины графа, n – количество вершин графа, i = 1..n. Вершина, для которой D(vi) окажется минимальным, называется центром графа (возможно несколько вершин – центр графа). Путем или маршрутом на графе G1(V,E) называется последовательность его вершин и ребер v1e1v2e2v3…vnen vn+1, в которой любые два соседних элемента инцидентны. Путь называется простым, если все ребра и все вершины на нем, кроме первой и последней, различны. Маршрут называется цепью, если все его ребра различные. Маршрут называется простой цепью, если все его вершины, а значит и ребра, различные. Циклом в графе называется путь, в котором начальная вершина совпадает с конечной и который содержит хотя бы одно ребро. Цикл называется простым, если в нем нет одинаковых вершин, кроме первой и последней, т.е. если все вершины различны. Если в графенет циклов, то он называется ациклическим. Теперь можно иначе определить понятие дерева. Связный граф без циклов называется деревом. Примеры выполнения заданий 7) 1.Орграф задан геометрически. Постройте матрицу расстояний. Вычислите центр орграфа. Решение: построим матрицу расстояний: R= r (i, j):
Общее число дуг m = 8. Рассчитываем отклонения от центра графа: D(1)=7/8; D(2)=D(3)=6/8=3/4; D(4)=10/8=5/4; D(5)=8/8=1.

Итак, центром графа являются вершины 2 и 3.

2. Посёлок построен в виде квадрата 3 квартала на 3 квартала (кварталы - квадраты со стороной b, всего 9 кварталов). Какой наименьший путь должен пройти асфальтоукладчик, чтобы заасфальтировать все улицы, если он начинает и кончает свой путь в угловой точке A? (Стороны квадрата - тоже улицы).

Решение: Понятно, что длина маршрута асфальтоукладчика не меньше 24, так как он должен проехать по каждой улице хотя бы один раз. Докажем, что по крайней мере по четырём улицам ему придётся проехать по два раза. Ровно на восьми перекрёстках пересекается нечётное число улиц.

Рис. 6. Кратчайший путь

Следовательно, любой кольцевой маршрут асфальтоукладчика должен проходить по два раза по крайней мере по 8/2 = 4 улицам. Минимальная длина маршрута асфальтоукладчика равна 28; один из возможных маршрутов приведён на рисунке 6.

Критерий эйлеровости графа

Связный неориентированный граф является эйлеровым тогда и только тогда, когда степени всех его вершин (валентность) – чётные числа.

Следовательно, замкнутую фигуру, в которой все вершины - четные, можно начертить одним росчерком без повторений, начиная обводить ее с любой точки.

Формула Эйлера: Для всякого плоского представления связного плоского графа без перегородок число вершин (V), число ребер (E) и число граней [2] с учетом бесконечной (R) связаны соотношением V – E + R = 2.

Связный орграф содержит эйлеров контур тогда и только тогда, когда для каждой вершины число входящих дуг равно числу выходящих.

Пример: эйлеровым графом может быть план выставки. Это позволяет так расставить указатели маршрута, чтобы посетитель смог пройти по каждому залу в точности по одному разу.

Гамильтоновой цепью называется простая цепь, содержащая все вершины графа. Гамильтоновым циклом называется простой цикл, содержащий все вершины графа.

Теорема Дирака: если в простом графе с n ³ 3 вершинами степень каждой вершины не меньше n/2, то такой граф обязательно будет гамильтоновым
(см. рис. 10).

Граф, который содержит простую цепь, проходящую через каждую его вершину, называется полугамильтоновым (см. рис. 11). На рис.12 приведен пример не гамильтонова графа.

Критерий же существования гамильтонова цикла в произвольном графе еще не найден.

Рис.10. Гамильтонов Рис.11. Полугамильтонов Рис.12. Не гамильтонов граф граф граф

Рассмотрим несколько достаточных условий существования гамильтоновых циклов в графе.

1) всякий полный граф является гамильтоновым. Действительно, он содержит такой простой цикл, которому принадлежат все вершины данного графа.

2) если граф, помимо простого цикла, проходящего через все его вершины, содержит и другие ребра, то он также является гамильтоновым.

Пример: если гамильтонов граф объединить с еще одной вершиной ребром так, что образуется висячая вершина, то такой граф гамильтоновым не является, поскольку не содержит простого цикла, проходящего через все вершины графа.

Не является гамильтоновым и граф, представляющий собой простой цикл с "перекладиной", на которой расположены одна или несколько вершин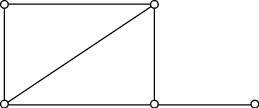

Примеры выполнения заданий

7)

1. Каждое ребро полного графа с 11 вершинами покрашено в один из двух цветов: красный или синий. Докажите, что либо "красный", либо "синий" граф не является плоским.