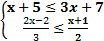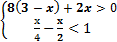Практическое занятие №10. Задачи синтеза автоматов

Задача синтеза автоматов состоит в построении автомата с наперед заданным поведением или функционированием.

Примеры выполнения заданий

1. Постройте конечный автомат, воспринимающий на входе двоичную последовательность и выдающий на выходе специальный символ
‘ *’, если во входной последовательности подряд встретится 4 единицы. В остальных случаях автомат на выходе повторяет входной символ.

Решение.

q00® q00 q01® q11

q10® q00 q11® q21

q20® q00 q21® q31

q30® q00 q31® q0*

 

2. Постройте конечный автомат таблично, представляющий двоичный сумматор последовательного действия.

Решение. Обозначим через q₀ и q₁ его состояния, соответствующие отсутствию и наличию переноса.

 

Символы алфавита	Состояния
x1	x2	q0	q1
		q0,0	q0,1
		q0,1	q1,0
		q0,1	q1,0
		q1,0	q1,1

Задания для самостоятельного выполнения

1. Постройте конечный автомат, выдающий на выходе символ “!”, всякий раз, когда во входной двоичной последовательности встречается:

0) последовательность 0000;

1) последовательность 1111;

2) последовательность 0110;

3) последовательность 0111;

4) последовательность 1000;

5) последовательность 0011;

6) последовательность 0010;

7) последовательность 1110;

8) последовательность 0001;

9) последовательность 1100.

2. Постройте конечный автомат, выдающий на выходе символ “♫”, всякий раз, когда во входной последовательности в алфавите

0) {А, н, ю, т} встречается имя “Анюта”;

1) {А, л, е, ш} встречается имя “Алеша”;

2) {И, р, н, а} встречается имя “Ирина”;

3) {С, а, ш} встречается имя “Саша”;

4) {Д, а, я, н} встречается имя “Даяна”;

5) {Н, и, а} встречается имя “Нина”;

6) {А, н, ж, е, л} встречается имя “Анжела”;

7) {А, н, т, о} встречается имя “Антон”;

8) {С, е, р, ж, а} встречается имя “Сережа”;

9) {Л, и, я} встречается имя “Лилия”.

 

С помощью совокупности четверок и диаграммы опишите работу автомата, представляющего троичный сумматор последовательного действия.

4. Постройте конечный автомат таблично, складывающий:

0)четные натуральные числа в D5;	1)нечетные натуральные числа в D8;
2)натуральные числа в D4;	3)нечетные натуральные числа в D6;
4)четные натуральные числа в D6;	5)нечетные натуральные числа в D5;
6)четные натуральные числа в D7;	7)натуральные числа в D3;
8)четные натуральные числа в D8;	9)нечетные натуральные числа в D7

Решение.

Символы алфавита	Состояния
x1	x2	q0	q1

Практическое занятие №11. Логика предикатов.

Предикатом арности n (n-арным, или n-местным предикатом) называют функцию от n переменных Q(x₁, x₂, …,x_n), определенную на декартовом произведении множеств: X₁´X₂´ …´X_n и принимающую значения из множества {И, Л}.

Примеры выполнения заданий

1. Постройте матрицу одноместного предиката Р(x), если:

P(x) = "x кратно 2", где xÎ [1, 14)

x

P(x)

Л

И

Л

И

Л

И

Л

И

Л

И

Л

И

Л

2. Изобразите геометрически множество истинности двуместного предиката P(x,y) = 1/4x ³ 1/4y”, если x, y Î (-2, 5];

Построим график прямой: 1/4y =1/4x; y = x; x y           Проверим точку выше графика прямой y = x, например, с координатами (-1; 2). Подставим координаты в неравенство: 1/4 (-1) ³ 1/4(2) – это ложно, поэтому

Y   0 X   -2 5   -2

область истинности предиката расположена ниже прямой, включая ее точки (т.к. нестрогое неравенство).

 

Задания для самостоятельного выполнения

1.Постройте матрицу одноместного предиката Q(x), если:

0) Q (x)=”2x^2 кратно 5”, xÎ (-8, 13);	1) Q (x)=”3x^2 кратно 2”, xÎ [-5, 13);
2) Q (x)=”4x^2 кратно 5”, xÎ (-10, 11);	3) Q (x)=”3x^3 кратно 2”, xÎ[-9, 10);
4) Q (x)=”5x^2кратно 3”, xÎ (-5, 13];	5) Q (x)=”3x^3 кратно 4”,xÎ(-7, 12);
6) Q (x)=”5x^3 кратно 4”, xÎ [-6, 14];	7) Q (x)=”x^4 кратно 2”, xÎ (-11, 1];
8) Q (x)=”x^3 кратно 5”, xÎ (-9, 10);	9) Q (x)=”x^2кратно 3”, xÎ [-7, 12);

 

x

Q(x)

2.Изобразите геометрически множество истинности одноместных предикатов G(x) и P(x), если:

0) G(x) = ”8 ³ -2x > 4/3”;	P(x) = ”2 >1/5x ³ -5”;
1) G(x) = ”-9 < -3x £ 3/2”;	P(x) = ”12 > 3/4x > -3”;
2) G(x) = ”0 ³ 1/3x >-5/9”;	P(x) = ”–14 £ -7x £ 1/4”;
3) G(x) = ”1/4 < -3x £ 9”;	P(x) = ”1 ³ 1/6x > -1/2”;
4) G(x) = ”1/3 > -6x >-6”;	P(x) = ”5 ³ 1/2x ³ -1/4”;
5) G(x) = ”8 ³ -2x > 4/3”;	P(x) = ”1/10 >1/5x > -5”;
6) G(x) = ”-1 < -3x £ 3/2”;	P(x) = ”6 > 1/4x > -3”;
7) G(x) = ”0 ³ 1/2x >-3/4”;	P(x) = ”–1 £ -7x £ 1/2”;
8) G(x) = ”1/5 < -3x £ 9”;	P(x) = ”1 ³ 1/6x > -1/2”;
9) G(x) = ”1/8 > -4x>-8”;	P(x) = ”2 ³ 1/2x ³ -1/4”;

 

X

0

X

3.Изобразите геометрически множество истинности предиката P(x), решив систему неравенств:

0) P(x)=	1) P(x)=
2) P(x)=	3) P(x)=
4) P(x)=	5) P(x)=
6) P(x)=	7) P(x)=
8) P(x)=	9) P(x)=

X

0

 

 

4. Постройте матрицу двуместного предиката P(x,y) и проверьте решение геометрически:

0)P(x,y)=”3x>-1/2y”, при x, y Î(-4,4);	1)P(x, y)=”1/3x > 9y”, при x, y Î (-2,5];
2)P(x,y)=”-1/4x£2y”, при x, y Î[-1,5];	3)P(x,y)=”10x£1/2y”, при x,y Î (-4,3);
4)P(x,y)=”5x>1/2y”, при x, y Î[-6,1);	5)P(x,y)=”-4x£2/3y”, при x, y Î [-5,1];
6)P(x,y)=”-1/10x£ 5y”, при x,y Î(-1,7)	7)P(x,y)=”3x£ 5/3y”, при x, y Î [-2,4];
8)P(x, y)=”-3x<2y”, при x, y Î [-5,2);	9)P(x,y)=”1/6x>-12y”, при x,y Î[-1,6).

x y

Y X