Решите задачу по вычислению валентности вершин графа

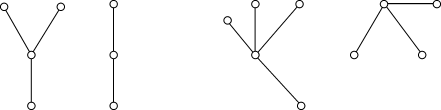
Школьник сказал своему приятелю: - У нас в классе 35 человек. Каждый из них дружит ровно с 11 одноклассниками... - Не может этого быть, - сразу ответил приятель, победитель математической олимпиады. Почему он так решил?

Решение: представим себе, что между каждыми двумя друзьями протянута ниточка. Тогда каждый из 35 учеников будет держать в руке 11 концов ниточек, и значит, всего у протянутых ниточек будет 11 35 = 385 концов. Но общее число не может быть нечётным, так как у каждой ниточки 2 конца.

4.Решите задачу по выявлению связности компонент графа

В компании из 7 мальчиков каждый имеет среди остальных не менее трех братьев. Докажите, что все семеро — братья.

Решение: возьмём любых двух мальчиков из этой компании. Предположим, что они не братья. Тогда каждый из них имеет среди оставшихся по три брата. По принципу Дирихле[1], у них есть общий брат, а значит, они братья. Итак, любые два мальчика из этой компании - братья, что и требовалось доказать.

Докажите, что граф с n вершинами, степень каждой из которых не менее (n - 1)/2, - связен.

Решение: рассмотрим две произвольных вершины и предположим, что они не соединены путем, то есть такой последовательностью ребер, в которой начало очередного ребра, совпадает с концом предыдущего. Каждая из этих двух вершин по условию соединена не менее, чем с (n - 1)/2 другими; при этом все упомянутые вершины различны - ведь если какие-то две из них совпадают, то есть путь, соединяющий исходные вершины. Таким образом, мы указали не менее
(n - 1)/2 + (n - 1)/2 + 2 = n + 1 вершин. Противоречие.

6.Определите, являются ли данные графы деревьями:

Ответ: да, все указанные графы являются деревьями согласно свойствам деревьев.

Задания для самостоятельного выполнения

 

 

1. Докажите, что валентности вершин графов А и Б совпадают.

А Б

2. Заданы два графа G₁(V₁, E₁) и G₂(V₂, E₂). Выясните, изоморфны ли графы?

3. Определите виды графов и подсчитайте валентность вершин:

0) Решение:	1) Решение:
2) Решение:	3) Решение:
4) Решение: А       С В	5) Решение: А В   С Д
6) Решение:	7) Решение: А В       С Д
8) Решение:	9) Решение: А В     С Д

4.Определите виды графов и подсчитайте валентность вершин:

 

 

0) Решение:	1) Решение:
2) Решение:	3) Решение:
4) Решение:	5) Решение:
6) Решение:	7) Решение:
8) Решение:	9) Решение:

 

Практическое занятие №7. Неориентированные графы

Неориентированный граф G (V, E) – непустое конечное множество узлов (вершин) V и набор неупорядоченных пар вершин (ребер) E.

Способы задания графа:

 

1) аналитический (в виде алгебраической системы);

2) геометрический (в виде произвольного рисунка);

3) матричный (в виде матриц смежности и инцидентности).

Пусть v ₁, v ₂,... v_n - вершины графа G (V, E), а e ₁, e ₂,... e_m - его ребра.

Матрицей смежности графа G называется матрица A(G)= || a_ij ||, i =1,..., n;
j = 1,..., n, у которой элемент a_ij равен числу ребер, соединяющих вершины v_i и v_j (соответственно, идущих из вершины v_i в вершину v_j).

 

Свойства матрицы смежности:

1) симметричная относительно главной диагонали,

2) значениями являются натуральные числа и ноль,

3) количество петель записывается на главной диагонали,

4) сумма значений по строке или в столбце равна валентности вершины.

Матрицей инцидентности для неориентированного графа с n вершинами и m ребрами называется матрица В(G) = [b_ij], i=1, 2,..., n, j = 1,2,..., m, строки которой соответствуют вершинам, а столбцы - ребрам. Элемент b_ij=1, если вершина v_i инцидентна ребру e_j и b_ij=0, если вершина v_i не инцидентна ребру e_j.

 

Свойства матрицы инцидентности:

1) несимметричная,

2) значениями являются ноль и единица,

3) сумма значений по строке или в столбце равна 2, если нет петель.

 

 

Примеры выполнения заданий

1. Граф G(V,E): V={a, b, c, d}, E={(a,b),(b,a),(b,c),(c,b),(a,c),(c,a),(c,d),(d,c)} задан как алгебраическая система. а) Выясните, является ли заданное отношение эквивалентным. б) Для приведенного отношения задайте граф геометрически. с) Постройте для графа матрицу смежности и матрицу инциденций.
Решение а): нарушено условие рефлексивности – отсутствуют: (а,а), (b,b), (c,c), (d,d), поэтому заданное отношение R не является эквивалентным.	Решение б): a d b c
Решение с): матрица смежности А(G)=	матрица инцидентности В(G)=   a b c d