Фундаментальное множество циклов графа

Предположим, нам нужно с помощью закона Кирхгофа составить систему линейных уравнений для электрической цепи. Цепь имеет сложную структуру и содержит большое количество циклов. Запишем закон Кирхгофа для каждого цикла и начнем решать полученную систему уравнений. Сразу обнаружится, что часть уравнений являются линейно зависимыми, т.е. получаются из других. Значит, какие-то циклы были не нужны?!

В этой главе будет доказано, что ЛЮБОЙ ЦИКЛ графа можно однозначно разложить по ФУНДАМЕНТАЛЬНЫМ ЦИКЛАМ этого графа так же, как любой вектор трехмерного пространства однозначно представляется линейной комбинацией базисных векторов i, j, k. Так же будет показано, как построить для данного графа это фундаментальное множество.

В дальнейшем под графом будем понимать связный неориентированный граф, под циклом — ЭЛЕМЕНТАРНЫЙ ЦИКЛ.

Вначале для произвольных множеств А и В введем операцию взятия СИММЕТРИЧЕСКОЙ РАЗНОСТИ А В=(А B)/(А В).

Рисунок 8.16

Построим симметрическую разность трех множеств. Выберем порядок действий, соответствующий следующей расстановке скобок: (A B) C.

Рисунок 8.17

В силу симметрии при любой расстановке скобок будет получаться то же множество A B C. Можно установить закономерность: в симметрическую разность входят элементы, содержащиеся одновременно либо в одном, либо в трех множествах, а принадлежащие двум — удаляются. Обобщим этот результат на произвольное число множеств.

УТВЕРЖДЕНИЕ 1.

Симметрическая разность множеств А₁, А₂, …, А_k содержит в точности те элементы, которые принадлежат НЕЧЕТНОМУ числу множеств.

Доказать это можно индукцией по числу множеств.

Вернемся к фундаментальным циклам. Это множество определяется через каркас графа.

Пусть уже построен каркас D =<V, T> графа G=<V, E>. Если к каркасу добавить произвольную хорду e (E\T), то получившийся граф (D e) будет содержать ровно один цикл. Назовем этот цикл С_е.

Рисунок 8.18

Добавляя к каркасу поочередно все хорды, получим ФУНДАМЕНТАЛЬНОЕ множество циклов Ф относительно каркаса D Ф ={C_е: e (E \ T)}.

?Вопрос 1. Укажите фундаментальное множество циклов графа G относительно каркаса D на рисунке 8.18.

Симметрическая разность любого числа циклов графа G является циклом графа G.

?Вопрос 2. В графе G (рисунок 8.18) найти C₁ C₂, если C₁=(1—2—3), C₂=(2—3—4).

Сформулируем без доказательства.

УТВЕРЖДЕНИЕ 2.

Произвольный цикл C графа G можно однозначно представить как симметрическую разность некоторого числа ФУНДАМЕНТАЛЬНЫХ ЦИКЛОВ.

Другими словами, любой цикл раскладывается по базису фундаментальных циклов.

Как уже говорилось, знание фундаментальных циклов имеет существенное значение при анализе ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ.

Для каждого фундаментального цикла данной цепи можно записать закон КИРХГОФА: сумма падений напряжений вдоль цикла равна 0. Все эти уравнения независимы, уравнения для остальных циклов будут следовать из них.

Опишем простой алгоритм построения фундаментальных циклов. Он основан на поиске в глубину из произвольного корня k и является рекурсивным. Каждая встреченная новая вершина v помещается в СТЕК и получает номер GLN [v] (порядок просмотра) и удаляется из него после использования. Поэтому СТЕК всегда содержит последовательность вершин от рассматриваемой в данный момент вершины v до корня k.

Анализируемое алгоритмом ребро (v—u) будет замыкать цикл, если (v—u) — хорда.

КРИТЕРИЙ ХОРДЫ следующий:

(v—u) будет хордой, если u — найденная соседка v — уже встречалась раньше при поиске в глубину. В этом случае она находится в СТЕКе и ее номер GLN (u) меньше соответствующего номера GLN (v). Но это еще не все. Если из u мы попали в вершину v, то есть u является отцом v, то GLN (u) < GLN (v), но (v—u) не хорда, а ветвь каркаса. Эту ситуацию легко распознать, так как в этом случае вершины u и v стоят в СТЕКе рядом.

Если же GLN (u) < GLN (v) и u не является отцом v, то (v—u) — хорда и цикл состоит из верхней группы элементов стека, начиная с v и кончая u.

Рисунок 8.19

Мы заранее знаем, что наибольшее число вершин, одновременно находящихся в стеке, не превышает n-длины пути от корня до самой удаленной вершины, поэтому СТЕК можно имитировать массивом переменной длины (длина его будет колебаться от 0 до n). Текущее значение длины будет храниться в переменной d, вталкивание в СТЕК вершины v будет изображаться: СТЕК[d]:=v, выталкивание верхушки СТЕКА: d:=d-1.

АЛГОРИТМ {Нахождение множества фундаментальных циклов графа}

Данные: Граф G=<V, E>, представленный списками ЗАПИСЬ[V], v V.

Результаты: Множество фундаментальных циклов Ф графа G.

Переменные: d, num, СТЕК, ЗАПИСЬ, GLN — глобальные.

1 procedure ЦИКЛ(v);

{находит фундаментальное множество циклов для компоненты связности графа, содержащей вершину v}

2 begin {ЦИКЛ(v)}

3 d:=d+1; СТЕК[d]:=v;

4 num:=num+1; GLN[v]:= num;

5 for u ЗАПИСЬ[v] do

6 if GLN[u]=0 then ЦИКЛ(u) {для новой вершины u}

7 else if (u<>СТЕК[d-1]) AND (GLN[u]<GLN[v]) then

{ребро (v-u) замыкает новый цикл}

8 выписать цикл с вершинами

9 СТЕК[d], СТЕК[d-1],.., СТЕК[c], где СТЕК[c]=u;

{конец цикла for — перебрали всех соседок v}

10 d:=d-1; {использованная v удаляется из СТЕКА}

11 end; {ЦИКЛ(v)}

1 begin {основная программа}

2 for v Є V do GLN[v]:=0;

3 num:=0; {инициализация перед началом нумерации}

3 d:=0; СТЕК[d]:=0; {d — число элементов в стеке}

4 for v V do

5 if GLN[v]=0 then ЦИКЛ(v)

6 end.

Оценим вычислительную сложность алгоритма.

Если отбросить число шагов, требующих выписывания всех фундаментальных циклов (строки 8–9), сложность имеет порядок О(n+m), как у всех алгоритмов, основанных на поиске в глубину.

Число шагов, потраченное на печать всех фундаментальных циклов, пропорционально суммарной длине всех циклов. Количество фундаментальных циклов = число всех хорд = m - (n - 1) = m - n +1. Длина любого цикла не превосходит n. Таким образом, суммарная длина всех циклов не превосходит n (m - n + 1) m n + n. Если отбросить случай, когда число ребер m=0, то сложность равна
О(mn).

Ответы.

Ответ 1. Ф = {C₁=(1—2—3), C₂=(2—3—4)}.

Ответ 2. С₁ С₂=(1—2—3—4).

8.6 Нахождение компонент двусвязности (блоков) графа

Если в связном графе найдутся две вершины u₁ и u₂ такие, что любой путь между ними будет проходить через вершину v, то вершина v будет называться ТОЧКОЙ СОЧЛЕНЕНИЯ.

Можно дать эквивалентное определение точки сочленения.

Вершина v графа G=<V, E> называется ТОЧКОЙ СОЧЛЕНЕНИЯ, если удаление этой вершины и всех, выходящих из нее ребер, ведет к увеличению компонент связности графа.

Если в связном (состоящем из 1 компоненты связности) графе нет точек сочленения, он — ДВУСВЯЗНЫЙ.

Любой МАКСИМАЛЬНЫЙ двусвязный подграф графа G называется КОМПОНЕНТОЙ ДВУСВЯЗНОСТИ или БЛОКОМ этого графа.

Рисунок 8.20

?Вопрос 1. Что будет являться пересечением двух различных блоков графа?

?Вопрос 2. Что произойдет с блоком, если к нему присоединить ребро графа, имеющего с блоком общую точку и не принадлежащее блоку?

Двусвязность графа — очень полезное свойство для некоторых прикладных задач.

Представим себе, что вершины графа — телеграфные станции; ребра — линии передач. Пусть одна из станций вышла из строя. Если граф двусвязный, то между любыми двумя оставшимися станциями сохранится связь.

Для многих задач важно знать блоки графа. Например, находить все элементарные циклы графа G можно ОТДЕЛЬНО для каждого блока графа G.

Нахождение точек сочленения и блоков графа — классическая задача. Будем искать точки сочленения, обходя все вершины графа методом поиска в глубину. Будем не только обходить вершины графа, но и строить его КАРКАС.

При построении каркаса поиском в глубину для двух вершин w и v, связанных ребром, всегда точно известно: или w — потомок v, или наоборот. Как распознать точку сочленения s, если уже построен каркас D графа G?

Вот КРИТЕРИЙ ТОЧКИ СОЧЛЕНЕНИЯ::

или это корень, имеющий не менее двух сыновей в D;

или у вершины s есть хотя бы один сын u такой, что ни он, ни его потомки не связаны хордами с предками s.

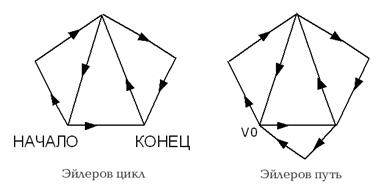
Рисунок 8.21

Рассмотрим рисунок 8.21. Номера вершин — номера, которые получают вершины графа во время построения каркаса. Покажем, что вершина s удовлетворяет второму условию критерия.

По построению каркаса s имеет сына: 3 и потомка 4. Предок s — вершина k. Сын 3 и его потомок 4 не связаны хордами с k. Итак, s — точка сочленения и граф G имеет блок 1={s—3, 3—4, s—4}.

?Вопрос 3. С какой вершиной нужно соединить вершину 4, чтобы граф G стал двусвязным?

Вершина k — точка сочленения, так как она корень, имеющая двух сыновей: s и 5. Поэтому граф G имеет блок 2 = {k—s} и блок 3 = {k—5}.

Зная критерий точки сочленения, опишем АЛГОРИТМ нахождения этих точек.

Пусть алгоритм поиска в глубину строит каркас D графа G. Для каждой вершины v будем вычислять два значения: GLN [v] и MIN [v].

G LN [v] — просто номер, который получает вершина при построении каркаса. Например, для корня GLN [k]=1.

Пусть вершина v соединена ХОРДАМИ (вспомните, что такое хорды для каркаса D!) c какими–то вершинами X₁, …, X_k. Выберем минимальный из номеров этих вершин:

X[v] = min { GLN [X₁], …, GLN [X_k]}.

?Вопрос 4. Какие вершины графа на рисунке 8.21 соединены хордами с вершиной s?

Пусть w — любой потомок вершины v. Он также может быть связан хордами с какими-то вершинами Y₁, …, Y_р.

Подсчитаем Y [w] = min { GLN [Y₁], …, GLN [Y_р]}.

И, наконец, подсчитаем Y[w] для КАЖДОГО w — потомка v и выберем из них минимальный.

Y [v] = min {Y[w], w — любой потомок v}

Минимальный из трех номеров { GLN [v], X[v], Y[v]} назовем MIN [v]:

MIN [v]= min { GLN [v], X[v], Y[v]}.

MIN [v] легко вычислить по индукции.

Пусть для всех сыновей U₁, …, U_k вершины v MIN [U₁], …, MIN [U_k] уже вычислены.

Тогда MIN[v] = min {GLN[v], X[v], MIN[u]},

где MIN[u]= min {MIN[U₁], …, MIN[U_k]}.

Вспомним критерий. Точка сочленения либо корень с двумя сыновьями, либо предки этой точки и потомки хотя бы одного сына не соединены хордами.

Запишем этот критерий через GLN и MIN.

МIN[u] —минимальный из номеров вершин, с которыми соединен сын u и его потомки. Если среди этих вершин не будет предков v, то критерий выполнится. Номера предков строго меньше GLN[v], поэтому MIN[u] ³ GLN [v] для некоторого сына u вершины v.

?Вопрос 5. Вычислите MIN[3] для сына 3 вершины s. Выполнится ли для s критерий?

АЛГОРИТМ {Нахождение компонент двусвязности графа}

Данные: Граф G = <V, Е> без изолированных вершин, представленный списками инцидентности ЗАПИСЬ[v], v Î V.

Результаты: Множество ребер всех компонент двусвязности. Переменные MIN, GLN, CTEK, num — глобальные.

1 procedure BLOC(v,p);

{поиск в глубину, начиная с v. в стек записываются
ребра блоков, p — отец v}

2 begin

3 num:=num+1; GLN[v]:=num; {нумеруем v}

4 MIN[v]:= GLN[v];

5 for u Є ЗАПИСЬ[v] do

6 if GLN[u]=0 then {u — новая, (v-u) — ветвь}

7 begin

8 СТЕК<= (v-u); {Ветвь поместили в стек, поиск
продолжается с u}

9 BLOC(u, v) {у u не осталось новых соседей,
был подсчитан MIN[u]. Пора
пересчитать MIN[v] и проверить
критерий}

10 MIN[v]:=min (MIN[v], MIN[u]);

11 if MIN[u] >= GLN[v] then

{v — точка сочленения. Ребра, занесенные в
стек последними до (v—u) включительно —
блок, связывающий u всех его потомков}

12 begin {печать ребер блока}

13 repeat

14 e<= СТЕК;

15 write(e);

16 until e=(v-u);

17 write(;) {знак конца блока}

18 end

19 end {if GLN[u]=0}

20 else {u — не новая}

21 if (u<>p) and (GLN[u] < GLN[v]) then

22 begin {условие хорды}

23 СТЕК <= (v-u);

{v соединена хордой с u, пересчитаем MIN[v]}

24 MIN[v]:=min (MIN[v], GLN[u])

25 end

26 end; {BLOC}

1 begin {основная программа}

2 for v Î V do

3 begin

4 GLN[v]:=0; MIN[v]:=n

5 end;

6 СТЕК:= NIL; num:=0;

7 BLOC(k,0);

8 end.

Алгоритм составлен. Осталось доказать его корректность.

Покажем, что вызов BLOC(v, 0) для любой вершины v графа приведет к печати всех блоков этого графа.

1. Если граф двусвязный, то он состоит из одного блока и не имеет точек сочленения. В строке 8 в стек будут заноситься все ветви каркаса, в строке 23 — хорды. Точек сочленения нет, поэтому критерий 11 выполнится первый раз для корня. К корню мы вернемся, рассмотрев все вершины и заслав в стек все ребра.

2. Пусть граф содержит i (i>1) блоков, а алгоритм исправно работает для любого графа, содержащего блоков < i-1.

Начинаем поиск в глубину и на каком-то шаге первый раз встретим ребро (v—u) такое, что MIN[u] ³ GLN[v] (критерий). V — корень или точка сочленения, u — сын вершины v. Так как проверка критерия выполнилась первый раз, то все потомки u рассмотрены и точек сочленения среди них нет. Следовательно, верхняя часть стека вплоть до ребра (v—u) — первый блок. Удалим этот блок, оставив только вершину v.

Запустим алгоритм для оставшегося графа. Единственным изменением в его работе будет следующее: когда v будет просмотрена первый раз, цикл 5 не будет перебирать вершины из удаленного блока.

В графе остался (i-1) блок, и по индуктивному предположению они будут найдены, а доказательство — окончено.

Оценим вычислительную сложность алгоритма.

Цикл 2 требует для n вершин О(n) шагов. Вызов BLOC(v, 0) повлечет О(n+m) шагов, где n и m — число вершин и ребер, т.к. столько требует поиск в глубину. Каждое ребро в цикле 13 удаляется из стека и выводится на печать ровно один раз, т.е. не более О(m) шагов. Сумма всех этих слагаемых не превосходит О(n+m) шагов.

Ответы.

Ответ 1. Точка сочленения или ничего.

Ответ 2. Максимальность блока означает, что, присоединяя к нему любой подграф, мы автоматически присоединяем точку сочленения.

Ответ 3. С вершиной 5.

Ответ 4. Вершина 4.

Ответ 5. MIN[3]=2, т.к. потомок 3 вершина 4 связана хордой с s, а GLN[s]=2. GLN[s]=MIN[3] и критерий выполнен.

Эйлеровы пути

ЭЙЛЕРОВЫМ ПУТЕМ в графе называется произвольный путь, проходящий через КАЖДОЕ ребро в точности ОДИН раз.

Если путь заканчивается в начальной вершине, то он называется ЭЙЛЕРОВЫМ ЦИКЛОМ.

Рисунок 8.22

Задача существования эйлерова пути в заданном графе была решена великим русским математиком ЛЕОНАРДОМ ЭЙЛЕРОМ в 1736 году.

Представленное им необходимое и достаточное условие существования такого пути считается первой в истории математики теоремой теории графов.

ТЕОРЕМА

Эйлеров путь существует тогда и только тогда, когда граф связный и содержит не более ДВУХ ВЕРШИН НЕЧЕТНОЙ СТЕПЕНИ. (Напомним, степень вершины — число смежных с нею ребер).

Заметим, что число вершин нечетной степени в любом графе всегда ЧЕТНО. Это легко доказать.

Просуммируем степени всех вершин графа. Эта сумма равна
2m — удвоенному числу ребер, т.к. каждое ребро соединяет две вершины. Вклад в эту сумму вершин четной степени — четен, поэтому вклад вершин нечетной степени тоже должен быть четен. Для этого их должно быть четное количество (нечетное число ребер четное число вершин = четный результат).

Новая формулировка теоремы:

ЭЙЛЕРОВ ПУТЬ В СВЯЗНОМ ГРАФЕ СУЩЕСТВУЕТ ТОГДА И ТОЛЬКО ТОГДА, ЕСЛИ ЧИСЛО ВЕРШИН НЕЧЕТНОЙ СТЕПЕНИ РАВНО 0 ИЛИ 2.

Докажем достаточность.

Если эйлеров путь существует, то нечетную степень имеют ровно две вершины — начало и конец. Если это цикл, то таких вершин — 0.

В дальнейшем будем рассматривать только эйлеровы циклы u, соответственно, графы без вершин нечетной степени. Если граф имеет 2 «нечетных» вершины, то добавим еще одну вершину и соединим ее ребрами с нечетными (см. рисунок 8.22). «Нечетные» вершины станут четными, эйлеров путь замкнется в цикл.

Поэтому достаточное условие сформулируем только для циклов:

ЕСЛИ В СВЯЗНОМ ГРАФЕ НЕТ ВЕРШИН НЕЧЕТНОЙ СТЕПЕНИ, В НЕМ СУЩЕСТВУЕТ ЭЙЛЕРОВ ЦИКЛ.

Доказательство будет следовать из анализа алгоритма его нахождения.

?Вопрос 1. Существует ли эйлеров цикл в данном графе:

Рисунок 8.23

АЛГОРИТМ. {Нахождение эйлерова цикла}

Данные: Связный граф G = <V, E> без вершин нечетной степени, представленный списками инцидентности ЗАПИСЬ[v], v Î V.

Результаты: Эйлеров цикл, хранящийся в стеке EC.

1 begin

2 СТЕК:=NIL; EC:=NIL;

3 k:= произвольная вершина G;

4 СТЕК<= k; {поместим k в СТЕК}

5 while СТЕК <> NIL do

6 begin

7 v:=top(CTEK); {верхний элемент СТЕКА}

8 if ЗАПИСЬ[v]<>0 then {ищем ребро,
выходящее из v}

9 begin

10 u:= первая вершина списка ЗАПИСЬ[v];

11 СТЕК <= u; {поместим u в СТЕК}

12 ЗАПИСЬ[v]:=ЗАПИСЬ[v] - [u];

13 ЗАПИСЬ[u]:=ЗАПИСЬ[u] - [v]; {удаляем ребро
(v-u) из графа G}

14 end {возврат на 5, теперь u — верхнии элемент}

15 else {из v не выходит ни одно ребро, путь
нельзя удлинить}

16 begin

17 v <= СТЕК; ЕС <= v {v выталкивается из СТЕКА
и помещается в ЕС}

18 end

19 end {пока СТЕК не пуст}

20 end.

Пусть k — вершина, выбранная в 3.

Цикл 5 начинает строить путь с началом в k, вершины этого пути помещаются в СТЕК, ребра удаляются из графа. Это продолжается до тех пор, пока не выполнится ЗАПИСЬ[v]= 0 в 15.

Это означает, что путь нельзя удлинить, он кончился на v. На самом деле v = k, т.к.иначе степень v была бы нечетной — зашли в v, но не вышли. Таким образом, мы вышли из k и вернулись в k т.е. описали цикл. Его вершины находятся в СТЕКЕ, ребра удалены из графа. Вершина k переносится из СТЕКА В ЕС, а «очередной» вершиной v становится верхний элемент СТЕКА.

Процесс повторяется, в СТЕК помещается некоторый цикл, проходящий через v, сама v переноситься в ЕС. По окончании работы СТЕК пуст, ЕС содержит эйлеров цикл.

На рисунке 8.24 изображен «модельный» граф, на котором удобно продемонстрировать работу алгоритма. Направления стрелок указывают, в какой последовательности ребра графа G попадают в стек ЕС.

Рисунок 8.24

Вначале в СТЕК помещается цикл 1 (V₀—V₁—V₂—V₃—V₄—V₀), он удаляется из графа, V₀ заносится в ЕС.

Затем из СТЕКА удаляется верхний элемент V₄. Все проходящие через него ребра удалены из графа, V₄ переносится в ЕС.

Затем в СТЕК помещается цикл 3, V₃ из СТЕКА переносится в ЕС.

Затем из СТЕКА в ЕС переносятся все элементы цикла 3, т.к. проходящие через них ребра удалены. Следующий верхний элемент — V₂ и т.д.

Оценим вычислительную сложность алгоритма.

Главный цикл 5 работает, пока СТЕК не пуст. Каждое ребро графа один раз записывается в СТЕК и один раз переносится в ЕС. Число итераций цикла 5 — О(m). Покажем что число шагов внутри каждой итерации ограничено константой. Одна итерация или записывает ребро в СТЕК, удаляя его из графа, или переносит в ЕС. Списки инцидентности ЗАПИСЬ[v] реализованы так, что для вершин u—v, соединенных ребром, вершина u в списке ЗАПИСЬ[v] содержит указатель на вершину v в списке ЗАПИСЬ[u] и наоборот. Это позволяет удалить ребро (v—u) за время, ограниченное константой. Построенный алгоритм является оптимальным, т.к. только выписывание эйлерова цикла потребует О(m) шагов.

Ответы

Ответ 1. Вначале обходим стороны пятиугольника, образуя цикл, затем «одним росчерком пера» пробегаем звездочку.