Дальнейшая оптимизация алгоритмов внешней сортировки

Время работы алгоритма внешней сортировки пропорционально . Здесь N — количество серий, k — количество вспомогательных лент, n — число элементов в файле.

Следовательно, первый путь ускорения работы алгоритма — увеличение числа вспомогательных лент. При этом сокращается количество операций переписи, но увеличивается количество сравнений из-за усложнения поиска минимума при слиянии и определения конца серии. Поэтому эффект достигается до определенного момента, а затем, при увеличении числа лент быстродействие алгоритма снижается.

Другой путь увеличения быстродействия — уменьшение числа серий. Для этого применяют комбинированные алгоритмы внешней и внутренней сортировок. Часть файла читается в буфер (массив) в оперативной памяти, где сортируется одним из быстрых методов. Затем данные переносятся на одну из вспомогательных лент, и процесс повторяется.

И, наконец, быстродействие алгоритма можно увеличить путем отказа от сбалансированности и однофазности. Проиллюстрируем этот метод на примере работы с тремя лентами (рисунок 4.12). В каждый момент элемента сливаются с двух лент на третью. Как только одна из входных лент окажется исчерпанной, она сразу становится выходной лентой для слияния с тех лент, которые еще не исчерпаны.

Рисунок 4.12

Для правильной работы алгоритма важно первоначальное распределение серий по лентам. Для этого применяется математический аппарат, основанный на рядах Фибоначчи.

Многофазная несбалансированная сортировка более эффективна, так как ликвидируется непроизводительная фаза разбиения, которая занимает половину всех операций переписи.

 

5 Рекурсивные алгоритмы

Рекурсивным называется объект, частично состоящий или определяющий сам себя. Мощность рекурсивного определения заключается в том, что оно позволяет с помощью конечного высказывания определить бесконечное множество объектов. Аналогично с помощью конечной рекурсивной программы можно описать бесконечное вычисление, причем программа не будет содержать явных повторений. Однако рекурсивные алгоритмы лучше всего использовать, если в решаемой задаче, вычисляемой функции или структуре обрабатываемых данных рекурсия уже присутствует явно. Например, функция факториал определяется следующим образом:

(а) 0! = 1;

(б) n > 0: n! = n * (n-1)!

В общем виде рекурсивную программу P можно выразить как некоторую композицию ρ из множества операторов S (не содержащих P) и самой P: P = ρ [S, P]. Если некоторая процедура P содержит явную ссылку на саму себя, то ее называют прямо рекурсивной, если же ссылается на другую процедуру Q, содержащую (прямую или косвенную) ссылку на P, то Р называют косвенно рекурсивной.

Подобно операторам цикла, рекурсивные процедуры могут приводить к незаканчивающимся вычислениям, и поэтому очевидно основное требование, чтобы рекурсивное обращение к P управлялось некоторым условием B, которое в какой-то момент становится ложным. Исходя из этого, более точно схему рекурсивных алгоритмов можно представить в любой из следующих форм:

1) P = IF B THEN ρ [S, P]

2) P = ρ [S, IF B THEN P]

Рекурсивные алгоритмы особенно подходят для задач, где обрабатываемые данные определяются в терминах рекурсии. Однако это не означает, что такое рекурсивное определение данных гарантирует бесспорность употребления для решения задачи рекурсивного алгоритма. Рекурсивные схемы естественны в ситуациях, где вычисляемые значения определяются с помощью простых рекуррентных отношений. Возьмем пример вычисления факториала. Первое из чисел определяется явно — f₀ = 1, а последующие определяются рекурсивным образом с помощью предшествующего числа: f_i+1=(i+1)*f_i. Соответствующая функция подсчета факториала выглядит следующим образом:

Function F(i:Integer):Integer;

Begin

If (I > 0) Then F:= i * F(i - 1) Else F:= 1

End;

Ясно, что в этом примере рекурсия может быть очень просто заменена итерацией:

i:= 0; F:= 1;

While (i < N) Do i:= i + 1; F:= i * F;

Однако существуют более сложные схемы рекурсий, которые необходимо переводить в итеративную форму. В качестве примера можно привести вычисление чисел Фибоначчи, определяемых рекурсивным соотношением fib_n+1=fib_n+fib_n-1 для n>0 и fib₁=1, fib₀=0. Прямое переписывание приводит к рекурсивной программе:

Function Fib(n:Integer):Integer;

Begin

If (n = 0) Then Fib:= 0

Else

If (n = 1) Then Fib:= 1

Else Fib:= Fib(n - 1) + Fib(n - 2)

End;

Вычисление fib_n путем обращения к Fib(n) приводит к рекурсивным активациям этой функции. Как часто это происходит? Каждое обращение с n>1 приводит еще к двум обращениям, т.е. общее число вызовов растет экспоненциально. При итеративном же решении этой задачи с помощью вспомогательных переменных x=fib_i и y=fib_i-1 удается избежать повторных вычислений одной и той же величины:

i:= 1; x:= 1; y:= 0;

While (i<n) Do

Begin

z:= x; x: = x + y; y:= z; i:= i+1

End;

Итак, следует избегать рекурсий там, где есть очевидное итерационное решение, что, впрочем, не означает, что от рекурсий следует избавляться любой ценой, так как существует множество задач, которые решаются много проще применением рекурсивных алгоритмов.

Одна из областей программирования — задачи так называемого «искусственного интеллекта». Здесь представлены алгоритмы, ищущие решения не по заданным правилам вычислений, а путем проб и ошибок. Обычно процесс проб и ошибок разделяется на отдельные задачи. Часто эти задачи наиболее естественно выражаются в терминах рекурсии и требуют исследования конечного числа подзадач. В общем виде весь процесс можно рассматривать как процесс поиска, строящий (и обрезающий) дерево подзадач. Во многих проблемах такое дерево поиска растет очень быстро, рост зависит от параметров задачи и часто бывает экспоненциальным. Соответственно увеличивается и стоимость поиска решения. Иногда, используя некоторые эвристики, дерево поиска удается сократить и тем самым свести затраты на вычисления к разумным пределам. Характерное свойство алгоритмов с возвратом заключается в том, что в них делаются шаги в направлении общего решения, но все они фиксируются (записываются) таким образом, что позже можно вернуться вспять, отбрасывая тем самым шаги, которые ведут не к общему решению, а заводят в тупик. Такой процесс называется возвратом или откатом (backtracking), а алгоритмы, реализующие описанную выше процедуру, называются алгоритмами с возвратом. Ниже приводится одна из абстрактных реализаций алгоритма с возвратом, в которой фиксированы глубина рекурсии n и максимальное число исследуемых путей m, что нередко применяется для решения задач такого типа.

Procedure Try(i: Integer);

Begin

k:= 0;

Repeat

k:= k + 1; {выбор k-го кандидата}

If <подходит> Then

Begin

<его запись>

If (i < n) Then

Begin

Try(i+1);

If <неудача> Then <стирание записи>

End

End

Until <удача> Or (k = m)

End;

Различными реализациями данной абстрактной схемы успешно решаются такие задачи, как, например, задача обхода конем шахматной доски, задача о восьми ферзях, задача о стабильных браках и задача оптимального выбора на примере задачи о рюкзаке.

6 Рекурсивные структуры данных

Рекурсивная структура данных включает в себя одну или более компонент, относящихся к тому же типу, что и сама структура.

Примеры.

1. Арифметическое выражение

Выражение состоит из терма, за которым следует знак операции, за которым опять идет терм. Сам терм — это либо переменная, обозначенная каким-либо идентификатором, либо заключенное в скобки выражение.

Type Expression = Record

Op: Operator;

t1, t2: Term

End;

Type Term = Record Case TermType: Boolean Of

True:(id: Alfa);

False:(SubExpression: Expression)

End;

2. Генеалогическое дерево.

Пусть генеалогическое дерево состоит из имени человека и двух генеалогических деревьев его родителей. Такое описание приводит к бесконечной структуре, хотя реально на определенном этапе информация о предках отсутствует. Получаем следующую структуру:

Type Node = Record Case Known: Boolean Of

True:(Name: Alfa; Father, Mother: Node);

False:({пусто})

End;

Из приведенных примеров видно, что для конечности описания рекурсивных данных, их конструкторы обязательно должны содержать условие для определения вариантов. В этом прослеживается аналогия между алгоритмами и данными. В приведенной форме способы описания данных в большинстве языков программирования отсутствуют. Для реализации динамических структур данных разработан специальный механизм динамического распределения памяти, т.е. механизм выделения памяти в тот момент, когда эти структуры появляются во время выполнения программы, а не при компиляции. В этом случае транслятор выделяет память для хранения адреса на компоненту, который называется указателем, или ссылкой. Эта структура имеет следующий вид:

	Сын
Мать				Отец

Возможность перемещения по указателю и выборочного изменения значения полей можно сравнить с оператором GOTO с той же опасностью ошибочного исхода. Как с помощью этого оператора можно строить любые программные схемы, так с помощью указателя можно строить любые сложные типы данных.

Односвязный линейный список

Наиболее простой способ объединить или связать некоторое множество элементов — это «вытянуть их в линию», организовать линейный список. В этом случае с каждым элементом нужно сопоставить лишь одну-единственную ссылку, указывающую на следующий элемент (ссылка P указывает на первый элемент списка):

P

NIL

Рисунок 6.1

Основные операции.

Пусть тип T описан следующим образом:

Type

PT = ^T;

T = Record

Key: Integer;

Next: PT;

End;

Var

n: Integer;

p, q, r: PT;

1. Процесс формирования списка.

Сформируем список из 3-х элементов с возрастанием ключей от 1 до 3, причем включение будем осуществлять в начало списка.

n:=3; p:=NIL;

While (n>0) Do

Begin

New(q);

q^.Key:=n;

q^.Next:=p;

p:=q;

n:=n-1

End;

2. Включение элемента по ссылке q после элемента списка, на который указывает ссылка p:

q^.Next:= p^.Next;

p^.Next=q;

3. Включение элемента с ключом k по ссылке q перед элементом списка, на который указывает ссылка p:

Новая компонента на самом деле включается после p^, но затем новая компонента и p^ «меняются» значениями:

new(q);

q^:=p^;

p^.Key:=k;

p^.Next:=q;

4. Удаление элемента, на который указывает p:

q:=p^.Next;

p^:=q^;

dispose(q);

5. Удаление элемента, следующего за элементом, на который указывает p:

r:=p^.Next;

p^.Next:=r^.Next;

dispose(r);

6. Проход по списку (применим операцию z(a:T) к каждому элементу списка):

q:=p;

While (q<>NIL) Do

Begin

z(q^);q:=q^.Next

End;

7. Поиск в списке элемента с заданным ключом x:

q:=p;

While (q<>NIL) And (q^.Key<>x) Do

q:=q^.Next;

If (q=NIL) Then WriteLn(‘В списке нет элемента со значением ’,x);

6.2 Двунаправленные и циклические списки

Самый простой способ соединить, или связать, множество элементов — это расположить их линейно в списке. В этом случае каждый элемент содержит только одну ссылку, связывающую его со следующим элементом списка.

Один из недостатков линейных списков: зная указатель на элемент списка, мы не имеем доступа к элементам ему предшествующим. Предположим, в списке сделали изменения. Ссылка последнего элемента теперь указывает на первый элемент списка (рисунок 6.2). Такой список называется циклическим.

Рисунок 6.2 — Циклический список

Таким образом, из любого элемента циклического списка можно достигнуть любого другого элемента данного списка. Циклический список не имеет первого и последнего элемента, следовательно, необходимо ввести такие элементы. Для этого заводят указатель на последний элемент списка, что автоматически делает следующий за ним первым.

Ни линейный список, ни циклический нельзя просмотреть в двух направлениях. Кроме этого, располагая только указателем на элемент, удалить его невозможно. Такого недостатка лишены двунаправленные (двусвязные) списки. Каждый элемент такого списка содержит 2 указателя; на следующий и на предыдущий.

Рисунок 6.3 — Двусвязный список

Мультисписки

Иногда желательно держать один и тот же элемент в нескольких списках, не повторяя его при этом в нескольких элементах. Например, если аналогом одномерного массива является линейный список, то аналогом многомерного массива будет мультисписок.

Каждый элемент мультисписка должен содержать столько указателей, в скольких списках он может участвовать.

Рисунок 6.4

Иногда, для ускорения поиска в каждом элементе мультисписка хранят его порядковый номер в списках, а в начальных массивах — количество элементов в данном подсписке. В результате, находясь на каком-то элементе, существует возможность выбрать более короткий список, в котором продолжить поиск.

Топологическая сортировка

Это процесс сортировки элементов, для которых определен частичный порядок, т.е. упорядочение задано не на всех, а на некоторых парах элементов.

Пример: в университетской программе одни предметы опираются на другие, поэтому одни предметы должны прослушиваться раньше, чем другие, т.е. сначала базовые, а затем те, которые основываются на базовых.

В общем виде частичный порядок на множестве S — это отношения между элементами этого множества, оно обозначается символом “<” — предшествует. Удовлетворяет следующим аксиомам:

1. для любых элементов: x, y, z из S, если x<y и y<z, то x<z — транзитивность.

2. если x<y, то не y<x — асимметричность.

3. не x<x — иррефлексивность.

Будем считать, что множество S, которое нужно топологически рассортировать является конечным, поэтому отношения частичного порядка можно проиллюстрировать с помощью графа (рисунок 6.5), в котором вершины обозначают элементы S, а ребра — отношения порядка.

Рисунок 6.5

Цель сортировки преобразовать частичный порядок в линейный (рисунок 6.6). Свойства 1 и 2 обеспечиваются отсутствием циклов. Это то необходимое условие, при котором преобразование возможно.

Рисунок 6.6

Рассмотрим необходимые структуры данных. Каждый элемент удобно представить тремя характеристиками: идентифицирующим ключом, множеством следующих за ним элементов и счетчиком предыдущих. Поскольку число последователей не задано a priori, то это множество удобно организовать в виде связанного списка. Аналогично множество последователей можно представить в виде списка.

type

lref = ^leader;

tref = ^trailer;

leader = record

key, count: integer;

trail: tref;

next: lref;

end;

trailer = record

id: lref;

next: tref;

end;

7 Древовидные структуры

Пусть древовидная структура определяется следующим образом: древовидная структура с базовым типом Т — это либо:

1. пустая структура; либо

2. узел типа Т, с которым связано конечное число древовидных структур с базовым типом Т, называемых поддеревьями.

Существует несколько способов изображения древовидной структуры. Например: вложенные множества, ломаная, граф (рисунок 7.1).

Упорядоченное дерево — это дерево, у которого ветви каждого узла упорядочены. Узел y, который находится непосредственно под узлом x, называется (непосредственным) потомком x; если x находится на уровне i, то говорят, что y — на уровне i + 1. Наоборот, узел x называется (непосредственным) предком y. Считается, что корень дерева расположен на уровне 1. Максимальный уровень какого-либо элемента дерева называется его глубиной или высотой.

Если элемент не имеет потомков, он называется терминальным элементом или листом, а элемент, не являющийся терминальным, называется внутренним узлом. Число (непосредственных) потомков внутреннего узла называется его степенью. Максимальная степень всех узлов есть степень дерева. Число ветвей, или ребер, которые нужно пройти, чтобы продвинуться от корня к узлу x, называется длиной пути к x. Корень имеет длину пути 1, его непосредственные потомки — длину пути 2 и т. д. Вообще, узел на уровне i имеет длину пути i. Длина пути дерева определяется как сумма длин путей всех его узлов. Она также называется длиной внутреннего пути. Например, длина внутреннего пути дерева, изображенного на рисунке 7.1, равна 52. Очевидно, что средняя длина пути есть , где — число узлов на уровне i.

Рисунок 7.1

Для того чтобы определить, что называется длиной внешнего пути, мы будем дополнять дерево специальным узлом каждый раз, когда в нем встречается нулевое поддерево (рисунок 7.2). При этом мы считаем, что все узлы должны иметь одну и ту же степень — степень дерева.

Рисунок 7.2

Длина внешнего пути теперь определяется как сумма длин путей всех специальных узлов. Если число специальных узлов на уровне i есть , то средняя длина внешнего пути равна . У дерева, приведенного на рисунке 7.2, длина внешнего пути равна 153.

Максимальное число узлов в дереве заданной высоты h достигается в случае, когда все узлы имеют d поддеревьев, кроме узлов уровня h, не имеющих ни одного. Тогда в дереве степени d первый уровень содержит 1 узел (корень), уровень 2 содержит d его потомков, уровень 3 содержит d² потомков d узлов уровня 2 и т. д. Это дает следующую величину:

Дерево идеально сбалансировано, если для каждого его узла количества узлов в левом и правом поддереве различаются не более чем на 1.

Пример: построение сбалансированного дерева

ProgramBildTree;

Type ref = ^node;

Node = record

Key: Integer;

Left, Right: ref;

End;

Var

n: Integer;

Root: ref;

Function tree(n: integer): ref;

Var

newnode: ref;

x, nl, nr: Integer;

Begin

If n = 0 then tree:= nil

Else

Begin

nl:= n div 2; nr:= n- nl –1;

Read(x); New (newnode);

With newnode^ do

Begin

key:=x; left:=tree(nl); right:=tree(nr);

End;

tree:= newnode;

End;

End;

Procedure PrintTree (t: ref; h: Integer);

Begin

If t <> nil Then

Begin

PrintTree(left,h+1);

For i:= 1 to h do Write (' ');

Writeln(Key);

PrintTree(right,h+1);

End;

End;

Begin

Read(n);

Root:= Tree(n);

PrintTree(root,0);

End.

Упорядоченные деревья степени 2 играют особо важную роль. Они называются бинарными деревьями. Упорядоченное бинарное дерево — конечное множество элементов (узлов), каждый из которых либо пуст, либо состоит из корня (узла), связанного с двумя различными бинарными деревьями, называемыми левым и правым поддеревом корня. Деревья, имеющие степень больше 2, называются сильно ветвящимися деревьями (multiway trees).

Бинарные деревья

Знакомыми примерами бинарных деревьев являются фамильное (генеалогическое) дерево с отцом и матерью человека в качестве его потомков, история теннисного турнира, где узлом является каждая игра, определяемая ее победителем, а поддеревьями — две предыдущие игры соперников; арифметическое выражение с двухместными операциями, где каждая операция представляет собой ветвящийся узел с операндами в качестве поддеревьев.

Теперь мы обратимся к проблеме представления деревьев. Ясно, что изображение таких рекурсивных структур с разветвлениями предполагает использование ссылок. Очевидно, что не имеет смысла описывать переменные с фиксированной древовидной структурой, вместо этого узлы определяются как переменные с фиксированной структурой, т. е. фиксированного типа, где степень дерева определяет число компонент-ссылок, указывающих на поддеревья данного узла. Ясно, что ссылка на пустое поддерево обозначается через nil.

type node = record

key: integer;

left, right: ^node;

end;

Рисунок 7.3 — Бинарное дерево

Обход дерева

Имеется много задач, которые можно выполнять на древовидной структуре; распространенная задача — выполнение заданной операции P с каждым элементом дерева. Здесь P рассматривается как параметр более общей задачи посещения всех узлов, или, как это обычно называют, обхода дерева.

Если рассматривать эту задачу как единый последовательный процесс, то отдельные узлы посещаются в некотором определенном порядке и могут считаться расположенными линейно. В самом деле, описание многих алгоритмов существенно упрощается, если можно говорить о переходе к следующему элементу дерева, имея в виду некоторое упорядочение.

Существуют три принципа упорядочения, которые естественно вытекают из структуры деревьев. Так же как и саму древовидную структуру, их удобно выразить с помощью рекурсии. Обозначив R — корень, а A и B — левое и правое поддеревья, мы можем определить такие три упорядочения:

1. Сверху вниз: R, A, B (посетить корень до поддеревьев).

2. Слева направо: А, R, В.

3. Снизу вверх: А, В, R (посетить корень после поддеревьев).

Теперь выразим эти три метода обхода как три конкретные программы с явным параметром t, означающим дерево, с которым они имеют дело, и неявным параметром Р, означающим операцию, которую нужно выполнить с каждым узлом.

Эти три метода легко сформулировать в виде рекурсивных процедур.

Procedure preorder (t: ref)

Begin

If t <> Nil Then

Begin

P(t);

preorder(t^.Left);

preorder(t^.Right);

End

End;

Procedure postorder (t: ref);

Begin

If t <> Nil Then

Begin

postorder(t^.Left);

postorder(t^.Right);

P(t);

End;

End;

Procedure inorder (t: ref);

Begin

If t <> Nil Then

Begin

inorder(t^.Left);

P(t);

inorder(t^.Right);

End;

End;

Пример подпрограммы, осуществляющей обход дерева, — это подпрограмма печати дерева с соответствующим сдвигом, выделяющим каждый уровень узлов.

Поиск элементов

Бинарные деревья часто используются для представления множеств данных, элементы которых ищутся по уникальному, только им присущему ключу. Если дерево организовано таким образом, что для каждого узла t[i] все ключи в левом поддереве меньше ключа t[i], а ключи в правом поддереве больше ключа t[i], то это дерево называется деревом поиска. В дереве поиска можно найти место каждого ключа, двигаясь, начиная от корня, и переходя на левое или правое поддерево каждого узла в зависимости от значения его ключа. Как мы видели, n элементов можно организовать в бинарное дерево с высотой не более чем log ₂ (n). Поэтому для поиска среди n элементов: может потребоваться не более log ₂ (n) сравнений, если дерево идеально сбалансировано. Очевидно, что дерево — намного более подходящая форма организации такого множества данных, чем линейный список.

Так как этот поиск проходит по единственному пути от корня к искомому узлу, его можно запрограммировать с помощью итерации:

Function Loc (x: integer; t: ref): ref;

Var

found: boolean;

Begin

found: = false;

While (t <> nil) and (Not found) do

Begin

if t^.key = x then found:= true

else

if t^.key > x then t:= t^.Left

else t:= t^.right

end;

Loc:= t;

End;

Функция Loc (x, t) имеет значение nil, если в дереве с корнем t не найдено ключа со значением x. Так же как в случае поиска по списку, сложность условия окончания цикла заставляет искать лучшее решение. При поиске по списку в конце его помещается барьер. Этот прием можно применить и в случае поиска по дереву. Использование ссылок позволяет связать все терминальные узлы дерева с одним и тем же барьером (рисунок 7.4). Полученная структура — это уже не просто дерево, а скорее, дерево, все листья которого прицеплены внизу к одному якорю.

Рисунок 7.4

Барьер можно также считать общим представлением всех внешних (специальных) узлов, которыми дополняется исходное дерево. Полученная в результате упрощенная процедура поиска описана ниже:

Function Loc(x: integer; t: ref): ref;

Begin

s^.key:= x; [барьер]

While t^.key <> x do

If x < t^,key Then t:= t^.left

Else t:= t^.right;

Loc:= t;

End;

Если в дереве с корнем t не найдено ключа со значением x, то в этом случае loc(x, t) принимает значение s, т. е. ссылки на барьер. Ссылка на s просто принимает на себя роль ссылки nil.

Включение элементов

Прежде всего, рассмотрим случай постоянно растущего, но никогда не убывающего дерева. Хорошим примером этого является задача построения частотного словаря. В этой задаче задана последовательность слов, и нужно установить число появлений каждого слова. Это означает, что, начиная с пустого дерева, каждое слово ищется в дереве. Если оно найдено, увеличивается его счётчик появлений, если нет — в дерево вставляется новое слово (с начальным значением счетчика, равным 1). Предполагаются следующий способ описания типов:

Type

ref = ^Words;

Words = record

Key: Integer;

Count: Integer;

Left, Right: ref;

End;

Считая, кроме того, что у нас есть исходный файл ключей F, а переменная root указывает на корень дерева поиска, мы можем записать программу следующим образом:

Reset(f);

While Not EOF(f) do Begin

Read(f,k); Search(x, root);

End;

Определение пути поиска здесь вновь очевидно. Но если он приводит в «тупик», т.е. к пустому поддереву, обозначенному ссылочным значением nil, то данное слово нужно вставить в дерево на место пустого поддерева.

Процесс поиска представлен в виде рекурсивной процедуры. Использование барьера вновь упрощает задачу.

Procedure Search (x: integer; Var p: ref);

Begin

s^.key:= x;

If x < p^.key Then Search(x,p^.Left) Else

If x > p^.key Then Search(x,p^.Right) Else

If p <> s Then p^.Count:= p^.Count + 1 Else

Begin

{ включение }

New(p);

With p^ do

Begin

Key:= x; Left:= s;

Right:= s; Count:=1;

End;

End;

End;

Удаление из дерева

Теперь мы переходим к задаче, обратной включению, а именно удалению. Нам нужно построить алгоритм для удаления узла с ключом x из дерева с упорядоченными ключами. К сожалению, удаление элемента обычно не так просто, как включение. Оно просто в случае, когда удаляемый элемент является терминальным узлом или имеет одного потомка.

Трудность заключается в удалении элементов с двумя потомками, поскольку мы не можем указывать одной ссылкой на два направления. В этом случае удаляемый элемент нужно заменить либо на самый правый элемент его левого поддерева, либо на самый левый элемент его правого поддерева. Ясно, что такие элементы не могут иметь более одного потомка. Различают три случая:

1. Компоненты с ключом, равным x, нет.

2. Компонента с ключом x имеет не более одного потомка.

3. Компонента с ключом x имеет двух потомков.

Легко удалить терминальный узел, или узел, имеющий одного потомка. В случае двух потомков удаляемый элемент нужно заменить либо на самый правый элемент его левого поддерева, либо на самый левый элемент его правого поддерева. Ясно, что такие элементы не могут иметь более 1-го потомка.

Procedure Delete (x: integer; var p: ref);

Var

q: ref;

Procedure del (var r: ref);

Begin

If r^.right <> nil Then del(r^.right)

Else

Begin

q^.key:= r^.key;

q:= r; r:= r^.left

End

End;

Begin { delete }

If p = nil Then Writein ('word is not in tree')

Else If x < p^.key Then delete(x, p^.left)

Else If x > p^.key Then delete(x, p^.right)

Else

Begin { delete p^ }

q:= p;

If q^.right = nil Then p:= q^.left

Else If q^.left = nil

Then p:= q^.right

Else del(q^.left);

Dispose(q)

End

End; [ delete }

Вспомогательная рекурсивная процедура del вызывается только в 3-м случае. Она «спускается» вдоль самой правой ветви левого поддерева удаляемого узла q^ и затем заменяет существенную информацию (ключ и счетчик) в q^ соответствующими значениями самой правой компоненты r^ этого левого поддерева, после чего от r^ можно освободиться.

АВЛ-деревья

Анализ задачи поиска по дереву с включениями узлов показывает, что эффективность алгоритма зависит от формы, которую принимает растущее дерево. Легко найти наихудший случай: ключи поступают в порядке возрастания, и дерево оказывается полностью вырожденным, то есть превращается в линейный список. В этом случае среднее число сравнений ключей равно N/2. Наилучший вариант получается, если дерево строится идеально сбалансированным, в этом случае среднее число сравнения равно log₂N.
Н. Вирт показал, что строя идеально сбалансированное дерево, следует ожидать выигрыш в длине пути поиска в среднем не более 39%. Эта цифра достаточно низка, и в большинстве случаев не оправдывает затрат на восстановление идеальной сбалансированности дерева.

Попробуем добиться эффективности менее дорогим способом, введя менее строгое понятие сбалансированности дерева. Критерий сбалансированности дерева (Адельсон-Вельский, Ландис, 1962): Дерево является сбалансированным тогда и только тогда, когда для каждого его узла высота его двух поддеревьев различается не более чем на 1.

Дерево, удовлетворяющее этому критерию, называют АВЛ-деревом (по имени авторов) или сбалансированным деревом. Понятно, что идеально сбалансированное дерево является АВЛ-деревом.

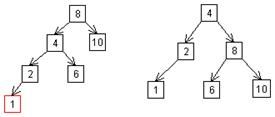
Рисунок 7.5 — АВЛ-дерево

Рассмотрим включение элемента в сбалансированное дерево.

Возможны 3 случая:

1. hL = hR: L и R становятся неравной высоты, но критерий сбалансированности не нарушается

2. hL < hR: L и R приобретают равную высоту, т.е. сбалансированность даже улучшается

3. hL > hR: критерий сбалансированности нарушается, и дерево нужно трансформировать, такая перестройка называется поворотом.

Рассмотрим третий случай. Включение узлов 1, 3, 5 или 7 требует последующей балансировки. Можно обнаружить, что имеется лишь две существенно различные ситуации, требующие индивидуального подхода. Оставшиеся могут быть получены симметричными преобразованиями этих двух.

Случай 1. Включение ключа 1 или 3. Для балансировки выполняется так называемый левый поворот.

Рисунок 7.6

Случай 2. Включение узла 5 или 7. Теперь для балансировки выполняется два поворота — левый и правый.

Рисунок 7.7

Сильно ветвящиеся деревья

До сих пор мы ограничивали наши рассуждения деревьями, в которых каждый узел имеет самое большее двух потомков, т.е. бинарными деревьями. Этого вполне достаточно, если, например, мы хотим представить родственные отношения с предпочтением «восходящей линии», т. е. когда для каждого человека указываются его родители. В конце концов, ни у кого не бывает более двух родителей. Но как быть тому, кто предпочитает изображать «нисходящую линию»? Ему придется столкнуться с тем фактом, что некоторые люди имеют более двух детей, поэтому его деревья будут содержать узлы со многими ветвями.

Если, например, задана абсолютная верхняя граница количества детей, то можно представить детей в виде компоненты-массива в записи, представляющей человека. Но если число детей у разных людей сильно варьируется, то это может привести к неэкономному расходу памяти. В этом случае намного правильнее расположить потомство в виде линейного списка со ссылкой в записи родителей на самого младшего (или самого старшего) отпрыска. Возможное описание типа для такого случая:

Type

person =Record

Name: string;

Sibling: ^person;

offspring: ^person

End;

Имеется очень важная область применения сильно ветвящихся деревьев, которая представляет общий интерес. Это — формирование и использование крупномасштабных деревьев поиска, в которых необходимы и включения, и удаления, но для которых оперативная память недостаточно велика или слишком дорогостояща, чтобы использовать ее для долговременного хранения.

Рисунок 7.8

Предположим, что узлы дерева должны храниться на внешнем запоминающем устройстве, таком, как диск. Принципиально новое — это лишь то, что ссылки представляют собой адреса на диске, а не адреса оперативной памяти. Если множество данных, состоящее, например, из миллиона элементов, хранится в виде бинарного дерева, то для поиска элемента потребуется в среднем около шагов поиска. Поскольку теперь каждый шаг включает обращение к диску, будет весьма желательна организация памяти, требующая меньше обращений. Сильно ветвящееся дерево является идеальным решением этой проблемы. Если происходит обращение к некоторому одиночному элементу, расположенному на внешнем устройстве, то без больших дополнительных затрат можно обращаться также к целой группе элементов. Отсюда следует, что дерево нужно разделить на поддеревья, считая, что все эти поддеревья одновременно полностью доступны. Такие поддеревья называют страницами. На рисунке 7.8 показано бинарное дерево, разделенное на страницы, состоящие из 7 узлов каждая.

Уменьшение количества обращений к диску — а теперь обращение к каждой странице предполагает обращение к диску — может быть значительным. Предположим, что мы решили помещать на странице 100 узлов (это разумная цифра), тогда дерево поиска, содержащее миллион элементов, потребует в среднем только обращений к страницам вместо 20. Но конечно, если дерево растет «случайным образом», то наихудший случай может потребовать даже 10⁴ обращений! Понятно, что в случае сильно ветвящихся деревьев почти обязательна схема управления их ростом.

B–деревья

При поиске критерия управляемого роста необходимо отвергнуть идеальную сбалансированность, т.к. она требует слишком больших затрат. Разумный критерий был сформулирован Р. Бэйром: каждая страница (кроме одной) содержит от n до 2n узлов при заданном постоянном n. Следовательно, в дереве с N элементами и максимальным размером страницы 2n узлов наихудший случай потребует обращений к страницам. Кроме того, коэффициент использования памяти составляет не хуже 50%. Рассматриваемые структуры данных называются B–деревьями и имеют следующие свойства:

1. Каждая страница содержит не более 2n элементов.

2. Каждая страница, кроме корневой, содержит не менее n элементов.

3. Каждая страница является либо листом, т.е. не имеет потомков, либо имеет m + 1 потомков, где m — число находящихся на ней ключей.

4. Все листья находятся на одном и том же уровне.

Сформулируем описание страницы (рисунок 7.9).

Рисунок 7.9

const

nn = 2*n;

type

item = record

key: integer;

p: ref;

………………..

end;

ref = ^page;

page = record

m: index;

p0: ref;

e: array[1..nn] of item;

end;

На рисунке 7.10 показано Б-дерево порядка 2 с 3 уровнями. Все страницы содержат 2, 3 или 4 элемента. Исключением является корень, которому разрешается содержать только один элемент. Все листья находятся на уровне 3. Ключи расположены в возрастающем порядке слева направо, если спроектировать дерево на один уровень, вставляя потомков между ключами, находящимися на странице-предке. Такое расположение представляет естественное развитие принципа организации бинарных деревьев поиска и определяет метод поиска элемента с заданным ключом. Рассмотрим страницу, имеющую вид, как показано на рисунке 7.9, и пусть задан аргумент поиска х. Предполагая, что страница считана в оперативную память, мы можем использовать известные методы поиска среди ключей k₁,..., k_m. Если т достаточно велико, можно применить бинарный поиск, если оно сравнительно небольшое, подойдет простой последовательный поиск. (Заметим, что время, требующееся для поиска в оперативной памяти, вероятно, пренебрежимо мало по сравнению со временем, ко