
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кратчайшие пути с фиксированными платежамиСодержание книги Поиск на нашем сайте
Все задачи о нахождении кратчайшего пути между двумя фиксированными вершинами исходили из следующего предположения: если кратчайший путь от s до t проходит через вершину k, то его отрезок от s до k будет кратчайшим путем от s до k и отрезок от k до t будет кратчайшим путем от k до t. Существует класс задач, для которых это не так. Это задачи с фиксированными платежами. Подобные задачи возникают в том случае, если за прохождение вершины сети взимается плата. Решаются такие задачи довольно сложно, но есть один класс транспортных задач, которые сводятся к уже рассмотренным нами задачам. ШТРАФЫ ЗА ПОВОРОТЫ Имеется сеть улиц с односторонним или двусторонним движением. Рассмотрим вначале случай одностороннего движения. При выполнении поворота вводится некая фиксированная плата — задержка или штраф. Этот штраф зависит от направления движения при въезде и выезде. За выполнение запрещенного поворота взимается бесконечно большой штраф.
Рисунок 8.35 Неотрицательные числа, приписанные дугам, представляют плату или время проезда. Кроме того, предполагается, что за выполнение каждого поворота взимается штраф, равный 3. Требуется определить минимальный путь из 1 в 8. Теорема В сети со штрафами за повороты кратчайший путь из s в t, проходящий через k, не обязан содержать кратчайшие пути от s до k и от k до t. Пример. (рисунок 35) 1-2-3-4-8 — кратчайший путь со стоимостью 15. 1-2-3-4 — путь со стоимостью 11. 1-2-6-5-4 — кратчайший путь со стоимостью 10. Мы уже умеем находить кратчайшие пути в задачах, где стоимости приписаны только дугам. Следовательно, по исходной сети нужно построить новую фиктивную сеть, где бы штрафы за повороты включились бы в стоимость дуг. Затем в фиктивной сети найти кратчайший путь и по нему восстановить кратчайший путь в исходной сети. АЛГОРИТМ ПОИСКА КРАТЧАЙШЕГО ПУТИ В СЕТИ СО ШТРАФАМИ ЗА ПОВОРОТЫ Шаг 1. Ввести фиктивный источник s0 и соединить его дугой с источником s. Ввести фиктивный сток t0 и соединить его дугой со стоком t. Стоимости фиктивных дуг положить равными 0 и считать, что повороты из фиктивных вершин никогда не выполняются. Шаг 2. Каждой i-й дуге расширенной сети, полученной на шаге 1, приписать имя Li. Если исходная сеть содержала m дуг, то дугам будут приписаны имена L0,L1,…,Lm+1 (рисунок 8.36).
Рисунок 8.36 Шаг 3. Построение фиктивной сети (рисунок 8.37). Каждой дуге расширенной сети будет соответствовать вершина фиктивной. Две вершины фиктивной сети Li и Lj соединены дугой только в том случае, если в исходной сети конец дуги Li был бы началом дуги Lj. Стоимость такой дуги определяется по следующей формуле:
Рисунок 8.37 Стоимости дуг фиктивной сети:
?Вопрос 1. Почему стоимость дуги L5→L10 равна 3, а не 6 (стоимость дуги + штраф за поворот)? Шаг 4. Используя алгоритм Дейкстры, определить в фиктивной сети кратчайший путь. Шаг 5. По кратчайшему пути в фиктивной сети восстановить путь в исходной: Останов. Возникает вопрос, каким образом, зная две дуги, определить плату за поворот. В нашей задаче улицы имеют только два направления: горизонтальное и вертикальное. Будем хранить информацию о направлении каждой дуги в двумерном массиве BIN. Если BIN[i,j]=0, то дуга i→j имеет горизонтальное направление, если 1, то вертикальное. Рассмотрим сумму BIN[i,j]+BIN[j,k], производя сложение по mod 2. Если поворот происходит, то эта сумма равна 0+1 или 1+0, т.е. 1. Если поворот не происходит, то эта сумма равна 0+0 или 1+1, т.е. 0. ?Вопрос 2. Как хранить информацию о поворотах в случае двустороннего движения? Подсчитаем вычислительную сложность алгоритма. Построение фиктивной сети можно выполнить за O(n2) шагов. Если соответствие дуг исходной сети вершинам фиктивной записать в специальный массив размерности 2x(m+2), то восстановление пути пропорционально его длине, т.е. O(n). Алгоритм Дейкстры — O(n2). Окончательно, вычислительная сложность равна O(n2). Ответы Ответ 1. В фиктивную вершину поворот не производится. Ответ 2. Кодировать возможные направления числами: 0,1,2,3. Первые K кратчайших путей При решении практических задач часто бывает недостаточно знать один самый короткий путь. Будем искать первые K кратчайших путей между парой фиксированных вершин s и t, расположенных в порядке возрастания длин и не содержащих контуров. Граф, как обычно, не должен содержать контуры отрицательного веса. ?Вопрос 1. В каком случае первые K кратчайших путей могут быть найдены уже рассмотренными нами методами? Основная идея алгоритма — поиск отклонений от уже найденных кратчайших путей. Пусть мы уже нашли первые j путей (j<K). Обозначим их P1, P2,…, Pj. Найдем j+1 кратчайший путь. Рассмотрим последний найденный путь Pj=s, Зафиксируем какую-нибудь вершину этого пути, не равную t. Пусть это будет i-тая вершина
Рисунок 8.38 Запреты нужны для того, чтобы, во-первых, не сгенерировать путь, содержащий цикл; во-вторых, не сгенерировать уже найденный путь. Для этого: 1. Запретим использовать вершины s, 2. Сравним все уже найденные пути P1, P2,…, Pj-1 с путем Pj. Выберем из них те, у которых начальный участок из i вершин s, С учетом этих запретов можно найти отклонение Уже найденные кратчайшие пути будем хранить в окончательном списке L0, отклонения от кратчайших путей — в рабочем списке L. Поместим в L отклонения от кратчайшего пути Pj во всех вершинах. Минимальный путь из списка L переместим в список L0. Этот путь и будет j+1-м кратчайшим путем. АЛГОРИТМ ЙЕНА ПОИСКА ПЕРВЫХ K КРАТЧАЙШИХ ПУТЕЙ БЕЗ КОНТУРОВ Шаг 1. Положить j=1. С помощью алгоритма Форда-Беллмана или Дейкстры найти кратчайший путь от s до t и поместить его в L0. Шаг 2. Для всех вершин Шаг 3. Наложить запрет на использование вершин s, Шаг 4. С помощью алгоритма Форда-Беллмана или Дейкстры найти кратчайший путь от Полученный путь поместить в список L. Шаг 5. Восстановить матрицу весов A и допустимость вершин s, Положить i=i+1. Если Шаг 6. Все отклонения от j-го пути уже помещены в список L. Положить j=j+1. Если L пуст, то останов; иначе найти в L минимальный путь и перенести его в список L0. Если j=K, то останов; иначе переход к шагу 2. Подсчитаем вычислительную сложность алгоритма Йена и оценим размерность рабочих списков L0 и L. Для каждого из первых K-1 путей ищем отклонения во всех вершинах. Вершин в пути не более n, поиск отклонения для одной вершины O(n3) или O(n2). Окончательно, вычислительная сложность равна O(K*n4) или O(K*n3) для неотрицательных весов. Длина каждого пути не превосходит n (пути не содержат циклов). Количество путей в списке L0 не превосходит K; количество путей в списке L не превосходит числа отклонений (во всех вершинах, кроме последней) для K-1 пути, т.е. (K-1)*(n-1). Пути можно хранить в виде массивов, но наиболее экономным способом является динамическая структура «связанный список» для пути и «списки инцидентности» для списков L0 и L. Ответы Ответ 1. Если в графе имеется не менее K различных путей одной и той же минимальной длины. ПРИЛОЖЕНИЕ 1. Данный список NP-полных задач, хоть и не претендует на полноту, но может дать некоторое представление о подобных задачах, возникающих в различных областях математики и информатики. Каждая из таких задач допускает две возможных постановки: 1) задача оптимизации; 2) задача распознавания. В качестве примера рассмотрим задачу о КОММИВОЯЖЕРЕ. Оптимизационная постановка выглядит так: УСЛОВИЕ. Заданы конечное множество C городов, целые положительные расстояния d(c1,c2) для каждой пары городов c1, c2. ВОПРОС ОПТИМИЗАЦИИ. Найти маршрут минимальной длины, проходящий через все города и возвращающийся в исходный пункт. Чтобы получить теперь задачу распознавания, введем дополнительный параметр — числовую границу B. ВОПРОС РАСПОЗНАВАНИЯ. Существует ли маршрут, проходящий через все города, длина которого не превосходит B, где B — целое положительное число? (Если решается задача на максимум, то условие «не превосходит B» заменяется условием «не меньше B».) Традиционно к NP-полным задачам относятся задачи распознавания, однако соответствующие им задачи оптимизации эквивалентны им по сложности, поэтому при формулировке задач будем использовать любую постановку. 1. РАСКРАШИВАЕМОСТЬ ГРАФА (ХРОМАТИЧЕСКОЕ ЧИСЛО) УСЛОВИЕ. Заданы граф G=<V,E> и положительное целое число K |V|,где |V| — число вершин графа. ВОПРОС. Верно ли, что граф K — раскрашиваем? (Граф называется K–раскрашиваемым, если его вершины можно раскрасить в K цветов так, чтобы любые две соседние вершины были раскрашены в различные цвета). 2. КЛИКА УСЛОВИЕ. Заданы граф G=<V,E> и положительное целое число K |V|. ВОПРОС. Верно ли, что граф G содержит клику размера не менее K? (Существует ли подграф графа G такой, что число вершин в нем K и любые две вершины соединены ребром?) 3. ВЕРШИННОЕ ПОКРЫТИЕ УСЛОВИЕ. Заданы граф G=<V,E> и положительное целое число K |V|. ВОПРОС. Имеется ли в графе вершинное покрытие не более чем из K элементов? (Имеется ли такое подмножество вершин V' V мощности не более K, что для любого ребра (u-v) Є V хотя бы одна из вершин u, v принадлежит V'?) 4. РАЗБИЕНИЕ УСЛОВИЕ. Заданы конечное множество A и положительный целый вес w(a) для каждого a Є A. ВОПРОС. Существует ли подмножество A' A такое, что суммарный вес элементов, принадлежащих A', равен суммарному весу элементов, не принадлежащих A'? (Иными словами, можно ли A разбить на два подмножества, равные по весу?) 5. РЮКЗАК УСЛОВИЕ. Задано конечное множество A, положительные целые веса w(a), стоимости s(a) для каждого a Є A и общее ограничение на вес K. ВОПРОС. Найти из всевозможных выборок A' A такую, чтобы суммарный вес входящих в него элементов не превосходил K, а суммарная стоимость была максимальна. 6. РЮКЗАК С КРАТНЫМ ВЫБОРОМ ЭЛЕМЕНТОВ УСЛОВИЕ. Задано конечное множество A, положительные целые веса w(a), стоимости s(a) для каждого a Є A, общее ограничение на вес K и минимальная стоимость B. ВОПРОС. Можно ли так сопоставить каждому элементу a Є A целое число c(a) (кратность), чтобы суммарный вес всех предметов из A с учетом кратностей не превосходил K, а суммарная стоимость тех же предметов была не меньше B? 7. УПАКОВКА В КОНТЕЙНЕРЫ УСЛОВИЕ. Заданы конечное множество A и размеры s(a) Є [0, 1] каждого предмета. ВОПРОС. Найти такое разбиение множества A на непересекающиеся A1, A2, …, Ak, чтобы сумма размеров предметов в каждом Ai не превосходила 1, и k было минимальным. 8. ДИНАМИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ ПАМЯТИ УСЛОВИЕ. Заданы множество элементов данных A, целые положительные s(a) — размер каждого элемента, r(a) — время его поступления, d(a) — время его жизни, положительное целое число D — размер области памяти. ВОПРОС. Существует ли для множества данных A допустимое распределение памяти? Иными словами, существует ли такая функция: A ® {1, 2, …, D}, что для каждого элемента a Є A интервал ((a), (a) + s(a) — 1) — место, занимаемое им в динамической памяти, содержался бы в [1,D] и в любой фиксированный момент времени t0 интервалы для данных с 9. МНОЖЕСТВО ПРЕДСТАВИТЕЛЕЙ УСЛОВИЕ. Задано семейство C подмножеств множества S, положительное целое число K. ВОПРОС. Содержит ли S множество представителей для C, т.е. существует ли в S подмножество S' мощности не более K такое, что S' содержит, по крайней мере, один элемент из каждого множества семейства C. 10. УПОРЯДОЧЕНИЕ ВНУТРИ ИНТЕРВАЛОВ УСЛОВИЕ. Задано конечное множество заданий T и для каждого задания t Є T целое число r(t) 0 — время готовности, целые положительные d(t) и l(t) — директивный срок и длительность. ВОПРОС. Существует ли для T допустимое расписание, т.е. функция: T ® N (N — множество натуральных чисел), сопоставляющая заданию t момент начала его выполнения (t)? (Иными словами, задание t выполняется с момента времени (t) до (t) + l(t), оно не может быть начато ранее момента r(t), должно быть закончено не позднее d(t), и временной интервал выполнения одного задания не может перекрываться с интервалом другого). 11. СОСТАВЛЕНИЕ УЧЕБНОГО РАСПИСАНИЯ УСЛОВИЕ. Заданы множество H рабочих часов, множество C преподавателей, множество T учебных дисциплин, для каждого преподавателя c дано подмножество A(c) из H, называемое «допустимыми часами преподавателя c», для каждой дисциплины t подмножество A(t) множества H, называемое «допустимыми часами дисциплины t», и для каждой пары (c,t) Є C T целое положительное число R(c,t), называемое «требуемой нагрузкой». ВОПРОС. Существует ли учебное расписание, обслуживающее все дисциплины? Иными словами, существует ли функция f: CT´H ® {0,1} (где f(c,t,h)=1 означает, что преподаватель c занимается дисциплиной t в момент h), удовлетворяющая следующим условиям: (1) f(c,t,h)=1 только тогда, когда h Є пересечению A(c) и A(t); (2) для каждого h Є H и c Є C существует не более одного t Є T такого, что f(c,t,h)=1; (3) для каждого h Є H и t Є T существует не более одного c Є C такого, что f(c, t, h)=1; (4) для каждой пары (c,t) Є CT существует ровно R(c,t) значений h, для которых f(c,t,h)=1. 12. МИНИМАЛЬНОЕ ПОКРЫТИЕ УСЛОВИЕ. Задано семейство C подмножеств конечного множества S и положительное целое число K |C|. ВОПРОС. Существует ли покрытие C' из C мощности не более K? Иными словами, существует ли в C такое подмножество C', что любой элемент из S принадлежит, по крайней мере, одному подмножеству из C'? 13. МИНИМАЛЬНЫЙ НАБОР ТЕСТОВ УСЛОВИЕ. Задано конечное множество A возможных диагнозов, набор C подмножеств множества A, представляющий тесты, и положительное целое число J |C|. ВОПРОС. Существует ли в C поднабор C', мощности не более J, такой, что для любой пары Ai, Aj возможных диагнозов имеется некоторый тест c Є C', содержащий ровно один из них? 14. САМЫЙ ДЛИННЫЙ ПУТЬ УСЛОВИЕ. Заданы граф G=<V,E>, целые положительные длины l(e) для всех ребер, выделенные вершины s и t и положительное целое число B. ВОПРОС. Существует ли в G элементарный путь из s в t, имеющий длину не менее B? 15. НЕЗАВИСИМОЕ МНОЖЕСТВО УСЛОВИЕ. Заданы граф G=<V, E> и положительное целое число K |V|. ВОПРОС. Существует ли в V независимое множество мощности не менее K? Иными словами, верно ли, что существует подмножество V' Є V такое, что |V'|<=K и никакие две вершины из V' не соединены ребром из E? 16. КУБИЧЕСКИЙ ПОДГРАФ УСЛОВИЕ. Задан граф G=<V,E>. ВОПРОС. Существует ли в E непустое подмножество E' такое, что в графе G'=<V,E'> любая вершина имеет степень, равную 3 или 0? 17. МИНИМАЛЬНЫЙ РАЗРЕЗ УСЛОВИЕ. Заданы граф G=<V,E>, вес w(e) каждого ребра e Є E и положительное целое число K. ВОПРОС. Существует ли разбиение множества V на два таких непересекающихся множества V1 и V2, что сумма весов ребер из E, соединяющих вершины из множеств V1 и V2, не превосходит K? 18. МИНИМАЛЬНЫЙ РАЗРЕЗ С ОГРАНИЧЕНИЯМИ УСЛОВИЕ. Заданы граф G=<V,E> с двумя выделенными вершинами s и t, вес w(e) каждого ребра e Є E и положительные целые числа B и K (B |V|). ВОПРОС. Существует ли разбиение множества V на два таких непересекающихся множества V1 и V2, что s Є V1, t Є V2, |V1| B, |V2| B и сумма весов ребер из E, соединяющих вершины из множеств V1 и V2, не превосходит K? 19. НАДЕЖНОСТЬ СЕТИ УСЛОВИЕ. Заданы граф G=<V,E>, подмножество V' Є V, для каждого e Є E рациональное число p(e), 0 p(e) 1 — вероятность неисправности, положительное рациональное число q 1. ВОПРОС. Верно ли, что с вероятностью, не меньшей q, любые две вершины из V соединены хотя бы одним путем, не содержащим неисправных ребер? 20. КРАТЧАЙШИЙ ПУТЬ С ОГРАНИЧЕНИЯМИ ПО ВЕСУ УСЛОВИЕ. Заданы граф G=<V,E> с двумя выделенными вершинами s и t, целые положительные веса w(e) и длина l(e) каждого ребра e Є E и положительные целые числа B и K. ВОПРОС. Существует ли в G элементарный путь из s в t, веса не более B и длины не более K? 21. СЕЛЬСКИЙ ПОЧТАЛЬОН УСЛОВИЕ. Заданы граф G=<V,E> целая положительная длина l(e) каждого ребра e Є E, E' — подмножество E и положительное целое число K. ВОПРОС. Существует ли в G цикл, включающий каждое ребро из E' и имеющий длину не более K? 22. МИНИМАЛЬНОЕ ПО МОЩНОСТИ МАКСИМАЛЬНОЕ ПАРОСОЧЕТАНИЕ УСЛОВИЕ. Заданы граф G=<V,E> и положительное целое число K |E|. ВОПРОС. Существует ли в E непустое подмножество E' такое, что |E'| K и E'- максимальное паросочетание, т.е. никакие два ребра из E' не имеют общего конца, а любое ребро из множества E \ E' имеет общий конец с одним из ребер множества E'? 23. СУММА ВЕСОВ УСЛОВИЕ. Задано конечное множество A, положительные целые веса w(a) для каждого a Є A и положительный целый вес K. ВОПРОС. Существует ли такое подмножество A' множества A, что сумма весов его элементов равна K? 24. ДОСТАТОЧНОСТЬ ЧИСЛА РЕГИСТРОВ ДЛЯ РЕАЛИЗАЦИИ ЦИКЛОВ УСЛОВИЕ. Заданы множество A параметров цикла; целое положительное число N — длина цикла; для каждого параметра a (1) начальное время t(a) — целое, неотрицательное; (2) целая положительная продолжительность d(a); (3) целое положительное число K. ВОПРОС. Достаточно ли K регистров для запоминания параметров цикла? Иными словами, существует ли такое назначение регистров: A ® {1, 2, …, K}, что если (a1) = (a2) для некоторых a1, a2 Є A, то из неравенства t(a1) t(a2) следует, что t(a1)+d(a1) t(a2) и t(a2)+d(a2) (mod N) t(a1)? 25. РАЗБИЕНИЕ НА КЛИКИ УСЛОВИЕ. Заданы граф G=<V,E> и положительное целое число K≤|V|. ВОПРОС. Можно ли разбить вершины графа G на k≤K непересекающихся множеств V1,V2,…,Vk таких, что для всех i (1≤i≤k) подграф, индуцированный множеством Vi, был бы полным? 26. РАСЩЕПЛЕНИЕ МНОЖЕСТВА УСЛОВИЕ. Задан набор C подмножеств множества S. ВОПРОС. Существует ли такое разбиение множества S на два подмножества, что ни одно подмножество из C не содержится целиком ни в S1, ни в S2? 27. КРАТЧАЙШАЯ ОБЩАЯ НАДПОСЛЕДОВАТЕЛЬНОСТЬ УСЛОВИЕ. Заданы конечный алфавит A, конечное множество R слов в алфавите A и положительное целое число K. ВОПРОС. Существует ли такое слово wЄA*, что |w|≤K и каждое слово xЄR есть подпоследовательность слова w (т.е. w=w0x1w1x2w2…xkwk,, где wi ЄA*, а x=x1, x2,…, xk)? 28. МАКСИМАЛЬНОЕ ЧИСЛО ОГРАНИЧЕННЫХ НЕПЕРЕСЕКАЮЩИХСЯ ПУТЕЙ УСЛОВИЕ. Задан граф G<V,E> с выделенными вершинами s и t и заданы положительные целые числа B и K(B,K≤|V|). ВОПРОС. Верно ли что в G содержится не менее B путей из s в t, попарно не имеющих общих вершин и включающих не более K ребер? 29. КАРКАС ОГРАНИЧЕННОЙ СТЕПЕНИ УСЛОВИЕ. Заданы граф G=<V,E> и положительное целое число K≤|V|. ВОПРОС. Существует ли в графе G каркас, у которого степени всех вершин не превосходят K? 30. КАРКАС С МАКСИМАЛЬНЫМ ЧИСЛОМ ЛИСТОВ УСЛОВИЕ. Заданы граф G=<V,E> и положительное целое число K≤|V|. ВОПРОС. Существует ли в графе G каркас, у которого не менее K вершин степени 1? 31. ДЕРЕВО ШТЕЙНЕРА УСЛОВИЕ. Заданы граф G=<V,E>, положительный целый вес w(e) каждого ребра eЄE, подмножество R вершин графа и положительное целое число B. ВОПРОС. Существует ли в графе G дерево, содержащее все вершины из R, что сумма весов ребер этого поддерева не превосходит B? 32. K КРАТЧАЙШИХ ПУТЕЙ УСЛОВИЕ. Задан граф G<V,E> с выделенными вершинами s и t, положительный целый вес w(e) каждого ребра eЄE и заданы положительные целые числа B и K. ВОПРОС. Верно ли, что в G содержится B различных путей из s в t, длины которых не превосходят K? P.S. Любая из этих задача при n20 эффективно решается алгоритмом с возвратом. библиографический список 1. Липский В. Комбинаторика для программистов. М.: Мир, 1988. 2. Алкок Д. Язык Паскаль в иллюстрациях. М.: Мир, 1988. 3. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженеров. М.: Энергоатомиздат, 1988. 4. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М.: Мир, 1982. 5. Филлипс Д., Гарсиа-Диас А. Методы анализа сетей. М.: Мир, 1984. 6. Кристофидес Н. Теория графов. Алгоритмический подход. М.: Мир, 1978. 7. Лорьер Ж.Л. Системы искусственного интеллекта. М.: Мир, 1991. 8. Вирт Н. Алгоритмы + структуры данных = программы. М.: Мир,1985. 9. Нагао М., Катаяма Т., Уэмура С. Структуры и базы данных. 1986. Оглавление 1. Простые типы данных.. 3 1.1 Целые типы.. 3 1.2 Вещественные типы.. 3 1.3 Логический тип.. 4 1.4 Символьный тип.. 4 1.5 Перечисляемый тип.. 4 1.6 Интервальный тип.. 5 2 Структурированные типы данных.. 6 2.1 Массивы.. 6 2.2 Алгоритмы поиска в массиве. 6 2.3 Записи (структуры) 7 2.4 Битовые множества.. 9 3 Последовательности.. 10 3.1 Операции над последовательностями.. 10 3.2 Последовательный файл. 11 3.3 Файл с прямым доступом.. 12 3.4 Стек. 12 3.5 Очередь. 14 3.6 Дек. 15 4 Сортировка массивов.. 17 4.1 Сортировка массивов. 18 4.1.1 Сортировка вставками. 18 4.1.2 Сортировка простым выбором.. 21 4.1.3 Сортировка простым обменом.. 23 4.1.4 Сортировка Шелла. 26 4.1.5 Пирамидальная сортировка. 29 4.1.6 Быстрая сортировка. 35 4.2. Сортировка файлов. 38 4.2.1 Простое слияние. 38 4.2.2 Естественное слияние. 39 4.2.3 Дальнейшая оптимизация алгоритмов внешней сортировки. 41 5 Рекурсивные алгоритмы... 43 6 Рекурсивные структуры данных.. 46 6.1 Односвязный линейный список. 47 6.2 Двунаправленные и циклические списки.. 49 6.3 Мультисписки.. 49 6.4 Топологическая сортировка.. 50 7 Древовидные структуры... 53 7.1 Бинарные деревья. 57 7.1.1 Обход дерева. 57 7.1.2 Поиск элементов. 59 7.1.3 Включение элементов. 61 7.1.4 Удаление из дерева. 62 7.2 АВЛ-деревья. 63 7.3 Сильно ветвящиеся деревья. 65 7.3.1 B–деревья. 67 8 ГРАФЫ. основные понятия и определения.. 73 8.1 Машинное представление графов. 76 8.1 Поиск в глубину в графе. 82 8.3 Поиск в ширину в графе. 85 8.4 Стягивающие деревья (каркасы) 88 8.5 Фундаментальное множество циклов графа.. 91 8.6 Нахождение компонент двусвязности (блоков) графа.. 96 8.7 Эйлеровы пути.. 101 8.8 Классификация задач по степени сложности.. 106 8.9 Алгоритмы с возвратом.. 109 8.10 Модификации алгоритма с возвратом. задачи на максимум и минимум 113 8.11 Кратчайшие пути.. 119 8.11.1 Алгоритм Форда-Беллмана. 122 8.11.2 Алгоритм Дейкстры.. 124 8.11.3 Пути в бесконтурном графе. 126 8.11.4 Алгоритм Флойда. 130 8.12 Кратчайшие пути с фиксированными платежами.. 132 8.13 Первые K кратчайших путей.. 135 ПРИЛОЖЕНИЕ 1. СПИСОК NP-ПОЛНЫХ ЗАДАЧ.. 138 библиографический список.. 146
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 323; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.148.63 (0.011 с.) |

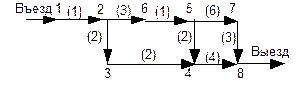


 , …,
, …,  , t.
, t.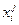 (вершина s имеет номер 1). Будем искать отклонение
(вершина s имеет номер 1). Будем искать отклонение  в этой вершине.
в этой вершине. 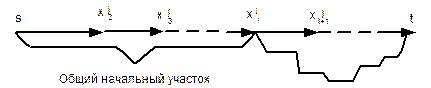
 , …,
, …,  совпадает с начальным участком j-го пути s,
совпадает с начальным участком j-го пути s, 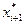 в каждом из этих путей. Для этого в матрицу стоимостей A для всех таких дуг запишем A[
в каждом из этих путей. Для этого в матрицу стоимостей A для всех таких дуг запишем A[  : A[
: A[ 


