
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие графа и его элементыСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Допустим, что участники торгово-экономических связей (A,B,C,D,E,F) заключили между собой договор о взаимных поставках. При этом А обязался поставить свои товары B,C,D,E,F; B – соответственно A,D,E; C, в свою очередь – А И D; D наладил связи с A,B,C; a E-c A,B. Представим участников торгового процесса точками и соединим прямой линией (или дугой) те точки, которые соответствуют участникам, уже заключившим договоры. Это можно изобразить при помощи следующей геометрической схемы (рис. 1.1)
граф G определяется непустым множеством вершин X(G), множеством рёбер V(G) и отношением инцидентности, которое каждому ребру сопоставляет одну или две вершины, называемые его концами. Граф обозначается символом G(X, V). Элементы графа, изображённые точками на плоскости, называются вершинами графа. Таким образом, субъектам торговых процессов будут соответствовать вершины графа. Вершина графа может обозначать и событие, и явление.
Линии, соединяющие любые пары вершин, называются дугами графа или рёбрами графа. Дуги графа должны иметь направления, обозначаемые стрелкой от начала дуги к её концу. Такие графы называются ориентированными. Рёбра не имеют направления. Дуги показывают связь субъектов, последовательность работ, например, при создании супермаркета: проектные, строительные, монтажные, пусконаладочные и другие работы или отношения участников в торговых операциях. Например, А осуществил поставку товаров B(A→B), В рассчитался с А (А←В). Общее число дуг, инцидентных вершине x, является степенью вершины x и обозначается P(x). Для графа, представленного на рисунке 1,1, имеем:
P(A)=5, P(B)=3, P(C)=2, P(D)=3, P(E)=2, P(F)=1. Вершина, степень которой P(x) > 2, называется узлом, а вершина, степень которой P(x) ≤ 2, - антиузлом. Таким образом, вершины A,B,D – узлы, а вершины C,F,E – антиузлы. Имеются понятия: полустепень – захода вершины x – количество дуг, заходящих в данную вершину, P - (x) и полустепень исхода вершины x- количество дуг, исходящих из вершины x, P+(x). В нашем примере степень каждой вершины графа, приведенного на рисунке 1,1, показывает количество партнёров, с которыми заключены договоры. Выделим из всех вершин “нестандартную”, такую, в которую дуга только входит или выходит и причём только одна. Такая вершина называется висячей. В нашем примере ею является вершина F. Такой же “нестандартной” дугой является петля. Это такая дуга, которая выходит из вершины x и входит в неё же, т.е. связывает точку x саму с собой. Пример петли дан на рис. 1.2.
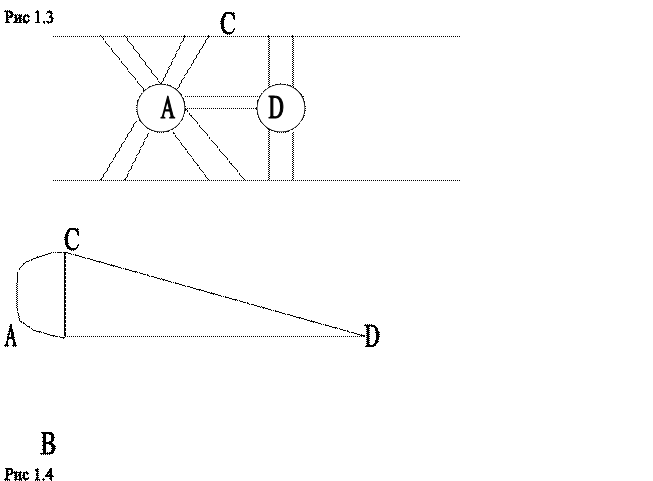
Смысловое значение такой дуги можно представить в случае, если отрасль производит какой-то продукт и сама же его потребляет на собственные нужды. Тогда степень вершины x можно определять как P(x)=1, когда рассматривается вопрос только производства, и P(x)= 2,когда учитывается производство и потребление, т.е. степень вершины с петлей учитывается в зависимости от условий поставленной задачи. С точки зрения ориентации дуг различают: ориентированные графы, в которых вершины соединяются стрелками (дугами), указывающими направления; неориентированные графы, в которых вершины соединяются линиями (рёбрами); смешанные графы, состоящие из дуг и рёбер. Ориентированные графы наиболее информативны. С их помощью можно показать не только взаимосвязь торговых партнёров, но и характер сделки (купли, продажи, расчётов с поставщиком и т.п.). А если каждой дуге присвоить определённое число, то можно отразить количественную или стоимостную характеристику торговой операции. Например, граф A→20→B говорит о том, что A поставил B товаров на 20тыс.руб. Одним из составных элементов графа, получивших довольно широкое применение в экономике, является путь. Под путём понимают последовательность дуг, в которой конец каждой предыдущей дуги совпадает с началом следующей. Длина пути равна количеству дуг(рёбер) в нём, причём каждый элемент пути считается столько раз, сколько встречается. Путь называется простым, если в нём ни одна дуга не встречается дважды, составным, если какая-либо из дуг встречается более одного раза, и элементарным, в котором никакая вершина не встречается дважды. Конечный путь, начинающийся и заканчивающийся в одной и той же вершине, называется контуром. Так же, как и путь, контур может быть простым, если в нём ни одна дуга не встречается дважды, и сложным – в противном случае. Следует иметь ввиду, что в неориентированных графах вместо пути принято употреблять слово цепь, а вместо контура – цикл. Понятие пути используется наиболее часто при решении транспортных задач, при размещении коммуникаций, при определении рациональных потоков товаров или покупателей и т.п. Остановимся на двух задачах, вошедших в классику теории графов. В первой задаче используется понятие простого пути. Её сформулировал известный математик Леонард Эйлер (1707-1783) в первой работе о графах. Он рассмотрел “задачу о кёнигсбергских мостах” (части города были соединены семью мостами). Задача состояла в том, что чтобы выйдя из дома вернуться обратно, пройдя только один раз по каждому мосту. Решение этой задачи привело к формулировке общей проблемы теории графов: “ На каких графах можно найти цикл, содержащий все рёбра графа, причём каждое ребро в точности по одному разу?”. Такой цикл получил название эйлеровой линии, а граф, обладающий эйлеровой линией, - эйлеровым графом. Признаком наличия эйлеровой линии является честность степеней всех вершин графа. На рисунке 1.3 приведён исходный граф а на рисунке а на рисунке 1.4 - преобразованный граф задачи Эйлера.
Вторую задачу поставил ирландский математик У.Гамильтон. Его именем назван Граф, содержащий цикл, включающий каждую вершину этого графа 1 раз. Такой цикл назвали гамильтоновым. Это понятие применяется в задаче о коммивояжере. Район, который должен посетить бродячий торговец, содержит какое-то количество городов расстояния между ними известны, и нужно найти кратчайшую дорогу, проходящую через все пункты и возвращающуюся в исходное положение. К этой формулировке сводятся задачи о лучшем использовании транспортных средств. Признаки наличия гамильтоновского цикла ещё не сформулированы строго.
Разновидности графов
Граф G(X,V), состоящий только из изолированных вершин, называется нуль-графом. Для него справедливо P+(xi)= P-(xi) = 0 для всех xi ϵ X. Однородный граф – это граф, в котором степени всех вершин одинаковы. Симметрический граф – граф, в котором любые две смежные вершины соединены двумя противоположно ориентированными дугами. Здесь справедливо: если (x1,x2)ϵV, то и (x2,x1)ϵV. Антисимметрический граф – это граф без петель, в котором каждая парасмежных вершин соединена только в одном направлении. Для него справедливо: если (x1,x2)ϵ V, то (x1,x2)ϵ.
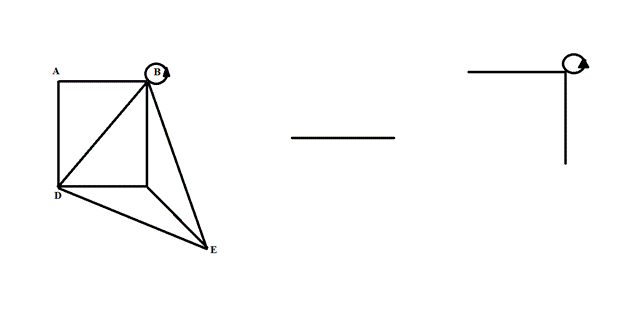
Полный граф – это граф, в котором любая пара вершин соединена дугой(многоугольник, у которого проведенены все диагонали, а у каждой вершины имеется петля). Имея некоторый граф (рис 1.5), можно всегда превратить его в полный с теме же вершинами, добавлением недостающих дуг и петель. Это новый граф будем называть дополнением графа G (рис. 1.6) и обозначать его G. Объединение графов G и G даёт полный граф с теми же вершинами.
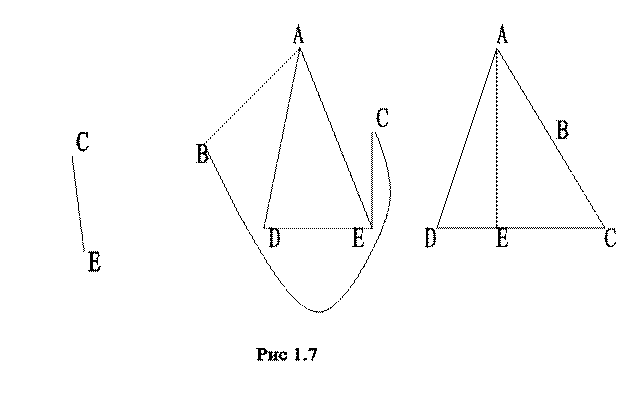
Мультиграф – граф, в котором хотя бы две смежные вершины соединены более чем одной дугой (ребром) в одном и том же направлении. Наиболее число дуг (рёбер), соединяющих смежные вершины, определяет его кратность. Изоморфные графы. Любой граф G(X, V) можно изображать по-разному: не обязательно изображать его рёбра (дуги) прямыми линиями, можно произвольно располагать вершины на плоскости. Говорят, что графы изоморфны, если: они имеют одно и тоже число вершин: две любые вершины одного графа соединены ребром, то и соответствующие им вершины другого графа тоже соединены. Термин ”изоморфный“ иос - равный, одинаковый и морфии-вид, форма часто используется в математике. В одном случае это графы, равные по форме, на рис.1.7 изображены изоморфные графы.
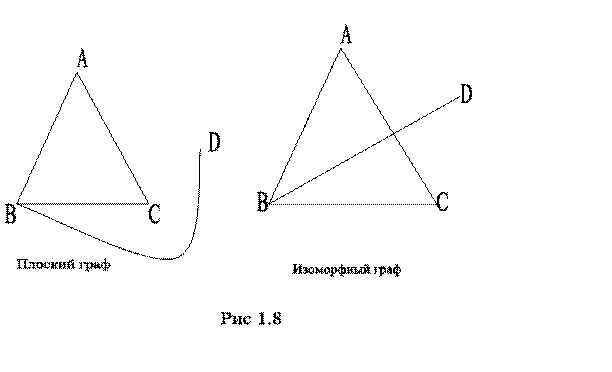
Плоский граф – такой граф, который можно изобразить на плоскости так, чтобы никакие два ребра не пересекались в точках отличных от вершин. Необходимо помнить, что изоморфный ему граф тоже будет плоским, хотя его рёбра могут при изображении и пересекаться. На рис. 1.8 показан плоский граф и граф изоморфный ему. Плоские графы используются для моделирования непересекающихся.
Двудольный граф – граф, представленный двумя множествами M и P,вершины которых внутри каждого множества не соединены между собой ребрами (рис. 1.9). R
1 2 3 m M Рис.1.9 С помощью двудольных графов решаются такие задачи, как назначение на должности, определение степени соответствия товара требованиям покупателей или ГОСТа и другие аналогичные задачи на соответствия.
Операции над графами Подграфом графа G (X,V) называется граф G(A, 1. Вершины А подграфа G(A, 2. Дугами (ребрами) подграфа G(A, Подграф G(A,
а)Граф G(X,V) б)подграф G(A, Рис.1.11
Подграфы эффективно применяются в многошаговых задачах, которые имеют сложный разветвленный так называемый сетевой граф. Верхним сечением V+(A) некоторого подмножества А вершин графа < X, V > называется подграф <B, Удаление вершины или ребра – это операции, с помощью которых можно из имеющегося графа получить другие графы с меньшим числом элементов. Добавление ребра – если вершины Объединение – граф H будет объединением (или наложением) графов G и F, если VH=VG
Рис.1.12 Произведение
Рис.1.13 Отождествление (слияние) вершин. Пусть
Стягивание ребра означает отождествление смежных вершин (рис. 1.14)
Рис.1.14 Расцепление вершин – операция, двойственная стягиванию ребра (рис. 1.15)
Рис.1.15 Древовидные графы и сети Понятие связности графа В общем случае граф может быть представлен отдельными графами, не имеющими общих дуг. Например, граф G(X,V) может быть задан в виде трех графов: Граф связан в том и только в том случае, если он состоит из единственной компоненты связности. Таким образом, если каждую вершину графа можно соединить с любой другой вершиной некоторой цепью (путем), то граф называется связным (рис.2.1).
Рис.2.1 Несвязный граф, состоящий из четырех связных компонент, одна из которой – изолированная вершина 5.
X2 X6
X4
Рис.2.2
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 456; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.22.184 (0.008 с.) |




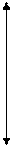






















 ),определяемый следующим образом.
),определяемый следующим образом.










 >
> > (в).
> (в). и
и  графа не смежны, то можно определить граф G+L, где L
графа не смежны, то можно определить граф G+L, где L  ). Он получается из графа G добавлением ребра L.
). Он получается из графа G добавлением ребра L.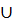 VF и XH= XG
VF и XH= XG 






 есть граф, для которого VG=
есть граф, для которого VG=  (рис. 1.13).
(рис. 1.13).


 , соединив ее с каждой из вершин, входящих в объединение окружений вершин
, соединив ее с каждой из вершин, входящих в объединение окружений вершин 






 2 2
2 2


 1 3 1 3
1 3 1 3
 4
4 
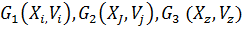 , в которых
, в которых  ⊂ X,
⊂ X,  ⊂ X,
⊂ X,  ⊂ X, и
⊂ X, и  ⊂ V,
⊂ V,  ⊂ V,
⊂ V,  ⊂ V. В этом случае граф G(X, V) называется несвязным, а каждый из составляющих его графов
⊂ V. В этом случае граф G(X, V) называется несвязным, а каждый из составляющих его графов  - компонентами связности. Другими словами, компонента связности графа G(X, V) – это граф, состоящий из вершин x
- компонентами связности. Другими словами, компонента связности графа G(X, V) – это граф, состоящий из вершин x  X и всех тех вершин, которые соединены с ней (компонентой) некоторой цепью. Компоненты связности образуют разбиение множества вершин x графа G(X, V) на отдельные, не связанные друг другом подмножества.
X и всех тех вершин, которые соединены с ней (компонентой) некоторой цепью. Компоненты связности образуют разбиение множества вершин x графа G(X, V) на отдельные, не связанные друг другом подмножества.





 X1 X3 X5
X1 X3 X5


