
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способы представления графов: аналитический, графический и матричный.Содержание книги
Поиск на нашем сайте
Определение 2. Вершины xi и xj графа G = (X, U) называются смежными, если (i, j)? U Определение 3. Дуга (i, i)? U - называется петлей. Определение 4. Вершина xi? X и дуга (i,j)? U инцидентны, если xi есть конец ребра (i,j).
Определение 5. Степень вершины xi - это число инцидентных ей ребер.
Утверждение. В любом неориентирном графе G без петель с n вершинами и m ребрами имеет место
Следствие. Число вершин с нечетными степенями всегда четно.
Утверждение. Если G- орграф без петель с n вершинами и m дугами, то:
Матричные представления графов. Графы можно задавать не только аналитическим и графическим способом, но и с помощью матриц.
Определение. Матрицей смежности Ag = {aij) графа G = (X, U) называется квадратная матрица порядка n, элементы которой определяются зависимостью:
 1, если в G существует дуга (i,j) (xi,xj смежны) 1, если в G существует дуга (i,j) (xi,xj смежны)
0, если в G нет дуги (i,j) (xi,xj не смежны) Пример
 
Матрица смежности полностью определяет структуру графа. Например, сумма всех элементов строки Xi матрицы Ag дает полустепень исхода
1, если Хi является начальной вершиной дуги Uj,
0, если Хi не является вершиной дуги Uj, 2, если Uj является петлей.
Поскольку каждая дуга инцидента двум различным вершинам за исключением того случая, когда дуга образует петлю, то каждый столбец либо содержит один элемент, равный 1, и один - равный - 1, либо все элементы столбца = 0. Если G является неориентированным графом, то его матрица инциденций определяется также как и выше за исключением того, что все элементы, равные - 1 заменяется на + 1.
Аналитическое задание графа – перечень всех его вершин и дуг: Пути и маршруты
Дуги Uk=(Xi,Xj) и Ul=(Xj,Xr), имеющие общие концевые вершины, называются смежными. Две вершины Xi и Xj называются смежными, если какая-нибудь из двух дуг (Xi, Хj) и (или) (Xj, Xi) одновременно присутствуют в графе. Например, дуги U1,U10 и U3,U6; вершины Х3,Х5, смежны. Дуги U1,U8 и вершины Х1,Х4 не являются смежными. Орцепью называют такой путь, в котором каждая дуга используется не более одного раза. Например, (1) и (2) - орцепь; (3) - не орцень, т.к. U6, - дважды включена в путь. Простой орцепью (элементарным путем) называют такой путь, в котором каждая вершина используется не более одного раза. (2) - простая орцепь, пути (1) и (3) - не простая орцепь. Маршрутом называют последовательность ребер U1, U2…Un, в которой каждое ребро Ui, за исключением первого и последнего ребер, связано с ребрами Ui-1 и Ui+1 своими двумя концевыми вершинами. Различают простые и элементарные маршруты Маршруты: Черта над символом означает. что ориентацией пренебрегают
Пример 3.1. Записать граф G = (X,U) аналитически, построить матрицы смежности, инциденций, пропускных способностей дуг и достижимостей. Определить экстремальные значения путей и маршрутов.
Решение. 1. Запишем граф G = (U, X) аналитически X = (Xi, Х2, X3, X4, X5. X6) U=(U1=(X1,X2);U2=(X2,X3);U3=(X2,X4);U4=(X3,X4);U5=(X5,X4); U6 =(X4,X6);U7=(X6, X5);U8=(X1, X5);U9=(X5,X5)), где X - множество вершин, a U - множество дуг. 2.Строим матрицу смежности А.g.
где α- и α+ полустепени исхода и полустепени захода вершин Хj соответственно. 3.Составляем матрицу инциденций В= { bik }. Матрица инциденций В –это прямоугольная матрица размером m x n, где m – число вершин, n – количество дуг, элементы которой определяются:
1, если Xi является начальной вершиной дуги Uk bik =, -1. если Xi является конечной вершиной дуги Uk 0, если Xi не является вершиной дуги Uk 2, если Uk является петлей.
3. Составляем матрицу пропускных способностей дуг С={cik}, которая строится на основе матрицы смежности A, заменяя элементы равные 1 соответствующим значением пропускной способности дуги. 4.
5. Строим матрицу достижимостей D= {dik}, которая определяется следующим образом:
0, в противном случае
6. Определяем пути их Х
Сети Сеть – конечный граф G(X,V) без циклов и петель, ориентированный в одном направлении от вершин V, являющихся входом графа, к вершинам W, являющихся выходами. При этом для каждой вершины V полустепень захода, а для каждой вершины W полустепень исхода, равна нулю, т.е P(V)=P(W)=0 Наибольшее распространение среди множества сетей получила транспортная сеть, которая имеет только вход и выход. Каждой дуге такой сети соответствует целое число C (ν) ≥ 0, называемое пропускной способностью дуги ν (рис 2.8)
Рис.2.8 Поток сети - это некоторая функция ϕ (ν), удовлетворяющая условиям: 1) φ(ν) ≥ 0, (ν 󠅳 2) φ(ν) ≤ С (ν); 3) ∑ φ (ν) - ∑ φ (ν) = 0 ν
Это означает, что функция Ф (ν), где поток по дуге ν, есть целочисленное положительное число, которое не превышает пропускной способности данной дуги; сумма потоков, входящих в некоторую вершину ∑ φ(ν) - ∑ φ (ν) = Ф ν где ϕ Для анализа пропускной способности сети используется понятие разрез сети. Все множества вершин 1) A ≠B, A 2) V 3) W Следовательно, в подмножестве А содержится вход сети и некоторые промежуточные вершины. Подмножество В, содержит все остальные вершины и в том числе выход сети W. Подмножество дуг С ( Например, разрез Ӏ (рис. 2.8) определяется множеством верши A = { Пропускной способностью C ( Поток φ (ν), проходящий по данной дуге не может превышать пропускную способность дуги С(ν), а, следовательно, его максимальная величина является φ (ν) = V(ν). В этом случае дуга называется насыщенной. Из всех разрезов сети можно выделить один, который обладает наименьшей пропускной способностью С ( Наибольшая величина потока
Для транспортной сети введено понятие рангов ее вершины, отражающих последовательность формирования потоков через каждую вершину. Более высокий ранг вершины показывает, что в формировании потока через нее участвуют потоки, проходящие через вершины более низкого ранга. Ранги вершин проставляются по восходящей от входа к выходу сети так, что каждая последующая вершина имеет ранг восходящий по назначению, чем ранг всех предыдущих ее вершин. Пример 3.2. определить величину максимального потока и указать минимальный разрез
Рис. 3.4 Решение. 1. Составим матрицу пропускных способностей дуг для сети
Укажем один из путей из вершины
Рассмотрим второй путь из
Аналогично получаем остальные матрицы.
Указать путь из вершин
сеть с максимальным потоком.
Минимальным разрезом является величина
Равновесие узлов
Поток входящий в каждый узел равен потоку, выходящему из него (равновесие узлов).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 716; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.56.71 (0.006 с.) |


 - степень вершины i
- степень вершины i


 Орграф.
Орграф.
 - полустепень исхода
- полустепень исхода
 - полустепень захода
- полустепень захода


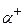 вершины Xi, a сумма элементов столбца Хk - дает полустепень захода вершины Хk -
вершины Xi, a сумма элементов столбца Хk - дает полустепень захода вершины Хk -  .
. Определение. Матрица инциденций графа G = (X, U) (обозначается В = (bij)) является матрица размерности m x n, элементы которой определяются следующим образом:
Определение. Матрица инциденций графа G = (X, U) (обозначается В = (bij)) является матрица размерности m x n, элементы которой определяются следующим образом:
 (1)
(1)
 (2)
(2)
 (3)
(1)-(3)-пути
(3)
(1)-(3)-пути



 2
2

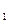 в Х
в Х  , (без учета петли)
, (без учета петли)


 V);
V); V
V  ν
ν  (не являющуюся входом или выходом), равна сумме потоков, выходящих из этой вершины.
(не являющуюся входом или выходом), равна сумме потоков, выходящих из этой вершины.
 ν
ν  - величина суммарного потока через вершину
- величина суммарного потока через вершину  .
. x и B
x и B  x;
x; , заходящих в В, называется разрезом сети, а сумм пропускных способностей этих двух составляет пропускную способностьразреза
, заходящих в В, называется разрезом сети, а сумм пропускных способностей этих двух составляет пропускную способностьразреза 
 }, B = {
}, B = {  }, дуг
}, дуг  }
}
 , т.е. разрез минимальной величины.
, т.е. разрез минимальной величины. не может быть более минимального разреза сети, т.е.
не может быть более минимального разреза сети, т.е. = С (
= С ( для сети (рис. 3.4.)
для сети (рис. 3.4.)
 (рис.3.4)
(рис.3.4)
 =
=

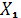 в вершину
в вершину  . Например,
. Например,  , отмечаем значения соответствующих пропускных способностей дуг в матрице
, отмечаем значения соответствующих пропускных способностей дуг в матрице  чертой над числами:
чертой над числами:  . Определим минимальное из них, т.е.
. Определим минимальное из них, т.е.  Величину
Величину  вычитаем из чисел {6,5,10} в матрице
вычитаем из чисел {6,5,10} в матрице  .
.


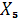


 = 1. Величину
= 1. Величину  вычитаем из чисел {1, 3, 12} в матрице
вычитаем из чисел {1, 3, 12} в матрице  .
.







 больше нельзя. Составим матрицу
больше нельзя. Составим матрицу  из соответствующих элементов матрицы
из соответствующих элементов матрицы  . величину максимального потока определим из условия:
. величину максимального потока определим из условия: Рис. 3.5.
Рис. 3.5. (рис.3.4)
(рис.3.4) проверяем на сети с максимальным потоком:
проверяем на сети с максимальным потоком:



