
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коды, определенные на графахСодержание книги Поиск на нашем сайте
Глава 1 Введение Данная работа связана с анализом, кодированием и декодированием очень мощного и гибкого семейства кодов, контролирующих ошибки, называемых LDPC кодами (low-density parity-check codes - проверочные коды с низкой плотностью проверок). LDPC коды могут быть использованы для различных типов каналов с практической сложностью декодирования. Предполагалось, что они могут обеспечивать максимальную пропускную способность для различных типов каналов и, действительно, позже была доказана их способность обеспечить пропускную способность BEC канала (binary erasure channel - двоичный канал со стиранием), с помощью итеративного декодирования. В этой главе рассматриваются некоторые понятия, которые исследуются в диссертации. Мы обсудим важность области исследования, интересные задачи, которые привлекают исследователей в этой области и некоторые нерешенные проблемы.
Коды, определенные на графах С 1948 года, когда Клод Шеннон ввел понятие пропускной способности канала [1], конечная цель теории кодирования заключалась в том, чтобы найти практический потенциал пропускной способности кодов. В соответствии с теоремой Шеннона о пропускной способности канала, надежная связь на скорости
где Подойти к пределу Шеннона в несколько децибел (дБ) стало возможным благодаря практической сложности декодирования, с помощью сверточных кодов, но сокращение этого интервала требовало нереальной сложности до открытия турбо кодов [2]. Одним из важных нововведений в турбо кодах стало введение классов с низкой сложностью неоптимальных правил декодирования, т.е. итеративных алгоритмов передачи сообщений. Использование итеративного декодера передачи сообщений, турбо кодов обеспечивает малую вероятность ошибочного декодирования и небольшой интервал до предела Шеннона с низкой (практической) сложностью декодирования. На рис. 1.1 приведены типичные результаты вероятности ошибочного декодирования турбо кода и сверточного кода при передаче по каналу связи с аддитивным белым гауссовским шумом (см. [3, рис. 5], например). Эта удивительная низкая вероятность ошибочного декодирования турбо кодов обратила большое внимание к данной области исследования, которая вскоре расширилась на более широкий класс кодов называемых кодами, определенными на графах. Коды, определенные на графах, могут быть декодированы алгоритмами передачи сообщений. Двумя важными особенностями декодирования такого типа, которые делают коды, определённые на графах, такими привлекательными являются близкая к оптимальной вероятность ошибочного декодирования и ее практическая сложность (для фиксированного числа итераций), которая возрастает линейно с длиной кода. Это, в свою очередь, позволяет использовать очень длинные коды. Таким образом, теперь, после 50 лет после работ Шеннона, специалисты кодирования могут найти коды вероятностью ошибочного декодирования близкой к пределу Шеннона и с разумной сложностью декодирования. Кроме того, для некоторых каналов они узнали, как может быть достигнута пропускная способность, хотя декодер и требует усложнения, так как вероятность ошибочного декодирования кода приближается к пропускной способности.
Обзор главной темы
LDPC коды являются одними из наиболее важных кодов, определённых на графах. Всё это из-за их малой вероятности ошибочного декодирования и гибкой структуры. Как уже упоминалось выше, многие коды, определённые на графах, были подвержены влиянию структурой LDPC кодов. Это делает исследование LDPC кодов центральным в этой области. LDPC коды уже используются в таких стандартах, как ETSI EN 302 307 для цифрового видео вещания [26] и IEEE 802.16 (Вещательное Рабочее Сообщество Беспроводного доступа) для кодирования OFDMA систем (orthogonal frequency division multiplexing access systems - ортогональные системы частотно-мультиплексного доступа) [27]. В области LDPC кодирования всё ещё остаётся много открытых вопросов. Данная работа ответит на многие вопросы, но в свою очередь откроет целый ряд новых.
Главная тема данной работы
В данной работе описываются эффективные методы кодирования и анализа LDPC кодов, а также их декодирования. Эти проблемы изучаются с практической точки зрения, а также будет поднят ряд новых интересных вопросов. Некоторые из этих вопросов получат ответ в данной работе, а некоторые останутся в качестве открытых. В данной работе рассматриваются три основные проблемы:
• эффективные методы кодирования неравномерных LDPC кодов;
Такая низкая вероятность ошибочного декодирования достигается за счет тщательной разработки неравномерности кода. К сожалению, за исключением нескольких случаев, эти методики расчета могут быть насыщены вычислениями. Традиционный метод кодирования заключается в создании некоторой неравномерности в коде, проверяющей работу с плотностью эволюции, и изменении неравномерности в коде до желаемой вероятности ошибочного декодирования. Интересная проблема, которая рассматривается в литературе, заключается в упрощении методики расчета LDPC кодов [24]. Это будет одним из основных направлений этой работы.
Рис. 1.2. Сравнение вероятностей ошибочного декодирования уровней ½ LDPC кодов различной длины с турбо кодами одинаковой длины.
Построение менее сложных алгоритмов декодирования является другой целью исследователей в этой области. Мы будем решать эту важную проблему в данной работе и покажем, что, имея существующие алгоритмы, менее сложные варианты декодирования возможны, просто позволяя декодеру выбрать правила декодирования среди множества предопределенных правил. Мы называем это декодирование методом переключения передач, так как декодер переключает передачи (изменяет правила декодирования) в целях ускорения декодирования. Другой открытой фундаментальной проблемой является получение наименьшей вероятности ошибочного декодирования. Мы изучаем эту проблему в особом случае, когда требуется определенная конвергенция. Мы находим некоторые свойства самой высокой скорости LDPC кода, которая гарантирует желаемую конвергенцию. Мы также рассмотрим некоторые практические проблемы, такие как применение LDPC кодов в частотно-селективных каналах. Мы покажем, что LDPC коды имеют некоторые особенности, которые делают их хорошим выбором для кодирования при передаче по таким каналам.
Организация данной работы В главе 2 мы обеспечим необходимый базис, в общих чертах характеризующий LDPC коды, алгоритмы их декодирования и существующие методы анализа этих алгоритмов декодирования. В главе 3 мы ознакомимся с LDPC декодированием с использованием алгоритмов двоичной передачи сообщений. Мы отслеживаем сообщение об ошибочной скорости, чтобы проанализировать декодер и изобразить EXIT диаграммы, основанные на сообщениях об ошибочной скорости. Также доказано, что алгоритм В Галлагера является, возможно, лучшим бинарным алгоритмом передачи сообщений. Мы используем EXIT диаграммы для разработки неравномерных LDPC кодов и, для того чтобы показать, что процесс кодирования может быть позиционирован в качестве линейного программирования. В главе 4 мы продолжим анализ главы 3. Опять же, мы используем EXIT диаграммы, основанные на сообщениях об ошибочной скорости, и покажем, как могут быть получены точные EXIT диаграммы. В то время как предыдущие работы по анализу LDPC кодов в AWGN каналах использовали наработки Гаусса для сообщений [24], мы избегаем предположений Гаусса о выходах проверочных узлов, которые на самом деле являются плохими предположениями. Мы называем наш метод «наполовину Гаусса», в отличие от «полного» метода Гаусса, который принимает все гауссовы сообщения. Мы показываем, что очень точный анализ и кодирование LDPC кодов можно осуществить с помощью приближения метода Гаусса. Опять же, мы используем EXIT диаграммы, чтобы уменьшить методику расчета неравномерных LDPC кодов до линейного программирования. Мы также дадим несколько советов по кодированию таких кодов. По сравнению с кодами, кодированными с помощью анализа плотности эволюции, наши коды будут выполнены всего лишь на несколько сотых долей дБ хуже. В главе 5 мы рассмотрим класс алгоритмов декодирования, для которых анализ EXIT диаграмм декодера является точным (или имеет хорошее приближение). Мы рассматриваем общий случай кодирования кодов для желаемого поведения конвергенции и обеспечиваем необходимые и достаточные условия, для того чтобы были EXIT диаграммы удовлетворяли условию максимальной скорости LDPC кодов. Наши результаты обобщают некоторые из существующих результатов ВЕС. В главе 6 мы применяем неравномерные LDPC коды для разработки многоуровневых схем кодирования с последующим их применением в DMT системах (discrete multi-tone systems - дискретные мультитональные системы). Мы используем комбинированную маркировку Грея/Ангербёка для QAM. Биты, маркированные по Грею, защищены, благодаря неравномерным LDPC кодам, в то время как другие биты защищаются с помощью высокой скорости кода Рида-Соломона с жёстким решением декодирования (или остаются не кодированными). Скорость LDPC кодов выбирается на основе анализа пропускной способности канала. Затем мы применяем эту схему кодирования для ансамбля частотно-селективных каналов с гауссовским шумом. Эта схема кодирования обеспечивает эффективное кодирование с приростом более чем на 7,5 дБ при вероятности ошибки В главе 7 мы рассматриваем декодирование методом переключения передач, в котором итерационный декодер может выбирать правила декодирования среди групп алгоритмов декодирования на каждой итерации. Сначала покажем, что при правильном выборе алгоритма на каждой итерации задержка декодирования может существенно снижаться. Мы покажем, что задача нахождения декодера с оптимальным переключением передач (минимальной задержкой декодирования) может быть позиционирована в качестве динамической программы. Затем мы предложим конструкцию канала связи и оптимизируем декодер с методом переключения передач для достижения минимальной стоимости оборудования вместо минимальной задержки. В главе 8 мы предоставим краткий обзор данной работы и некоторые предложения для будущих работ.
Глава 2 LDPC коды и их анализ Целью этой главы является рассмотрение необходимых сведений о LDPC кодах, их структуры, алгоритмов декодирования и существующих методов анализа этих алгоритмов декодирования.
LDPC коды: структура
LDPC код является линейным блочным кодом и, поэтому имеет проверочную матрицу. Существенным отличием LDPC кодов от обычных линейных кодов является матрица проверки четности, в которой число ненулевых элементов на много меньше, чем общее число записей, которые могут быть найдены для неё. Графическое представление LDPC кодов настолько популярно, что большинство людей думает и говорит о LDPC кодах с точки зрения структуры их фактор графов. Как упоминалось ранее, графическое представление линейных кодов началось с графов Таннера [4]. Здесь мы сосредоточимся на фактор графах, в связи с их более общим характером происхождения. Фактор граф всегда является двудольным графом, вершины которого разбиты на переменные узлы и функции (проверки) узлов [29,35]. Мы считаем удобным взять двудольный граф и показать, как двоичный линейный код может быть из него сформирован. Рассмотрим двудольный граф Q с n левыми узлами (назовем их переменными узлами) и r правыми узлами (назовем их проверочными узлами) и E дугами. На Рис. 2.2 показан пример такого двудольного графа. Обратите внимание, что на этом рисунке переменные узлы показаны кружками, а проверочные узлы - квадратами, так же, как и для всех фактор графов. Переменный узел
где В результате получается двоичный линейный код длины LDPC коды могут быть расширены до Это легко объясняется, если предположить, что любой двудольный граф LDPC коды, в зависимости от их структуры, могут быть классифицированы, как равномерные или неравномерные. Равномерные коды имеют переменные узлы с фиксированными степенями и проверочные узлы с фиксированными степенями. Обозначая степень переменных узлов, как
Таким образом, скорость кода R может быть вычислена, как
Если строки Теперь рассмотрим ансамбль равномерных LDPC кодов с переменной степенью Хотя показатели равномерных LDPC кодов близки к пропускной способности, у них имеется большой интервал от пропускной способности, в отличие от турбо кодов. Основное преимущество равномерных LDPC коды над турбо кодами заключается в их лучшей, так называемой, "ошибке нижнего уровня". Из Рис. 1.2 видно, что, по сравнению с низкими SNR, BER кривая турбо кодов для умеренных и высоких SNR имеет меньший наклон. Это явление называется "ошибкой нижнего уровня". Рис. 3 в [36] отображает качественное поведение BER кривой относительно LDPC коды стали более привлекательными, когда Люби с коллегами показал, что разрыв пропускной способности может быть сокращен с помощью неравномерных LDPC кодов [17]. LDPC код называется неравномерным, если на его фактор графе не все переменные (и/или проверочные) узлы имеют равные степени. Тщательно кодируя неравномерность графа, можно получить коды с показателями, очень близкими к пропускной способности [13,17,21,28]. Ансамбль неравномерных LDPC кодов определяется его переменным распределением степеней дуг На подобие равномерным кодам, в [12] показано, что обычное поведение ансамбля неравномерных кодов, почти во всех случаях сосредоточено вокруг ожидаемого поведения, когда код достаточно велик. Кроме того, ожидаемое поведение сводится к случаю без циклов [12]. Учитывая степень распределения LDPC кода и число дуг
и число проверочных узлов
Поэтому кодируемая скорость кода будет
или, что эквивалентно
Поиск “хорошего” асимптотически длинного семейства неравномерных кодов эквивалентен поиску “хорошей” степени распределения. Очевидно, что для различных приложений, различные атрибуты будут являться предпочтительными. Задача поиска степени распределения, которая в результате даёт семейство кодов с определёнными нужными свойствами, не является тривиальной задачей и является одной из основных задач данной работы. Мы попытаемся сформулировать представление семейства кодов с точки зрения степени его распределения в простой форме, чтобы обеспечить максимальную гибкость на стадии кодирования, и в то же время избежать излишнего упрощения, чтобы наши полученные результаты в итоге были близки к реальным.
LDPC коды: декодирование
Из (2.4) видно, что, фиксируя переменную степень распределения кода, число дуг в фактор графе такого кода пропорционально n. Это важное свойство LDPC кодов, которое создает их декодирующую сложность линейно с длиной кода, с учетом фиксированного числа итераций. Это связано с тем, что декодирование производится путем передачи сообщения по дугам графа, следовательно, сложность одной итерации будет порядка Е. Есть много различных алгоритмов передачи сообщений для LDPC кодов. Целью данного раздела является представление некоторых из этих алгоритмов декодирования. Мы начнем с алгоритма sum–product и, используя интерпретацию декодирования методом sum-product, нам станут понятны другие алгоритмы декодирования.
Алгоритм sum-product
В приложение A описывается алгоритм sum-product в общем виде. Рассматривая основную цель этой главы, мы ориентируемся на упрощенный случай, в котором переменные узлы имеют двоичное значение и функциональные узлы ограничены контролем четности. Не вдаваясь в детали, определим характер сообщений и упрощенные правила их корректировки. Затем мы используем это, чтобы сформировать объяснение декодирования LDPC кодов методом передачи сообщений. Для двоичных переменных узлов сообщение Правило корректировки узла контроля четности
где Правило корректировки переменного узла
где На рис. 2.3 показан фактор граф LDPC кода в декодере. Здесь показаны внутренние и внешние сообщения на переменный узел MAP решение (примерное MAP решение соответствует наличию циклов) для переменного узла
Если В оставшейся части этой работы, когда мы ссылаемся на алгоритм sum-product, мы имеем в виду упрощенный случай для двоичного кода с контролем четности, если не указано иное. Рис. 2.3. Внутренние и внешние сообщения на переменном узле
LDPC коды: анализ
Прежде чем изучать методы анализа LDPC кодов, мы обсудим принцип итеративного декодирования, чтобы стала ясна цель такого анализа.
Рис. 2.4. Принцип итеративного декодирования. Итеративный декодер на каждой итерации использует два источника информации передаваемого кодового слова: информация из канала (внутренняя информация), а также информацию из предыдущей итерации (внешняя информация). От этих двух источников информации алгоритм декодирования пытается получить более качественную информацию о передаваемом кодовом слове, с помощью этих данных как внешней информации для следующей итерации (см. рис. 2.4). В успешном декодировании внешняя информация становится все лучше и лучше по мере того, как декодер производит итерацию. Таким образом, во всех методах анализа итеративного декодера статистика внешних сообщений на каждой итерации изучаема. Изучение эволюции PDF-функций из внешних сообщений, по очереди перебирая каждую итерацию, представляет собой наиболее полный анализ (известный как плотность эволюции). Однако, в качестве приближенного анализа можно проследить за эволюцией представителей этой плотности.
Анализ LDPC кодов Галлагера
В первоначальных работах Галлагера LDPC коды считались равномерными и декодирование предполагало использование двоичных сообщений (алгоритмы А и Б). Галлагер проводил анализ декодера в таких ситуациях [11]. Основной идеей его анализа является характеристика величины ошибок в сообщениях в каждой итерации с точки зрения ситуации в канале и величины ошибки в сообщениях в предыдущей итерации. Другими словами, при анализе Галлагера, эволюция величины ошибки в сообщениях изучаема, она также эквивалентна плотности эволюции, потому что PMF-функция двоичных сообщений является одномерной, т. е. она может быть описана одним параметром. Рис. 2.5. Дерево декодирования глубины один для равномерного (3, 6) LDPC кода. Анализ Галлагера базируется на предположении, что входящие сообщения на переменный (проверочный) узел являются независимыми. Хотя это предположение верно, только если граф без циклов, это доказано в [12], где ожидаемая вероятность ошибочного декодирования кода сводится к случаю без циклов по мере увеличения длины блока кода.
Дерево декодирования
Рассмотрим скорректированное сообщение от переменного узла Рис. 2.6. Дерево декодирования глубины два для неравномерного LDPC кода.
Обратите внимание, что, когда фактор граф является деревом, сообщения в дереве декодирования любой глубины независимы. Если фактор граф имеет циклы и его объем
Глава 1 Введение Данная работа связана с анализом, кодированием и декодированием очень мощного и гибкого семейства кодов, контролирующих ошибки, называемых LDPC кодами (low-density parity-check codes - проверочные коды с низкой плотностью проверок). LDPC коды могут быть использованы для различных типов каналов с практической сложностью декодирования. Предполагалось, что они могут обеспечивать максимальную пропускную способность для различных типов каналов и, действительно, позже была доказана их способность обеспечить пропускную способность BEC канала (binary erasure channel - двоичный канал со стиранием), с помощью итеративного декодирования. В этой главе рассматриваются некоторые понятия, которые исследуются в диссертации. Мы обсудим важность области исследования, интересные задачи, которые привлекают исследователей в этой области и некоторые нерешенные проблемы.
Коды, определенные на графах С 1948 года, когда Клод Шеннон ввел понятие пропускной способности канала [1], конечная цель теории кодирования заключалась в том, чтобы найти практический потенциал пропускной способности кодов. В соответствии с теоремой Шеннона о пропускной способности канала, надежная связь на скорости
где Подойти к пределу Шеннона в несколько децибел (дБ) стало возможным благодаря практической сложности декодирования, с помощью сверточных кодов, но сокращение этого интервала требовало нереальной сложности до открытия турбо кодов [2]. Одним из важных нововведений в турбо кодах стало введе
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 622; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.15.91 (0.011 с.) |

 (бит / канал использования) по AWGN каналу (additive white Gaussian noise channel - канал с аддитивным белым гауссовским шумом) обеспечивается при определенном минимальном уровне сигнал-шум, называемом пределом Шеннона. В условиях нормированного уровня
(бит / канал использования) по AWGN каналу (additive white Gaussian noise channel - канал с аддитивным белым гауссовским шумом) обеспечивается при определенном минимальном уровне сигнал-шум, называемом пределом Шеннона. В условиях нормированного уровня  отношения битов энергии к плотности шума, надежная связь может иметь место при условии скорости
отношения битов энергии к плотности шума, надежная связь может иметь место при условии скорости 
 есть средняя энергия, затрачиваемая на один переданный бит,
есть средняя энергия, затрачиваемая на один переданный бит,  есть средняя дисперсия или спектральная плотность шума. Требуемый минимум
есть средняя дисперсия или спектральная плотность шума. Требуемый минимум  и
и  с турбо кодами равной длины при передаче по каналу связи с аддитивным гауссовским шумом. Турбо коды могут превзойти LDPC коды на коротких длинах блоков, но как можно увидеть из рис. 1.2, если длина блока является большой (как правило, более 5000), неравномерные LDPC коды превосходят турбо коды равной длины. С увеличением длины кодов улучшается вероятность ошибочного декодирования. LDPC коды длиной
с турбо кодами равной длины при передаче по каналу связи с аддитивным гауссовским шумом. Турбо коды могут превзойти LDPC коды на коротких длинах блоков, но как можно увидеть из рис. 1.2, если длина блока является большой (как правило, более 5000), неравномерные LDPC коды превосходят турбо коды равной длины. С увеличением длины кодов улучшается вероятность ошибочного декодирования. LDPC коды длиной  могут быть надежно декодированы с помощью отношения
могут быть надежно декодированы с помощью отношения  отклонение от предела Шеннона может составлять менее 0,04 дБ [28].
отклонение от предела Шеннона может составлять менее 0,04 дБ [28]. , которая представляет собой разрыв в размере примерно 2,3 дБ от предела Шеннона при передаче по каналу связи с аддитивным гауссовским шумом. Этот интервал может быть уменьшен до 0,8-1,2 дБ.
, которая представляет собой разрыв в размере примерно 2,3 дБ от предела Шеннона при передаче по каналу связи с аддитивным гауссовским шумом. Этот интервал может быть уменьшен до 0,8-1,2 дБ. является бинарной переменной из алфавита {0,1}, а проверочный узел
является бинарной переменной из алфавита {0,1}, а проверочный узел  является ограничительным для соседних переменных узлов, т.е.
является ограничительным для соседних переменных узлов, т.е.
 есть множество всех «соседей»
есть множество всех «соседей»  - суммирование по модулю два.
- суммирование по модулю два. и размерности
и размерности  с равенством тогда и только тогда, когда все проверочные ограничения линейно независимы. Проверочной матрицей
с равенством тогда и только тогда, когда все проверочные ограничения линейно независимы. Проверочной матрицей  этого кода является матрица смежности графа
этого кода является матрица смежности графа  т. е.
т. е.  , входящие в
, входящие в 
 равно 1, тогда и только тогда, когда
равно 1, тогда и только тогда, когда  (
( -ый узел проверки) подключен к
-ый узел проверки) подключен к  (
( -ому переменному узлу).
-ому переменному узлу). , рассматривая множество ненулевых весов
, рассматривая множество ненулевых весов  для рёбер
для рёбер 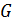 . Проверочная матрица в этом случае формируется с помощью множества весов. Другими словами
. Проверочная матрица в этом случае формируется с помощью множества весов. Другими словами  . В оставшейся части данной работы мы предполагаем, что коды – двоичные, если не указано иное.
. В оставшейся части данной работы мы предполагаем, что коды – двоичные, если не указано иное. имеет грань между левой вершиной
имеет грань между левой вершиной  и правой вершиной
и правой вершиной  очень мало. Как мы увидим позже, для LDPC кода с фиксированной скоростью
очень мало. Как мы увидим позже, для LDPC кода с фиксированной скоростью  дуг. Таким образом, с ростом
дуг. Таким образом, с ростом  уменьшается, что приводит к «редкому» коду.
уменьшается, что приводит к «редкому» коду. и степень проверочных узлов, как
и степень проверочных узлов, как  получим:
получим:

 . В ряде работ величина
. В ряде работ величина  называется кодируемой скоростью [12], но обычно возможная линейная зависимость между строками
называется кодируемой скоростью [12], но обычно возможная линейная зависимость между строками  проверочной степенью
проверочной степенью  и его проверочным распределением степеней дуг
и его проверочным распределением степеней дуг  , где
, где  обозначает долю дуг, падающую на переменные узлы степени
обозначает долю дуг, падающую на переменные узлы степени  обозначает долю дуг, падающую на проверочные узлы степени
обозначает долю дуг, падающую на проверочные узлы степени  и
и  с помощью их порождающих многочленов
с помощью их порождающих многочленов  и
и  . Оба варианта описаны в [17] и были использованы в литературе впоследствии. Обратите внимание, что граф характеризуется с точки зрения доли дуг каждой ступени, а не узлов каждой степени. Позже мы увидим, что это представление является более удобным. В оставшейся части данной работы под переменными (проверочными) степенями распределения мы будем иметь в виду переменные (проверочные) степени распределения дуг.
. Оба варианта описаны в [17] и были использованы в литературе впоследствии. Обратите внимание, что граф характеризуется с точки зрения доли дуг каждой ступени, а не узлов каждой степени. Позже мы увидим, что это представление является более удобным. В оставшейся части данной работы под переменными (проверочными) степенями распределения мы будем иметь в виду переменные (проверочные) степени распределения дуг. , легко заметить, что число переменных узлов
, легко заметить, что число переменных узлов 



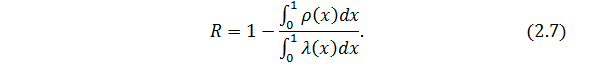
 которое является функцией соседнего переменного узла
которое является функцией соседнего переменного узла  имеет только два значения,
имеет только два значения,  . Когда сообщения являются условными PMF-функциями (probability mass functions – функции вероятностных мер),
. Когда сообщения являются условными PMF-функциями (probability mass functions – функции вероятностных мер),  , поэтому передача только одного из сообщений
, поэтому передача только одного из сообщений  эквивалентна передаче функции
эквивалентна передаче функции  . Равнозначно мы можем передавать комбинации
. Равнозначно мы можем передавать комбинации  . Последняя величина
. Последняя величина  или в случае PMF-функций
или в случае PMF-функций  известна, как отношение LLR (log likelihood ratio - логарифмическое правдоподобие) и наиболее распространенным типом сообщения, используемым в литературе. Причина заключается в том, что здесь методы корректировки просты и в компьютерной реализации это можно представить вероятностными значениями, которые очень близки к нулю или очень близки к единице, не вызывая ошибки в погрешности. Здесь мы только приводим методы корректировки, когда сообщения LLR. Для сообщений, взамен µ, мы используем m, чтобы различать общие методы передачи сообщений и методы передачи сообщений LLR. Методы корректировки для других видов сообщений можно найти в [29]. Обратите внимание, что сообщение уже не функция, а действительное число.
известна, как отношение LLR (log likelihood ratio - логарифмическое правдоподобие) и наиболее распространенным типом сообщения, используемым в литературе. Причина заключается в том, что здесь методы корректировки просты и в компьютерной реализации это можно представить вероятностными значениями, которые очень близки к нулю или очень близки к единице, не вызывая ошибки в погрешности. Здесь мы только приводим методы корректировки, когда сообщения LLR. Для сообщений, взамен µ, мы используем m, чтобы различать общие методы передачи сообщений и методы передачи сообщений LLR. Методы корректировки для других видов сообщений можно найти в [29]. Обратите внимание, что сообщение уже не функция, а действительное число. :
:
 представляет собой LLR сообщение, отправленное из узла
представляет собой LLR сообщение, отправленное из узла  в узел b, и
в узел b, и  представляет собой представляет собой совокупность всех соседних узлов
представляет собой представляет собой совокупность всех соседних узлов 
 является внутренним сообщением для переменного узла
является внутренним сообщением для переменного узла  . Здесь также изображено, что исходящие сообщения на дугу
. Здесь также изображено, что исходящие сообщения на дугу 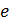 , соединенные с узлом
, соединенные с узлом  ), зависят от всех входящих сообщений на этот узел, кроме входящих сообщений на
), зависят от всех входящих сообщений на этот узел, кроме входящих сообщений на 
 , то обе
, то обе  и
и  имеют одинаковые вероятности и решение может быть осуществлено случайно.
имеют одинаковые вероятности и решение может быть осуществлено случайно. А также внутренние сообщения, которые влияют на исходящее сообщение на переменном узле
А также внутренние сообщения, которые влияют на исходящее сообщение на переменном узле 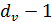 входящих сообщений и канального сообщения к
входящих сообщений и канального сообщения к  Те
Те  степени
степени  входящих сообщений к
входящих сообщений к  . Можно повторить эту процедуру для всех проверочных узлов, связанных с
. Можно повторить эту процедуру для всех проверочных узлов, связанных с  то до глубины
то до глубины  сообщения в дереве декодирования являются независимыми. Таким образом, независимое предположение верно до
сообщения в дереве декодирования являются независимыми. Таким образом, независимое предположение верно до 


