
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Другие алгоритмы декодированияСодержание книги Поиск на нашем сайте
В этом разделе мы представляем ряд важных алгоритмов передачи сообщений, которые по существу являются приближениями алгоритма sum-product. Здесь не показан полный перечень таких алгоритмов, но здесь охвачено большинство алгоритмов, которые будут использоваться в последующих главах этой работы. Алгоритм min-sum: В алгоритме min-sum метод корректировки на переменном узле такой же, как в алгоритме sum-product (2.9), но метод корректировки на проверочном узле
Обратите внимание, что Алгоритм А декодирования Галлагера: В этом алгоритме, введенном Галлагером [11], сообщение принадлежит алфавиту {0, 1}. Другими словами, используется не программная информация. Правило корректировки на проверочном узле
где ⨁ представляет сумму по модулю два двоичных сообщений. На переменном узле
где В оставшейся части этой работы мы ссылаемся на алгоритм А декодирования Галлагера. Алгоритм имеет худшее исполнение по сравнению с программными методами декодирования, введенными выше, но вычислительно гораздо менее сложный. Алгоритм Б декодирования Галлагера: Этот алгоритм также принадлежит Галлагеру и, подобно алгоритму А, все сообщения имеют двоичное значение. Единственная разница между этим алгоритмом и Алгоритм А это метод корректировки переменного узла. На переменном узле
где
где Мы докажем в главе 3, что алгоритм Б является наилучшим из возможных алгоритмов передачи двоичных сообщений равномерных LDPC кодов. Для неравномерных LDPC кодов, мы также покажем, что алгоритм Б самый оптимальный среди всех двоичных алгоритмов передачи сообщений, когда узлы в фактор графе кода не имеют информации об узловых степенях в их местном районе. В обоих алгоритмах А и Б, сообщения не несут программную информацию. Поэтому не удивительно, что вероятность ошибочного декодирования этих двух алгоритмов, по сравнению с алгоритмом sum-product, низкого качества. Но, конечно, они вычислительно гораздо дешевле. По мере того, как программа декодера (например, декодер sum-product) стремится по направлению сближения, величина сообщений становится очень большой, поэтому программная информация становится менее полезной. Мы используем эту особенность в главе 7, чтобы ускорить процесс декодирования, позволяя декодеру выбрать свой метод декодирования на каждой итерации, и мы увидим, что декодер стремится перейти на алгоритмы аппаратного декодирования в последующих итерациях.
LDPC коды: анализ
Прежде чем изучать методы анализа LDPC кодов, мы обсудим принцип итеративного декодирования, чтобы стала ясна цель такого анализа.
Рис. 2.4. Принцип итеративного декодирования. Итеративный декодер на каждой итерации использует два источника информации передаваемого кодового слова: информация из канала (внутренняя информация), а также информацию из предыдущей итерации (внешняя информация). От этих двух источников информации алгоритм декодирования пытается получить более качественную информацию о передаваемом кодовом слове, с помощью этих данных как внешней информации для следующей итерации (см. рис. 2.4). В успешном декодировании внешняя информация становится все лучше и лучше по мере того, как декодер производит итерацию. Таким образом, во всех методах анализа итеративного декодера статистика внешних сообщений на каждой итерации изучаема. Изучение эволюции PDF-функций из внешних сообщений, по очереди перебирая каждую итерацию, представляет собой наиболее полный анализ (известный как плотность эволюции). Однако, в качестве приближенного анализа можно проследить за эволюцией представителей этой плотности.
Анализ LDPC кодов Галлагера
В первоначальных работах Галлагера LDPC коды считались равномерными и декодирование предполагало использование двоичных сообщений (алгоритмы А и Б). Галлагер проводил анализ декодера в таких ситуациях [11]. Основной идеей его анализа является характеристика величины ошибок в сообщениях в каждой итерации с точки зрения ситуации в канале и величины ошибки в сообщениях в предыдущей итерации. Другими словами, при анализе Галлагера, эволюция величины ошибки в сообщениях изучаема, она также эквивалентна плотности эволюции, потому что PMF-функция двоичных сообщений является одномерной, т. е. она может быть описана одним параметром. Рис. 2.5. Дерево декодирования глубины один для равномерного (3, 6) LDPC кода. Анализ Галлагера базируется на предположении, что входящие сообщения на переменный (проверочный) узел являются независимыми. Хотя это предположение верно, только если граф без циклов, это доказано в [12], где ожидаемая вероятность ошибочного декодирования кода сводится к случаю без циклов по мере увеличения длины блока кода.
Дерево декодирования
Рассмотрим скорректированное сообщение от переменного узла Рис. 2.6. Дерево декодирования глубины два для неравномерного LDPC кода.
Обратите внимание, что, когда фактор граф является деревом, сообщения в дереве декодирования любой глубины независимы. Если фактор граф имеет циклы и его объем
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 387; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.54.210 (0.006 с.) |

 упрощается
упрощается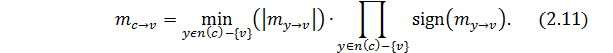
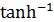 результата
результата  аппроксимируется как минимум абсолютного значения результирующего знака. Эта аппроксимация становится более точной величиной, когда величина сообщения увеличивается. Таким образом, в последующих итерациях, когда величина сообщения обычно большая, вероятность ошибочного декодирования этого алгоритма является почти такой же, как и алгоритма sum-product.
аппроксимируется как минимум абсолютного значения результирующего знака. Эта аппроксимация становится более точной величиной, когда величина сообщения увеличивается. Таким образом, в последующих итерациях, когда величина сообщения обычно большая, вероятность ошибочного декодирования этого алгоритма является почти такой же, как и алгоритма sum-product.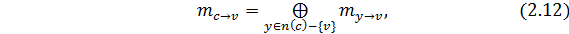
 , исходящее сообщение
, исходящее сообщение  такое же, как и внутреннее сообщение, если все внешние сообщения не согласны с внутренним сообщением. В этом случае исходящее сообщение такое же, как и внешние сообщения. Другими словами
такое же, как и внутреннее сообщение, если все внешние сообщения не согласны с внутренним сообщением. В этом случае исходящее сообщение такое же, как и внешние сообщения. Другими словами
 является внутренним двоичным сообщением и
является внутренним двоичным сообщением и 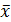 представляет собой дополнение к двоичной величине
представляет собой дополнение к двоичной величине 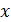 .
.
 целое число в диапазоне
целое число в диапазоне 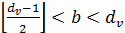 . Здесь, исходящее сообщение переменного узла такое же, как внутреннее сообщение, кроме
. Здесь, исходящее сообщение переменного узла такое же, как внутреннее сообщение, кроме  LDPC кода вычисляется по Галлагеру [11], и наименьшее число
LDPC кода вычисляется по Галлагеру [11], и наименьшее число 
 и
и 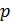 переходные вероятности канала (внутренняя величина ошибки в сообщении) и внешняя величина ошибки в сообщении, соответственно. С этого момента, мы будем ссылаться на алгоритм Галлагера Б как на алгоритм Б.
переходные вероятности канала (внутренняя величина ошибки в сообщении) и внешняя величина ошибки в сообщении, соответственно. С этого момента, мы будем ссылаться на алгоритм Галлагера Б как на алгоритм Б. для проверки узла в декодере. Это сообщение вычисляется из
для проверки узла в декодере. Это сообщение вычисляется из 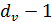 входящих сообщений и канального сообщения к
входящих сообщений и канального сообщения к  Те
Те  . Исходящее сообщение этого проверочного узла рассчитывается из
. Исходящее сообщение этого проверочного узла рассчитывается из  входящих сообщений к
входящих сообщений к  . Можно повторить эту процедуру для всех проверочных узлов, связанных с
. Можно повторить эту процедуру для всех проверочных узлов, связанных с  то до глубины
то до глубины  сообщения в дереве декодирования являются независимыми. Таким образом, независимое предположение верно до
сообщения в дереве декодирования являются независимыми. Таким образом, независимое предположение верно до 


