Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множество внешней устойчивости графаСодержание книги
Поиск на нашем сайте
Множество внешней устойчивости – множество вершин, для которых выполняется одно из следующих правил: 1). Любая вершина входит в это множество 2) Либо вершина не входит в это множество, но из этой вершины есть дуга в данное множество. Пусть дан граф
Число внешней устойчивости (β) – это наименьшая мощность из всех множеств внешней устойчивости.
Алгоритм Магу для определения множества внешней устойчивости. Пусть дан граф Вводятся булевые переменные Тогда определение множества внешней устойчивости (3.12) запишется следующим образом:
Для
Данное уравнение лежит в основе алгоритма Магу Алгоритм Магу состоит из следующих этапов: 1. Для графа составляется матрица смежности 2. Матрица смежности дополняется единицами (1) по главной диагонали. 3. Для каждой строки выписываются дизъюнкции. 4. Выражение приводится к ДНФ. 5. Все вершины, входящие в элементарную конъюнкцию, образуют множество внешней устойчивости
ПРИМЕР Определить множество внешней устойчивости для графа, представленного на рис. 3.7. Матрица смежности имеет вид:
Дополним матрицу смежности единицами по главной диагонали
Для каждой строки выписываются дизъюнкции:
Приведем выражение к ДНФ:
Множества внутренней устойчивости:
Числом внешней устойчивости
Ядром графа называется подмножество вершин, являющихся одновременно внутренней и внешней устойчивостью. Граф, представленный на рис. 3.7. имеет ядро
Множество путей в графе
По матрице смежности можно определить, сколько различных путей существует между i -той и j - той вершинами длиной в к единиц. Для этого необходимо определить матрицу Если элемент
Если
А лгоритм фронта волны. Поиск минимального пути в графе.
Одной из самых распространенных задач в теории графов является задача поиска минимального пути в графе. Рассмотрим некоторые свойства минимальных путей 1. Любой минимальный путь является простым путем. 2. Если путь Пусть Г-1х – прообраз вершины xi – это множество вершин, из которых исходят дуги в вершину xi. Одним из алгоритмов поиска минимального пути в графе является алгоритм фронта волны (FW –Front Wave)
Алгоритм фронта волны.
Пусть необходимо найти минимальный путь из вершины 1. Выписываются все вершины с 1 по n. Вершина 2. Находится первый фронт волны
3. Все вершины, принадлежащие первому фронту волны, помечаются индексом 1. 4. Вводится счетчик шагов (фронтов волны) 5. Если 6. Если
7. Находятся промежуточные вершины
где 8. Определяется
ПРИМЕР Пусть задан граф матрицей смежности:
Необходимо найти минимальный путь из вершины 1. Выпишем все вершины. Вершина
2. Находится первый фронт волны:
3. Все вершины, принадлежащие первому фронту волны, помечаются индексом «1». 0 1 1
4. Так как
5. Все вершины, принадлежащие второму фронту волны, помечаются индексом «2». 0 2 2 1 1
6. Так как
7. Так как
8. Находятся промежуточные вершины
Выберем
Выберем Таким образом, минимальный путь из вершины
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1169; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.211.55 (0.009 с.) |

 . Тогда для множества внешней устойчивости
. Тогда для множества внешней устойчивости  справедливо следующее:
справедливо следующее: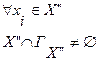 (3.12)
(3.12) .
. и
и 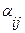 по тому же правилу, что и для алгоритма Магу для определения множества внутренней устойчивости.
по тому же правилу, что и для алгоритма Магу для определения множества внутренней устойчивости. (3.13)
(3.13) справедливо следующее
справедливо следующее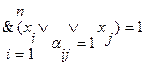 (3.14)
(3.14)

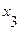

 (3.15)
(3.15)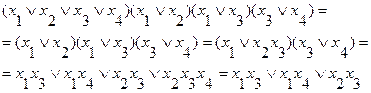 (3.16)
(3.16)
 = 2.
= 2.
 , где
, где 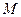 - матрица смежности.
- матрица смежности. матрицы
матрицы  - между i -той и j - той вершины не существует пути длиной в к единиц;
- между i -той и j - той вершины не существует пути длиной в к единиц; - между i -той и j - той вершины существуют
- между i -той и j - той вершины существуют  различных путей длиной в к единиц;
различных путей длиной в к единиц; - минимальный, то любые пути
- минимальный, то любые пути  внутри минимального пути также будут минимальны.
внутри минимального пути также будут минимальны. .
. помечается индексом 0.
помечается индексом 0.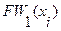 как множество вершин образа вершины
как множество вершин образа вершины 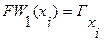 (3.17)
(3.17) .
. или
или 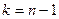 , то вершина
, то вершина  , то переходим к пункту 8. В противном случае существует путь из вершины
, то переходим к пункту 8. В противном случае существует путь из вершины 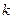 единиц, и этот путь минимальный:
единиц, и этот путь минимальный:
 z по правилу:
z по правилу:
 , (3.18)
, (3.18) - прообраз вершины
- прообраз вершины 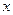 - множество вершин, из которых заходят дуги в вершину
- множество вершин, из которых заходят дуги в вершину  фронт волны как все непомеченные вершины, принадлежащие образу вершин
фронт волны как все непомеченные вершины, принадлежащие образу вершин 



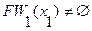 ,
,  и
и  , то определяем второй фронт волны:
, то определяем второй фронт волны:
 ,
,  и
и  , то определяем третий фронт волны:
, то определяем третий фронт волны:
 , то существует путь из вершины
, то существует путь из вершины 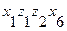
 :
: