
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Минимизация сложных высказываний.Содержание книги
Поиск на нашем сайте Существует несколько способов минимизации сложных высказываний. Рассмотрим самые распространенные: · метод Квайна; · карты Вейча; · минимизирующие карты.
Метод Квайна.
Алгоритм метода Квайна включает в себя следующие этапы: 1. Любая формула 2. СДНФ приводится к сокращенной ДНФ (СкДНФ). При получении СкДНФ используются следующие формулы равносильности: а) Формула склеивания
б) Формула неполного склеивания
в) Формула поглощения
Применяя все возможные процедуры склеивания, СДНФ приводится к СкДНФ. 3. Минимальная форма формулы
ПРИМЕР. Необходимо найти МДНФ формулы:
1 2 3 4 5 6 Осуществляем всевозможные склеивания 1-2 1-4 2-3 3-6 4-5 5-6 СкДНФ имеет вид:
Составляем импликантную матрицу
По данной импликантной матрице можно выбрать следующие МДНФ
Метод минимизирующих карт. Алгоритм метода минимизирующих карт включает в себя следующие этапы: 1. Любая формула приводится к СДНФ. 2. Составляется таблица всевозможных сочетаний переменных. 3. Из таблицы вычеркиваются те строки, которые не содержат конституенты СДНФ. Конъюнкции этих строк вычеркиваются в других строках. 4. В каждой строке оставляются конъюнкции с минимальным количеством переменных. 5. Из каждой строки выбирается олна конъюнкция и составляется ДНФ. 6. Из построенных ДНФ выбирается минимальная.
ПРИМЕР
Дана СДНФ
* - помечены строки, не содержащие конституенты СДНФ. После соответствующих преобразований получаем следующую таблицу
После всевозможного перебора остаются следующие МДНФ:
Метод минимизации с помощью карт Вейча.
Алгоритм метода карт Вейча включает в себя следующие этапы: 1. Любая формула приводится к СДНФ. 2. Составляется карта Вейча. Карта Вейча – это таблица всех возможных комбинаций значений переменных. В соответствующие ячейки заносятся единицы, соответствующие конституентам СДНФ. 3. Единицы, стоящие по вертикали и горизонтали, объединяются (по 2, по 4. по 8 и т.д.). Объединение единиц соответствует операциям склеивания и поглощения. Иначе говоря, формируются максимальные подкубы. 4. Для каждого объединения выписываются конъюнкции из элементов, общих для каждой единицы, входящих в объединение.. 5. Выше полученные конъюнкции составляют МДНФ.
Карты Вейча удобны при поиске МДНФ функций двух, трех и четырех переменных. n=2 СДНФ=
МДНФ=
n=3 СДНФ=
МДНФ= n=4
СДНФ=
МДНФ=
Булевые функции и их свойства.
Булевой функцией называется функция n переменных, которая принимает значение 1 или 0, а так же ее аргументы тоже принимают значение 1 или 0. Булевая функция имеет следующие свойства: 1. Свойство сохранения нуля 2. Свойство сохранения единицы
ПРИМЕР Логическая операция – дизъюнкция
3. Линейность
где ПРИМЕР
Эквивалентность является линейной функцией:
4. Монотонность
5. Самодвойственность Двойственной функцией называется функция:
Тогда свойство самодвойственности может представлено:
ПРИМЕР
Отрицание является самодвойственной функцией:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 462; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 приводится к СДНФ.
приводится к СДНФ.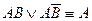




















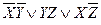






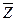






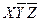
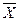








 1
1


 1
1




 1
1
 1
1



 . Булевая функция сохраняет нуль, если функция при нулевых значениях аргумента принимает значение нуль.
. Булевая функция сохраняет нуль, если функция при нулевых значениях аргумента принимает значение нуль. . Булевая функция сохраняет единицу, если функция при единичных значениях аргумента принимает значение единица.
. Булевая функция сохраняет единицу, если функция при единичных значениях аргумента принимает значение единица. обладает и свойством сохранения нуля (
обладает и свойством сохранения нуля ( ), и свойством сохранения единицы (
), и свойством сохранения единицы ( )
) . Функция является линейной, если её можно представить в виде:
. Функция является линейной, если её можно представить в виде:
 - булевая переменная
- булевая переменная
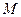 . Функция является монотонной, если для любых произвольных наборов a и b выполняются следующие неравенства:
. Функция является монотонной, если для любых произвольных наборов a и b выполняются следующие неравенства:
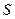 . Функция называется самодвойственной, если она равна двойственной ей функции.
. Функция называется самодвойственной, если она равна двойственной ей функции.





