
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямое (декартовое) произведение множество.Содержание книги
Поиск на нашем сайте Прямым (декартовым) произведением множества
ПРИМЕР. Пусть заданы
Рис. 8 График прямого произведения множеств
Пусть заданы
Соответствия.
Соответствием называется тройка вида
ПРИМЕР.
Дано соответствие <P,X,Y> такое, что: X={x| x ³ 2}; Y={y| y ³ 5}; P={<x,y>| y=x2}.
Рис. 9 График соответствия.
Если Если
Свойства соответствий.
1. Соответствие называется функциональным, если его график функционален. 2. Соответствие называется инъективным, если его график инъективен. 3. Соответствие называется всюду определенным, если проекция его графика на первую ось совпадает с областью отправления. Пр P1=X. 4. Соответствие называется сюръективным, если проекция его графика на вторую ось совпадает с областью прибытия. Пр P2=Y. 5. Соответствие называется биективным (взаимнооднозначным), если оно функционально, инъективно, всюду определенно, сюръективно.
ПРИМЕР.
Данное соответствие 1. функциональное, так как две и более конфет не может быть упаковано в один фантик; 2. инъективное, так как одна конфета не может быть завернута в два антика одновременно (брак упаковочной техники не рассматривается); 3. не всюду определенное, так как существуют сорта конфет, которые продаются без фантиков (зефир, мармелад); 4. сюръективное, так как фантики без конфет - это мусор; 5. не биективное, так как является несюръективным соответствием.
Отношения.
Отношением называется пара вида
ПРИМЕР.
Пусть дано j=<F,N>, где F={<2,1>;<3,1>;<3,2>;¼<4,1>;<4,2>;¼} Отношение называется полным, если F=M2. Отношение называется отношением равенства, если F=DM={<x,x>;<y,y>;¼}. Отношение называется отношением неравенства, если F=M2\DM. Запись xjy означает, что между x и y существует отношение j.
Пусть даны два отношения j=<F,M> и r=<R,M>. Над данными отношениями могут быть выполнены следующие операции: 1. объединение j 2. пересечение j 3. дополнение 4. разность j\r=<Ф\R,M>. 5. композиция j 6. инверсия j-1=<Ф-1,M>.
Основные свойства отношений. 1. Рефлексивность. Отношение называется рефлексивным, если для всех x выполняется условие: xjx или DMÍF. Антирефлексивность. Отношение называется антирефлексивным, если для всех x выполняется условие: ùxjx (символ “ ù“ означает “не выполняется”) или 3. Симметричность. Отношение называется симметричным, если для всех x выполняется условие: xjy Þ yjx или Ф=Ф-1. Антисимметричность. Отношение называется антисимметричным, если для всех x выполняется условие: xjy и x¹y Þù yjx или Асимметричность. Отношение называется асимметричным, если для всех x выполняется условие: xjy Þù yjx или 6. Связность (полнота). Отношение называется связным (полным), если для всех x выполняется условие: x¹y Þ xjy или yjx или М2\DMÍ Транзитивность. Отношение называется транзитивным, если для всех x выполняется условие: xjy и yjz Þ xjz или Ф
ПРИМЕР
Какими свойствами обладает отношение j=<Ф,X>, где X={1; 2; а}, Ф={<1,1>;<a,a>;<a,2>;<2,2>}. Определим Ф-1, DX: Ф-1={<1,1>;<a,a>;<2,a>;<2,2>} DX={<1,1>;<2,2>;<a,a>}. Отношение является: - рефлексивным, так как DXÍФ; - антисимметричным, так как - транзитивным, так как Ф - несвязное, так как X2\DX={<1,2>;<1,a>;<2,1>;<2,a>;<a,1>;<a,2>}Ë Ф Отношение называется отношением эквивалентности, если оно рефлексивное, симметричное и транзитивное. Отношение называется отношением нестрогого (частичного) порядка ( Отношение называется совершенно нестрого порядка ( Отношение называется строго порядка ( Отношение называется совершенно строго порядка ( Решетки. Диаграммы Хассе. Рассмотрим отношение частичного порядка: “быть подмножеством“ на множестве-степени М={1,2}. j=<F,M>, где Ф={<{Æ},{Æ}>;<{Æ},{1}>;<{Æ},{2}>;<{Æ},{1,2}>;<{1},{1}>;<{1},{1,2}>;<{2},{2}>;<{2},{1,2}>};<{1,2},{1,2}>}. Графически данное отношение можно изобразить следующим образом:
РИС 10 Графическое изображения отношения Отношение является рефлексивным (графически это отображается петлями), антисимметричным (графически - однонаправленные стрелки), транзитивным (графически - транзитивными замыканиями вида: Для отношений частичного порядка применимы диаграммы Хассе, которые строятся на основе обыкновенной диаграммы следующим образом: 1. рефлексивные петли и транзитивные связи не изображаются; 2. большие элементы (элементы, в которые входят стрелки) располагают выше.
Таким образом, диаграмма Хассе для вышеприведенного примера будет выглядеть следующим образом:
РИС 11 Диаграмма Хассе
Для частично упорядоченного множества справедливо следующее: 1. Элемент аÎА называется наибольшим (наименьшим), если для всех хÎ А выполняется x 2. Элемент аÎА называется максимальным (минимальным), если нет а множестве А элементов, больших (меньших), чем а. Максимальных (минимальных) элементов может быть несколько. 3. Пусть ВÍА. Элемент аÎА называется можарантой (минорантой), если для всех х Î В этот элемент является наибольшим (наименьшим). 4. Множество мажорант В образует верхнюю границу множества В. Множество минорант В образует нижнюю границу множества В. 5. Наименьший элемент верхней границы называется точной верхней границей, или supremum (sup) B. Наибольший элемент нижней границы называется точной нижней границей, или infimum (inf) B. 6. Частично упорядоченное множество, у которого для любой пары элементов определен и существует sup и inf, называется решеткой.
ПРИМЕР Пусть дано отношение, представленное на диаграмме Хассе
РИС 12 Диаграмма Хассе
Отношение А не является решеткой, т.к. элементы 7 и 8 не имеют sup. Отношение В является решеткой, т.к. любая пара имеет sup и inf.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 537; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.006 с.) |

 и множества
и множества 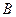 называется множество пар таких, что:
называется множество пар таких, что: , (29)
, (29) и
и  :
: 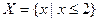 ,
, 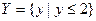 . Тогда прямое (декартовое) произведение этих множеств может быть представлено графически:X={x | x£2}
. Тогда прямое (декартовое) произведение этих множеств может быть представлено графически:X={x | x£2}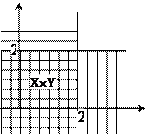
 ,
, 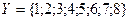 . Тогда прямое (декартовое) произведение этих множеств представляет шахматную доску.
. Тогда прямое (декартовое) произведение этих множеств представляет шахматную доску.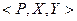 . При этом
. При этом  - график соответствия.
- график соответствия.
 , то данное соответствие называется полным.
, то данное соответствие называется полным. , то данное соответствие называется пустым.
, то данное соответствие называется пустым.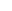 Дано соответствие <P,X,Y>, где X - множество конфет, Y - множество фантиков, P - ”быть упакованным в фантик”. Какими свойствами обладает данное соответствие?
Дано соответствие <P,X,Y>, где X - множество конфет, Y - множество фантиков, P - ”быть упакованным в фантик”. Какими свойствами обладает данное соответствие? такая, что ФÍM2 (M2=M
такая, что ФÍM2 (M2=M  M), где Ф - график отношения, М - это множество, между элементами которого существует данное отношение.
M), где Ф - график отношения, М - это множество, между элементами которого существует данное отношение. , а график отношения определяется как
, а график отношения определяется как 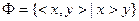 . Это отношение ”X больше Y” на множестве натуральных чисел. Данное отношение задано описанием свойств. Перечислением данное отношение может быть задано следующим образом:
. Это отношение ”X больше Y” на множестве натуральных чисел. Данное отношение задано описанием свойств. Перечислением данное отношение может быть задано следующим образом:

 Операции над отношениями.
Операции над отношениями.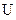 r=<F
r=<F  r=<Ф
r=<Ф  `
` r=<Ф
r=<Ф 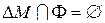 .
. ÍDM.
ÍDM. .
. ÍDX;
ÍDX; ), если оно рефлексивное, антисимметричное и транзитивное.
), если оно рефлексивное, антисимметричное и транзитивное. ),если оно рефлексивное, антисимметричное, транзитивное и связное.
),если оно рефлексивное, антисимметричное, транзитивное и связное. ), если оно антирефлексивное, антисимметричное и транзитивное.
), если оно антирефлексивное, антисимметричное и транзитивное.





