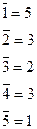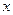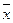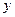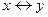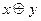Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгебраическое представление решеток.Содержание книги
Поиск на нашем сайте
Введем обозначения: sup(a,b)=a 1. Коммутативный: a 2. Ассоциативный: а 3. Идемпотентности: а 4. Поглощения: а Решетки, для которой выполняется дистрибутивный закон: а называется дистрибутивной решеткой. Решетка называется ограниченной, если он имеет максимальный и минимальный элемент.
ПРИМЕР
РИС 13 Диаграмма Хассе решетки
Решетка не является дистрибутивной, т.к. для элементов {2;3;4} не выполняется дистрибутивный закон:
Дана решетка j=<F,M>, где М={x½0<x<1}, Ф={<x,y>½x<y}. Эта решетка не является, так как не определен максимальный элемент (0.9999999999....) и минимальный элемент (0.0000000...1).
Обозначим в ограниченной решетке максимальный элемент 1, а минимальный элемент 0. Элемент
ПРИМЕР Рассмотрим решетку, представленную на рис. 13. Найдем дополнения для каждого элемента решетки
Данная решетка является решеткой с дополнением.
Ограниченная дистрибутивная решетка с дополнением называется булевой решеткой.
На рис. 14 представлены дистрибутивные решетки
РИС. 14. Примеры булевых решеток
Математическая логика Высказывания и операции над высказываниями.
Высказыванием называется повествовательное предложение, о котором можно сказать истинно оно или ложно. 1. Москва - столица России. 2. Если студент учится на отлично, то он получит красный диплом. 3. Осадки - это снег или дождь. 4. Курица – не птица. 5. Пейте томатный сок. 6. Я лгу. 7. 23<5 Высказываниями являются 1, 2, 3,4 и 7 предложения. Предложение 5 не является высказыванием, так как про него нельзя сказать истинно оно или ложно. Предложение 6 является логическим парадоксом. Элементарным высказыванием называется высказывание, которое содержит одно утверждение (предложения 1,7). Сложное (составное) высказывание состоит из элементарных высказываний связанных с помощью следующих предлогов и частиц: И, НЕ, ИЛИ, ЕСЛИ - ТО, ТОГДА И ТОЛЬКО ТОГДА и другие. Предложения 2,3,4 являются сложными высказываниями.
Операции над высказываниями. Отрицанием высказывани я х называется новое высказывание, которое истинно, если высказывание ложное и наоборот. Таблица истинности операции отрицания имеет вид:
Дизъюнкцией двух высказываний x и y(логическое «или») называется новое высказывание, которое будет истинным тогда когда, когда хотя бы одно из высказываний будет истинным.
Конъюнкцией двух высказываний x и y(логическое «и») называется новое высказывание, которое будет истинным тогда когда, когда оба высказывания истины. Обозначение операции конъюнкция - & (
Импликацией двух высказываний x и y(«если – то») называется новое высказывание, которое ложно тогда, когда х(предпосылка) - истинно, а у(следствие) - ложно.
Эквивалентностью двух высказываний x и y(«тогда и только тогда») называется новое высказывание, которое будет истинно, если высказывания х и у будут одновременно истинны или ложны.
Неодназночностью (суммой по модулю два) двух высказываний x и y(«тогда и только тогда») называется новое высказывание, которое будет истинно тогда когда одно из высказываний х или у истинно, а другое ложно.
Штрих Шеффера (логическое «и - не») высказываний x и y - это новое высказывание, которое будет ложно тогда и только тогда когда оба высказывания истинны.
Стрелка Пирса (логическое «или - не») высказываний x и y - это новое высказывание, которое будет истинно тогда и только тогда когда оба высказывания ложны.
Для операций справедливы следующие приоритеты: ù, &, Ú, ®, «.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 421; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.42.13 (0.01 с.) |

 b, inf(a,b)=a
b, inf(a,b)=a 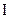 b. Для решетки справедливы следующие свойства:
b. Для решетки справедливы следующие свойства: (в
(в  в)=а а
в)=а а 

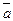 называется дополнением элемента а в данной решетке, если
называется дополнением элемента а в данной решетке, если 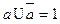 и
и 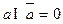 . Решетка называется с дополнением, если каждый элемент имеет хотя бы одно дополнение.
. Решетка называется с дополнением, если каждый элемент имеет хотя бы одно дополнение.