Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ярусно-параллельная форма графовСодержание книги
Поиск на нашем сайте
Граф, не имеющий контуров, может быть представлен в ярусно-параллельной форме. Ярусно-параллельная форма – это такой вид графа, у которого в верхний нулевой ярус помещены вершины, имеющие только исходящие дуги; в нижний ярус помещены вершины, имеющие только входящие дуги. На k -том ярусе помещены вершины, которые имеют входящие дуги из предыдущих ярусов, среди которых хотя бы одна дуга из (k-1)- того яруса. Количество вершин в ярусе определяет ширину яруса. Наибольшая ширина яруса определяет ширину графа в ярусно-параллельной форме. Количество ярусов определяет высоту графа в ярусно-параллельной форме.
Алгоритм приведения графа к ярусно-параллельной форме. 1. Составляется матрица смежности графа. 2. Матрица смежности просматривается в поисках нулевых столбцов. Вершины, которым соответствуют нулевые столбцы, помещаются в нулевой ярус. 3. Из матрицы смежности столбцы и строки, соответствующие вершинам нулевого яруса. 4. Повторяется п.2 данного алгоритма до тех пор, пока не будут охвачены все вершины. 5. По исходной матрице смежности восстанавливаются дуги между вершинами.
ПРИМЕР Привести граф к ярусно-параллельной форме.
Рис. 3.8 Граф
1. Матрица смежности имеет вид:
2. В нулевой ярус помещаются вершины 3 и 8. 3. Из матрицы смежности вычеркиваются строки и столбцы, соответствующие вершинам 3 и 8:
4. В первый ярус помещаются вершины 4 и 5. 5. Из матрицы смежности вычеркиваются строки и столбцы, соответствующие вершинам 4 и 5:
6. Во второй ярус помещается вершина 1. 7. Из матрицы смежности вычеркиваются строка и столбец, соответствующие вершине 1:
8. В третий (последний) ярус помещаются вершины 2,6 и 7. Таким образом, граф может быть представлен в ярусно-параллельной форме:
Рис. 3.9 Граф
Высота графа - 4 яруса; ширина -3.
Деревья и леса Отделенными называются вершины, для которых не существует соединяющего эти вершины пути. Неотделенными называются вершины, между которыми существует путь. Подграфом графа
Компонентой связности называется подграф, порождаемый множество неотделенных вершин.
ПРИМЕР
На рис. 3.10 представлен граф, имеющий две компоненты связности {1,2,3,4} и {5.6}
Рис. 3.10 Граф
Связанным графом называется граф, имеющий одну компоненту связности. Дерево – связный неориентированный граф, в котором отсутствует цикл. На рис. 3.11 представлены графы- деревья.
Рис. 3.11 Граф Лесом называетсяграф, имеющий несколько компонентов связности, причем каждая из компонент является деревом. Цикломатическим числом (g) графа называется минимальное количество ребер, которое необходимо изъять из графа, чтобы он стал деревом. Цикломатическое число определяется по формуле:
где N – количество ребер, k – количество вершин.
Алгоритм получения дерева из графа
1. Выбирается любая вершина. Счетчик i принимаем равным 1 (i=1). 2. Если i = k, то дерево построено. 3. Если i ¹ k, то выбирается любая незадействованная вершина и ребро, соединяющее данную вершину с любой из выбранных. 4. Счетчик увеличивается на единицу.(i= i+1). 5. Переход на пункт 2.
ПРИМЕР Преобразовать граф, представленный на рис. 3.12 в дерево:
Рис. 3.12
1. Найдем цикломатическое число 2. Выбираем вершину 5. 3. Присоединяем вершину 3. 4. 5. Присоединяем вершину 4. 6. 7. Присоединяем вершину 1. 8. 9. Присоединяем вершину 2. 10. 11. Все вершины охвачены. Дерево построено
Рис. 3.13 ТЕОРИЯ АЛГОРИТМОВ Алгоритм – это точное, понятное предписание о том, какие действия и в каком порядке должны быть выполнены, чтобы решить любую задачу из класса однотипных задач. Алгоритм обладает следующими характеристиками: 1. Дискретность. Алгоритм – это процесс последовательного построения величин таким образом, что в начальный момент задается исходная конечная система величин, а в каждый следующий момент система величин получается по определенному закону из системы, имевшихся в предыдущий момент времени. 2. Детерминированность. Система величин, получаемых в какой-то не начальный момент, однозначно определяется системой величин, полученных в предшествующие моменты времени. 3. Элементарность шагов алгоритмов. Закон получения последующей системы величин из предшествующих должен быть простым. 4. Массовость алгоритма. Начальная система величин может выбираться из некоторых потенциально бесконечного множества. Иначе говоря, алгоритм должен обеспечивать решение некоторому множеству (классу) задач с различными параметрами(коэффициентами). 5. Результативность алгоритма. Последовательный процесс построения величин должен быть конечным и давать результат, того есть решение задачи. Основная задача теории алгоритмов – это решение проблемы алгоритмическойразрешимости, а не поиск правила (способа/метода) ее решения. Теория алгоритмов дает ответ на вопрос «Данная задача имеет решение?», и не отвечает на вопрос «Как решается данная задача?» В рамках такого подхода к определению понятия алгоритма можно определить три основных направления: 1. Первое направление связано с уточнением понятия эффективно вычисляемой функции. В результате был выделен класс так называемых рекурсивных функций. 2. Второе направление связано с машинной математикой. Здесь сущность понятия алгоритма раскрывается путем рассмотрения процессов, осуществляемых в машине. Впервые это было сделано Тьюрингом, который предложил общую и вместе с тем самую простую концепцию вычислительной машины. Ее описание было дано Тьюрингом в 1937 г. А это направление в теории алгоритмов получило название - машина Тьюринга. 3. Третье направление связано с понятием нормальных алгоритмов, введенным и разработанным российским математиком А. А. Марковым. х Нормальные алгоритмы Маркова. Это направление получило название нормальные алгоритмы Маркова.
Рекурсивная функция Основные понятия: элементарные функции, правила образования новых функций. Простейшие функции: 1. Функция сохранения нуля (нуль-функция)
2. Функция сдвига
3. Функция-проекция
Правила преобразования функций
1. Правило подстановки (суперпозиции) Пусть даны функции:
где g и h являются или простейшими, или выведенными из простейших. Правило вывода (4.4) означает, что функция
ПРИМЕР Функция
2. Правило примитивной рекурсии Основывается на простейших или выведенных из простейших функциях g и h: Пусть
Тогда новая функция
Следует отметить, что функция
ПРИМЕР
Пусть некоторая функция
Нетрудно заметить, что функция Вычислим значение функции
Нетрудно заметить, что функция 3. m - оператор (оператор нахождения наименьшего корня у) Оператор
(Читается: «наименьшее
Для вычисления функции 1. Вычисляется 2. Вычисляется Если окажется, что для всех
ПРИМЕР Дана функция
Таким образом,
Функция Функция Функция называется общерекурсивно й, если она частично рекурсивная и всюдуопределенная.
Тезис А. Черча. Если функция является общерекурсивной, то она выполнима, т.е. имеет алгоритм решения.
Машина Тьюринга Если для решения некоторой массовой проблемы известен алгоритм, то для его реализации необходимо лишь четкое выполнение предписаний этого алгоритма. Автоматизм, необходимый при реализации алгоритма, приводит к мысли о передаче функции человека, реализующий алгоритм, машине. Идею такой машины предложил в 1937 году английский математик А. Тьюринг. Машина Тьюринга включает в себя: 1. Внешний алфавит - конечное множество символов 2. Внутренний алфавит - конечное множество символов
3. Операторы перемещения Т={Л, П, Н}. Л, П, Н – это символы сдвига «влево», «вправо» и «на месте». 4. Бесконечная лента Бесконечная лента характеризует память машины. Она разбита на клеточки. В каждую клеточку может быть записан только один символ из внешнего алфавита. 5. Управляющая головка. Управляющая головка (УГ) передвигается вдоль ленты и может останавливаться напротив какой-либо клетки, т. е. считывать символ 6. Управляющая головка. Управляющая головка (УГ) передвигается вдоль ленты и может останавливаться напротив какой-либо клетки, т. е. считывать символ.
Рис. 4.1. Функциональная схема машины Тьюринга.
7. Программа машины Тьюринга (Р) - совокупность всех команд, Программа представляется в виде таблицы и называется Тьюринговой функциональной схемой.
Таким образом, машина Тьюринга может быть представлена в виде четверки:
Работа машины Тьюринга: Информация, хранящаяся на ленте, является набором символов из внешнего алфавита. Начальное состояние управляющей головки характеризуется символом внутреннего алфавита
Если в результате операции машина перейдет в состояние
ПРИМЕР Построить машину Тьюринга, которая будет стирать последнюю единицу в последовательности единиц. Внешний алфавит -
Проверим работоспособность машины Тьюринга: 1. 2. 3. 4. 5. Тезис А. Черча. Если функция выполнима, то она всегда может быть представлена в виде машины Тьюринга.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 931; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.147.225 (0.011 с.) |



 называется граф вида:
называется граф вида: (3.19)
(3.19)


 , (3.20)
, (3.20)
 , т.е. необходимо изъять 4 ребра.
, т.е. необходимо изъять 4 ребра.





 (4.1)
(4.1)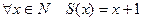 (4.2)
(4.2) (4.3)
(4.3) Тогда
Тогда (4.4)
(4.4) получена из функций
получена из функций  правилом суперпозиции
правилом суперпозиции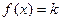 может быть получена путем применения
может быть получена путем применения 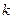 раз правила суперпозиции на основе функций
раз правила суперпозиции на основе функций 
 , (4.5)
, (4.5)
 может быть выведена по правилу:
может быть выведена по правилу: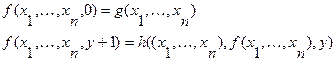 (4.6)
(4.6) зависит от
зависит от  аргументов, функция
аргументов, функция  аргументов, функция
аргументов, функция 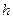 зависит от
зависит от  аргументов. Иначе говоря, правило примитивной рекурсии позволяет получить n + 1 -местную функцию из n -местной и n + 2 - местной функций.
аргументов. Иначе говоря, правило примитивной рекурсии позволяет получить n + 1 -местную функцию из n -местной и n + 2 - местной функций. задана правилом рекурсии
задана правилом рекурсии
 , функция
, функция 
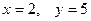 .
.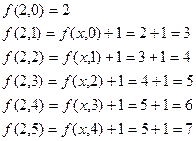
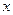 и
и 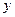 .
. определяет наименьшее значение у, при котором
определяет наименьшее значение у, при котором 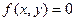 при фиксированном значении. Принято обозначение
при фиксированном значении. Принято обозначение (4.7)
(4.7) (4.8)
(4.8) существует следующий алгоритм:
существует следующий алгоритм: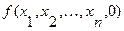 . Если это значение функции
. Если это значение функции  . Если
. Если  , то осуществляется переход к следующему шагу.
, то осуществляется переход к следующему шагу. . Если это значение функции
. Если это значение функции  . Если
. Если  , то осуществляется переход к следующему шагу. И т. д.
, то осуществляется переход к следующему шагу. И т. д. , то функция
, то функция  считается неопределенной.
считается неопределенной. . Необходимо определить
. Необходимо определить 


 называется частично рекурсивной, если она получена из простейших функций за конечное число шагов на основе правил подстановки, примитивной рекурсии или m - оператора.
называется частично рекурсивной, если она получена из простейших функций за конечное число шагов на основе правил подстановки, примитивной рекурсии или m - оператора. . В этом алфавите в виде слова кодируется та информация, которая подается в машину. Машина перерабатывает информацию, поданную в виде слова, в новое слово. Обычно символ Внешний алфавит - конечное множество символов
. В этом алфавите в виде слова кодируется та информация, которая подается в машину. Машина перерабатывает информацию, поданную в виде слова, в новое слово. Обычно символ Внешний алфавит - конечное множество символов 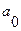 обозначает пробел.
обозначает пробел. . Для любой машины число состояний фиксировано. Два состояния имеют особое назначение
. Для любой машины число состояний фиксировано. Два состояния имеют особое назначение  - начальное состояние машины,
- начальное состояние машины,  - заключительное состояние (стоп-состояние).
- заключительное состояние (стоп-состояние).
 (4.9)
(4.9) , считывает входной символ
, считывает входной символ  и по таблице работы совершает операцию сдвига
и по таблице работы совершает операцию сдвига  , переходя в состояние
, переходя в состояние  , при этом входное слово
, при этом входное слово 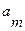 :
:
 . Внутренний алфавит -
. Внутренний алфавит -  , при этом состояние
, при этом состояние 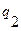 - стирание последней единицы. При этом следует заметить, что ситуация
- стирание последней единицы. При этом следует заметить, что ситуация  в работе машины Тьюринга невозможна, поэтому соответствующая клеточка доопределена произвольно, например
в работе машины Тьюринга невозможна, поэтому соответствующая клеточка доопределена произвольно, например  . Начальное состояние
. Начальное состояние