
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равносильные формулы логики предикатов.Содержание книги
Поиск на нашем сайте
Две формулы логики предикатов Две формулы логики предикатов Очевидно, что все формулы равносильности алгебры высказываний будут верны, если в них вместо переменных подставить формулы логики предикатов. Но, кроме того, имеют место равносильности самой логики предикатов: Закон де Моргана: 1. 2. Закон двойного отрицания: 3. 4. 5. 6. 7. Для произвольного высказывания 8. 9. 10. 11. 12. 13. Формулы замены переменных (где 14. 15.
Формула предиката имеет нормальную форму, если она содержит только операции конъюнкции, дизъюнкции, и кванторные операции, а операция отрицания отнесена к элементарному предикату.
ПРИМЕР
Пусть дан предикат
Предварённой нормальной формой предиката называется такая нормальная форма предиката, в которой кванторные операторы либо отсутствуют, либо используются после операций алгебры логики.
ПРИМЕР Привести предикат из предыдущего примера к предваренной нормальной форме предиката
ТЕОРИЯ ГРАФОВ Начало теории графов как математической дисциплине было положено Леонардом Эйлером в его знаменитом решении задачи о Кенигсбергских мостах в 1736 году. План города Кенигсберга представлен на рис. 3.1. Задача о Кенигсбергских мостах сводилась к тому, чтобы построить маршрут своей воскресной прогулки так, чтобы, начиная в любой точке суши (A, B, C или D) пройти по всем мостам строго по одному разу и вернуться в исходную точку (начало маршрута).
A
B Рис. 3.1. Иллюстрация к задаче о Кенигсбергских мостах.
Такую задачу не предоставляется возможным решить классическими методами математики. Для решения такой задачи был предложен качественно новый аппарат – аппарат теории графов.
Основные понятия теории графов Графом называется пара следующего вида:
где
Иными словами, граф представляет совокупность множества вершин и дуг.
Рис. 3.2. Граф Граф, представленный на рис. 3. 2, состоит из множества вершин Графическое изображение графа является самым наглядным, но не единственным способом задания графа. Кроме того граф может быть задан: 1. перечислением:
2. множеством образов:
где Матрицей инцидентности Матрица инцидентности - это матрица вершин и инцидентных им дуг. Дуга инцидентна вершине, если эта дуга исходит или заходит в данную вершину. Вершина инцидентна дуге, если в эту вершину заходит или исходит данная дуга. В матрице инцидентности в первом столбце расположены вершины, в первой строке – дуги. Остальные ячейки матрицы инцидентности заполняются по следующему правилу: · · · · Для графа, представленного на рис. 3.2 матрица инцидентности имеет вид:
На практике в матрице инцидентности иногда нули не проставляются для наглядности.
Свойство матрицы инцидентности – сумма элементов по столбцам равна 0 или 2. Матрицей смежности Смежные дуги – это дуги инцидентные одной вершине. Смежные вершины – вершины, инцидентные одной дуге. Матрица смежности - это матрица смежных вершин. Матрица смежности заполняется по следующему правилу: Для графа, представленного на рис. 3.2 матрица смежности имеет вид:
Полустепенью захода Полустепенью исхода Степенью i-той вершины исхода
Свойства матрицы смежности: 1. Сумма единиц по строке определяет полустепень исхода; 2. Сумма единиц по столбцу определяет полустепень захода; 3. Сумма единиц по строкам и по столбцам определяет степень вершин. Основное свойство графа: В любых графах число вершин с нечетной степенью четно. Путем в графе называется последовательность дуг такая, что каждая следующая дуга исходит из вершины, в которую заходит предыдущая дуга. Длиной пути называется количество пройденных дуг. Простой путь – это такой путь, в котором дуга встречается не более одного раза. Элементарный путь – это путь, в котором вершина встречается не более одного раза. Контур – путь, начинающийся и заканчивающийся в одной точке. Петля – контур длиной в одну единицу. Графы бывают двух видов: · ориентированный граф (орграф) - это граф, состоящий из вершин и дуг. · неориентированный граф – это граф, состоящий из вершин и ребер. Ребро – это дуга, не имеющая направление.
Рис. 3.3. Неориентированный граф
В неориентированном графе путь называется цепью; контур – циклом. Неориентированный граф также может быть задан с помощью матриц инцидентности и смежности. Матрица инцидентности для неориентированного графа составляется по правилу: · · · Для графа, представленного на рис. 3.3, матрица инцидентности имеет вид:
Матрица смежности для неориентированного графа составляется по правилу: Для графа, представленного на рис. 3.3, матрица смежности имеет вид: Матрица смежности для неориентированного графа симметрична относительно главной диагонали. Степень i- той вершины равна сумме элементов по строке или по столбцу матрицы смежности.
Если в графе присутствуют как ребра, так и дуги, то он называется смешанным. Если между двумя вершинами существует более чем 1 дуга или ребро, то такой граф называется мультиграфом.
Рис. 3.4. Смешанный мультиграф.
Граф называется связным, если между любыми двумя вершинами которого существует путь (цепь).
Эйлеров граф. Эйлеровой цепью называется цепь, проходящая по всем ребрам графа. Эйлеровым циклом называется эйлеровая цепь, начинающаяся и заканчивающаяся в одной вершине. Эйлеровым графом называется граф, содержащий Эйлеров цикл.
ТЕОРЕМА: Для того чтобы связанный граф был Эйлеровым, необходимо и достаточно, чтобы степени всех вершин были четны
Данная теорема позволяет решить задачу о Кенигсбергских мостах. Граф, соответствующий данной задаче, имеет вид
А
С D
B Рис. 3.5 Граф «Кенигсбергские мосты»
Вершины графа (A, B, C, D) имеют степени:
Тогда в соответствии с теоремой Эйлера данный граф не является Эйлеровым. А это означает, что нельзя обойти все мосты г. Кенигсберга строго по одному разу, начав и закончив путь в одной точке суши.
Следствие из ТЕОРЕМЫ: Для того чтобы граф содержал Эйлеровую цепь, необходимо и достаточно, чтобы две вершины имели нечетную степень. При этом в одной из вершин цепь будет начинаться, в другой – заканчиваться.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 316; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.159.237 (0.009 с.) |

 и
и 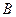 называются равносильными на области
называются равносильными на области  , если они принимают одинаковые логические значения при всех значениях входящих в них переменных, отнесенных к области
, если они принимают одинаковые логические значения при всех значениях входящих в них переменных, отнесенных к области 




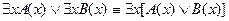

 (предиката, не связанного по переменной
(предиката, не связанного по переменной 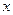 ) справедливы следующие формулы равносильности:
) справедливы следующие формулы равносильности:





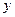 из одной предметной области):
из одной предметной области):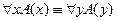

 Предваренная нормальная форма предиката
Предваренная нормальная форма предиката . Привести данный предикат к нормальной форме
. Привести данный предикат к нормальной форме
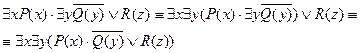

 , (3.1)
, (3.1) - график
- график  ;
; - множество вершин.
- множество вершин.



 ,
, - образ вершины
- образ вершины  - множество вершин, в которые исходят дуги из данной вершины.
- множество вершин, в которые исходят дуги из данной вершины. , если из i-той вершины исходит j-тая дуга:
, если из i-той вершины исходит j-тая дуга: , если в i-той вершину заходит j-тая дуга;
, если в i-той вершину заходит j-тая дуга; , если i-тая вершина не инцидента j-той дуге;
, если i-тая вершина не инцидента j-той дуге;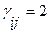 , если из i-той вершины исходит j-тая дуга и в нее же заходит, т.е. в i-той вершине j-тая дуга образует петлю.
, если из i-той вершины исходит j-тая дуга и в нее же заходит, т.е. в i-той вершине j-тая дуга образует петлю.

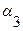

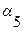

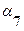


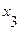



 , если из i-той вершины исходит дуга в j – тую вершину; во всех остальных случаях
, если из i-той вершины исходит дуга в j – тую вершину; во всех остальных случаях  i–той вершины называется число дуг, заходящих в данную вершину.
i–той вершины называется число дуг, заходящих в данную вершину. i-той вершины называется число дуг, исходящих из данной вершины.
i-той вершины называется число дуг, исходящих из данной вершины. называется сумма полустепеней захода и исхода:
называется сумма полустепеней захода и исхода: (3.2)
(3.2)


 (3.3)
(3.3)


