
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Различные формы представления высказыванийСодержание книги
Поиск на нашем сайте
Литерой - называется элемент высказывания x или её отрицание. Элементарной дизъюнкцией называется выражение следующего вида:
где Элементарной конъюнкцией называется выражение следующего вида:
Дизъюнктивной нормальной формой (ДНФ) формулы
где
Конъюнктивной нормальной формой (КНФ) формулы
где Любую формулу можно представить в виде ДНФ или КНФ.
ПРИМЕР Пусть дана формула
Требуется получить ДНФ и КНФ данной формулы. Применяя формулы равносильности, получаем КНФ
Применяя формулы равносильности, получаем ДНФ
Совершеннойдизъюнктивной нормальной формой(СДНФ) формулы 1. Все элементарные конъюнкции, входящие в ДНФ 2. Все элементарные конъюнкции, входящие в ДНФ 3. Каждая элементарная конъюнкция, входящая в ДНФ 4. Каждая элементарная конъюнкция, входящая в ДНФ СДНФ 1. по таблице истинности; 2. с помощью равносильных преобразований. Первый способ получения СДНФ С помощью равносильных преобразований формулы 1. Элементарная конъюнкция
2. Если в ДНФ
одну элементарную конъюнкцию можно отбросить. 3. Если элементарная конъюнкция
эту элементарную конъюнкцию можно отбросить 4. Если элементарная конъюнкция
одну переменную СДНФ формулы
ПРИМЕР Получить СДНФ формулы С помощью равносильных преобразований получаем СДНФ
С помощью таблицы истинности получаем СДНФ
СДНФ Очевидно, что в результат двух способов совпадает.
Совершеннойконъюнктивной нормальной формой(СКНФ) формулы 1. Все элементарные дизъюнкции, входящие в КНФ 2. Все элементарные дизъюнкции, входящие в КНФ 3. Каждая элементарная дизъюнкция, входящая в КНФ 4. Каждая элементарная дизъюнкция, входящая в КНФ СКНФ 1. по таблице истинности; 2. с помощью равносильных преобразований. По первому способу по таблице истинности получаем СДНФ
С помощью равносильных преобразований формулы 1. Элементарная дизъюнкция
2. Если в КНФ
одну элементарную дизъюнкцию можно отбросить. 3. Если элементарная дизъюнкция
эту элементарную дизъюнкцию можно отбросить. 4. Если элементарная дизъюнкция
одну переменную СКНФ формулы
ПРИМЕР Получить СКНФ формулы С помощью равносильных преобразований получаем СКНФ
С помощью таблицы истинности получаем СДНФ
Очевидно, что в результат двух способов совпадает.
СДНФ формулы
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 252; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.150.86 (0.009 с.) |

 , (2.2)
, (2.2) - литера.
- литера.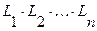 , (2.3)
, (2.3) называется выражение вида:
называется выражение вида: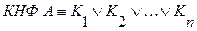 , (2.4)
, (2.4) - элементарная конъюнкция.
- элементарная конъюнкция.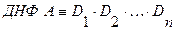 , (2.5)
, (2.5) - элементарная дизъюнкция.
- элементарная дизъюнкция.


 ДНФ
ДНФ  , тогда используются следующие равносильные преобразования:
, тогда используются следующие равносильные преобразования:
 ,
, ,
, ,
,

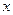
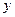
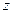
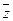
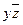

 , а СКНФ
, а СКНФ 

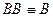 ,
, ,
, ,
,






