Подання графа списком пар (списком ребер)

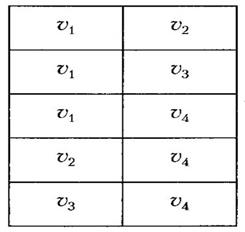
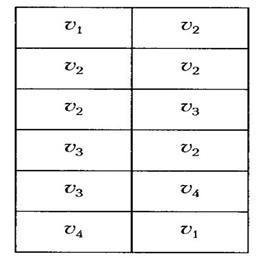
Метод зображення графа списком пар, які відповідають його ребрам (або дугам), значно економніший щодо пам'яті, особливо якщо т (кількість ребер) значно менша, ніж п² (п — кількість вершин). Пара [и, v] відповідає ребру {и, v}, якщо граф неорієнтований, і дузі (и, v), якщо граф орієнтований. Для графів, зображених на рис. 3.14 та 3.15, списки пар подані відповідно на рис. 3.16, а та 3.16, б.

Рис. 3.15 Матриця суміжності неорієнтованого графу

Рис. 3.16. Матриця суміжності орієнтованого графу

 

Очевидно, що обсяг пам'яті в цьому разі дорівнює 2т (т — кількість ребер або дуг). Це найекономніший щодо пам'яті спосіб. Його вада — велика (порядку п_і) кількість кроків для знаходження множини вершин, до яких ідуть ребра чи дуги із заданої вершини. Ситуацію можна значно поліпшити, упорядкувавши множину пар лексикографічно та застосувавши двійковий пошук.

 

Подання графа списками суміжності

Орієнтований граф G (без кратних дуг, але, можливо, з петлями) можна подати, зазначивши скінченну не порожню множину вершин V та відповідність Г, котра показує, як зв'язані між собою вершини. Відповідність Г — багатозначне відображення множини V у V. Граф у такому разі позначають парою G = (V, Г). У літературі часто означають (орієнтований) граф саме в таких поняттях [19, 20].

Ейлерів цикл у графі

Початок теорії графів як розділу математики пов’язують із задачею про кенінгсберські мости. Сім мостів міста Кенігсберга (нині Калінінград у Росії) було розміщено на річці Прегель так, як зображено на рис 3.30. Чи можна починаючи з якоїсь точки міста, пройти через усі мости точно по одному разу й повернутися у початкову точку? Швейцарський математик Л. Ейлер розв’язав цю задачу. Його розв’язання опубліковано 1736 р., було першим явним застосування теорії графів. Ейлер поставив у відповідність плану міста мультиграф G, вершини якого відповідають чотирьом частинам A, B, C, D міста, а ребра мостам. Цей граф зображено на рис. 3.31.

 

Рис 3.30. Кенігсбергські мости та їх модель за допомогою графу

Рис 3.30. Модель кенігсбергських мостів за допомогою графу

 

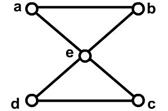
Отже, задачу про кенінгсберські мости мовою теорії графів можна сформулювати так: чи існує в мультиграфі G простий цикл, який містить усі ребра цього мультиграфа? Ейлер довів нерозв’язність задачі про кенінгсберські мости. Нагадуємо, що в простому циклі ребра не повторюються, а вершини можуть повторюватись.

Ейлеровим циклом у зв’язному мультографі G називають простий цикл, який містить усі ребра графа, ейлеревим шляхом – простий шлях, що містить усі ребра графа.

Приклад 3.31. На рис. 3.32 проілюстровано концепцію ейлеревих циклів і шляхів. Граф G1 має ейлерів цикл, наприклад, a, e, c, d, e, b, a; граф G3 не має ейлеревого циклу, але має ейлерів шлях: a, c, d, e, b, d, a, b; граф G2 не має ні ейлеревого циклу, ні ейлеревого шляху.

Існує простий критерій (необхідна й достатня умова) для виявлення того, чи має граф ейлерів цикл.

ТЕОРЕМА 3.10. Зв’язний граф G має ейлерів цикл тоді й лише тоді, коли степені всіх його вершин парні.

Доведення. Необхідність. Нехай у графі G існує ейлерів цикл. Тоді він проходить через кожну вершину графа і входить до неї по одному ребру, а виходить по іншому. Це означає, що кожна вершина інцидентна парній кількості ребер ейлеревого циклу. Оскільки такий цикл містить усі ребра графа G, то звідси випливає парність степенів усіх його вершин.

Достатність. Припустимо тепер, що всі вершини графа G мають парний степінь почнемо шлях Р₁ із довільної вершини V₁ і продовжемо його наскільки це можливо, вибираючи щоразу нове ребро. Позаяк степені усіх вершин парні, то, увійшовши у будь-яку вершину, відмінну від V₁, ми завжди маємо можливість вийти з неї через іще не пройдене ребро. Тому шлях Р₁ можна продовжити додавши це ребро. Отже, побудова шляху Р₁ завершиться у вершині V₁, тобто Р₁ обов’язково виявиться циклом. Якщо з’ясується що шлях Р₁ містить усі ребра графа G, то це ейлерів цикл. У протилежному випадку вилучемо з G всі ребра типу Р₁ і всі вершини, інцидентні лише вилученим ребрам. Отримаємо якийсь зв’язний граф G₁. Оскільки Р₁ та G мають вершини лише парних степенів,то, очевидно, і граф G₁ матиме цю властивість. Окрім того, позаяк граф G зв’язний, то графи Р₁ та G₁ мають принаймні одну спільну вершину V₂. Тепер із вершини V₂ побудуємо цикл Р₁ в графі G₁ аналогічно до того, як ми будували цикл Р₁ у графі G. Цикл Р₁ на місце вершини V₂. Одержимо цикл Р₃. Описані побудови показано на рис.3.33

Рис 3.30. Алгоритм Фльорі

Цикл Р₁ = v₁, v₄, v₃, P₂, v₁ = v₁, v₄, v₃, v₂, v₅, v₆, v₂, v₁ ейлерів. Якби він виявився не ейлеревим, то потрібно продовжити аналогічні побудови і отримати ще більший цикл. Цей процес закінчиться побудовою ейлеревого циклу. Зазначимо, що доведення достатності має конструктивний характер: подано алгоритм побудови ейлеревого циклу.

Існує і інший алгоритм побудови ейлерового циклу, який дає змогу побудувати цей цикл одразу. Це алгоритм Флері (Fleury).