
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм Флері побудови ейлерового циклуСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Робота алгоритму полягає в нумерації ребер к процесі побудови ейлеревого циклу. Крок 1. Початок. Починаємо з довільної вершини u та присвоюємо довільному ребру {u,v} номер 1. Викреслюємо ребро {u,v} й переходимо у вершину v. Крок 2. Ітерація. Нехай v – вершина, у яку ми перейшли на попередньому кроці, k - останні присвоєний номер. Вибираємо довільне ребро, інцидентне вершині v, причому міст вибираємо лише тоді, коли немає інших можливостей. Присвоюємо вибраному ребру номер (k+1) і викреслюємо його. Крок 3. Закінчення. Цей процес закінчуємо, коли всі ребра графа викреслено та пронумеровано – ці номери задають послідовність ребер в ейлеревому циклі. Повертаючись до задачі про кенінгсберські мости, виявляємо, що мультограф, зображений на рис. 3.31, має всі вершини непарного степеня, отже цей мультиграф не має ейлерового циклу, тому неможливо пройти кожний міст по одному разу й повернутися у початкову точку шляху. ТЕОРЕМА 3.11. Зв’язний мультиграф має ейлерів шлях, але не має ейлерового циклу тоді і лише тоді, коли він має точно дві вершини непарного степеня. Зазначимо, що будь-який ейлерів шлях починається в одній із цих двох вершин непарного степеня, а закінчується в іншій. Оскільки мультиграф для кенінгсберських мостів має чотири вершини з непарними степенями, можна дійти висновку про неможливість пройти кожен міст по одному разу, навіть якщо не потрібно вертатись у початкову точку. Граф, який має ейлерів цикл, часто називають ейлеревим. Ейлеровим циклом у слабко зв’язному орієнтованому мультографі називають орієнтований простий цикл, який містить усі ребра графа. ТЕОРЕМА 3.12. Орієнтований слабко зв’язний мультиграф має ейлерів цикл тоді й лише тоді, коли напівстепінь входу кожної вершини дорівнює її напівстепеню виходу. Гамільтонів цикл у графі Шлях x0,x1,…,xn-1,xn у зв’язному графі G = (V, E) називають гамільтоновим шляхом, якщо V = { x0,x1,…,xn-1,xn } і Цикл x0,x1,…,xn-1,xn, x0 (тут n>1) у графі G = (V, E) називають гамільтоновим циклом, якщо x0,x1,…,xn-1,xn, - гамільтонів шлях. Інакше кажучи, гамільтонів цикл і гамільтонів шлях проходять через кожну вершину графа точно один раз (можливо, окрім першої й останньої вершин). Зазначимо, що гамільтонові цикл і шлях, узагалі кажучи, не містять усіх ребер графа. Термін «гамільтонів» у цих означеннях походить від імені відомого ірландського математика У. Гамільтона (W. Hamilton), який 1857 р. запропонував гру «Навколосвітня подорож». Кожній із двадцяти вершин додекаедра (правильного дванадцятигранника, грані якого – п’ятикутники) прописано назву одного з великих міст світу. Потрібно, розпочавши з довільного міста, відвідати решту 19 міст точно один раз і повернутися у початкове місто. Перехід дозволено ребрами додекаедра [52]. Приклад 3.32. Ту саму задачу можна зобразити й на площині (рис. 3.34). Вона зводиться до відшукання в графі гамільтонового циклу. Один із можливих розв’язків показано пунктирними лініями.
Рис 3.31. Розв’язок задачі про всесвітню подорож
Не всі зв’язні графи мають гамільтонів цикл хоча б тому, що такий граф має бути двозв’язним (тобто граф, який має точки з’єднання, не може мати гамільтонового циклу). Приклад графа зображеного на рис. 3.35, свідчить, що двозязності недостатньо для наявності гамільтонового циклу. Незважаючи на зовнішню подібність формулювань задач про існування ейлерового й гамільтонового циклів, ці задачі принципово різні. Використовуючи результати попереднього підрозділу, легко виявити, чи має граф ейлерів цикл, і, якщо має, то побудувати його.
Рис 3.31. Двозв’язний граф, який не має гамільтонового циклу
Ситуація для гамільтонового циклу істотно інша. Відповісти на питання, чи має граф гамільтонів цикл, зазвичай, дуже важко. Вивчення достатніх умов наявності в графі гамільтонового циклу – один із важливих напрямів у теорії графів. Інтуїтивно зрозуміло, що граф із багатьма ребрами, достатньо рівномірно розподіленими, з великою ймовірністю має гамільтонів цикл. Доведемо одну теорему з теорем такого типу. ТЕОРЕМА 3.13 (Г. Дірака, 1952 р.). Якщо для кожної вершини v зв’язного простого графа з n>=3 вершинами виконується нерівність deg(v)>=n/2, то цей граф має гамільтонів цикл. Як знайти гамільтонів цикл або переконатися, що його немає? Очевидний алгоритм, який можна застосувати, - це повний перебір усіх можливостей, тобто n! перестановок усіх вершин графа й перевірок. Зрозуміло що такий спосіб не практичний. Розгляд реального алгоритму бектрекінг відкладемо до наступного розділу (розділ 4.5, приклад 4.15). Для задачі знаходження гамільтонового невідомий ефективний (тобто з поліноміальною складністю) алгоритм розв’язання, і є вагомі підстави вважати, що його не існує. Граф, який містить гамільтонів цикл, часто називають гамільтоновим графом.
|
||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 937; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.01 с.) |

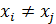 для
для  .
.




