Пошук ушир у простому зв'язному графі

У процесі пошуку вшир вершини графа проглядають в іншій послідовності, ніж у методі пошуку вглиб, і їм надають BFS - номери (від англ. breadth first search). BFS - номер вершини х позначають BFS(x). Під час пошуку рухаються вшир, а не вглиб: спочатку проглядають усі сусідні вершини, після цього — сусіди сусідів і так далі.

У ході реалізації алгоритму використовують структуру даних для збереження множин, яку називають чергою (англ. queue). Із черги можна вилучити тільки той елемент, який перебував у ній найдовше: працює принцип «першим прийшов — першим вийшов» (first in, first out — скорочено FIFO). Елемент включається у хвіст черги, а виключається з її голови. Пошук ушир, узагалі кажучи, відрізняється від пошуку вглиб заміною стеку на чергу. Після такої модифікації що раніше відвідується вершина (включається в чергу), то раніше вона використовується (і виключається з черги). Використання вершини полягає в перегляді одразу всіх іще не відвіданих її сусідів. Усю процедуру подано нижче.

 

Алгоритм пошуку вшир у простому зв'язному графі

Наведемо кроки алгоритму.

Крок 1. Почати з довільної вершини v_s. Виконати BFS(v_s):= 1. Включити вершину v_s у чергу.

Крок 2. Розглянути вершину, яка перебуває на початку черги; нехай це буде вершина х. Якщо для всіх вершин, суміжних із вершиною х, уже визначено BFS - номери, то перейти до кроку 4, інакше — до кроку 3.

Крок 3. Нехай {х, у} — ребро, у якому номер BFS(y) не визначено. Позначити це ребро потовщеною суцільною лінією, визначити BFS(y) як черговий BFS - номер, включити вершину у у чергу й перейти до кроку 2.

Крок 4. Виключити вершину х із черги. Якщо черга порожня, то зупинитись, інакше — перейти до кроку 2.

 

Щоб результат виконання алгоритму був однозначним, вершини, які суміжні з вершиною х, аналізують за зростанням їх порядкових номерів (або в алфавітному порядку). Динаміку роботи алгоритму пошуку вшир також зручно відображати за допомогою протоколу обходу. Він аналогічний попередньому й відрізняється лише третім стовпцем: тепер це — уміст черги (уважаємо, що голова черги ліворуч, а хвіст — праворуч).

 

Приклад 3.36. Виконаємо обхід графа на рис. 3.39 пошуком ушир, починаючи з вершини b. Розв'язок зображено на рис. 3.41, протокол пошуку вшир подано в табл. 3.6.

Таблиця 3.6

Вершина	BFS-номер	Вміст черги
B		b
C		be
D		bed
-	-	cd
F		cdf
G		cdfg
H		cdfgh
-	-	dfgh
А		dfgha
-	-	fgha
Е		fghae
-	-	ghae
-	-	hae
-	-	ae
-	-	e
-	-

 

У процесі роботи наведених алгоритмів будується дерево Т пошуку відповідно вглиб і вшир — на рис. 3.40 і 3.41 його виділено потовщеними лініями (див. розділ 4).

Обчислювальна складність обох алгоритмів обходу однакова й у разі подання графа списками суміжності становить 0(m + n), де m — кількість ребер, а п — кількість вершин графа.

 

Планарні графи

Розглянемо неорієнтовані графи. Часто не має значення, як зобразити граф на рисунку, бо ізоморфні графи несуть одну й ту саму інформацію. Проте інколи важливо, чи можна подати граф на площині так, щоб його зображення задовольняло певним вимогам. Наприклад, у радіоелектроніці в процесі виготовлення мікросхем друкованим способом електричні ланцюги наносять на плоску поверхню ізоляційного матеріалу. Оскільки провідники не ізольовані, то вони не мають перетинатись. Аналогічна задача виникає під час проектування залізничних та інших шляхів, де переїзди небажані. Так виникає поняття плоского графа. Плоским називають граф, зображений на площині так, що ніякі два його ребра геометрично не перетинаються ніде, окрім інцидентних їм вершин. Граф, ізоморфний до плоского графа, називають планарним.

Приклад 3.37. Усі три графи на рис. 3.42 планарні, але лише другий і третій із них плоскі.

Рис. 3.42

 

Плоский граф розбиває площину на області, одна з яких необмежена. їх називають гранями плоского графа; необмежену область називають зовнішньою гранню.

Приклад 3.38. На рис. 3.43 зображено плоский граф. Він має чотири грані: r₁, r₂, r₃, r₄; грань r₄ зовнішня.

 

Рис. 3.43

 

ТЕОРЕМА 3.14 (Ейлера про плоскі графи). Нехай зв'язний плоский граф G має п вершин, т ребер і r граней. Тоді п + r = т + 2.

Доведення. Проводимо індукцією за кількістю ребер у графі G. Якщо т = 0, то п = 1, r = 1, і теорема справджується. Допустимо, що теорема справджується для довільного плоского графа G, який має т- 1 ребро, і додамо до G нове ребро e. Можливі три випадки.

1. Ребро e — петля; тоді виникне нова грань, а кількість вершин залишитьсянезмінною.

2. Ребро e з'єднує дві різні вершини графа С; у такому разі одна з граней розпадеться на дві, тому кількість граней збільшиться на одну, а кількість вершин не зміниться.

3. Ребро e інцидентне лише одній вершині в С; тоді потрібно додати ще одну вершину; отже, кількість вершин збільшиться на одну, а кількість граней не зміниться.

Твердження теореми залишається правильним у кожному з цих випадків. Оскільки інші випадки неможливі, то індукцію завершено й теорему доведено.

ТЕОРЕМА 3.15. Графи К₅ і К_3,3 не планарні.

Доведення. Граф К₅ має п'ять вершин і десять ребер (див. рис. 3.9). Припустимо, що він планарний; тоді існує ізоморфний до нього плоский граф. За теоремою Ейлера r = m + 2 - п = 10 + 2 - 5 = 7. Зазначимо, що будь-яке ребро плоского графа або розділяє дві різні грані, або являє собою міст. Позаяк граф К₅ не має петель і кратних ребер, то кожна грань обмежена принаймні трьома ребрами. Тому число Зr - оцінка знизу подвоєної кількості ребер графа, тобто Зr < 2т, звідки випливає, що 21 20. Суперечність.

У графі К_3,3 кількість вершин п = 6, а кількість ребер т = 9 (див. рис. 3.10). Припустимо, що він планарний. Тоді в ізоморфному до нього плоскому графі за теоремою Ейлера кількість граней r = т + 2 - п = 9 + 2 - 6 = 5. Будь-яка грань дводольного графа має бути обмежена принаймні чотирма ребрами. Отже, 4 × r 2 × m, звідки випливає, що 10 < 9. Суперечність.

Два графи називаються гомеоморфними, якщо їх можна отримати з одного графа додаванням до його ребер нових вершин степеня 2 (рис. 3.44).

 

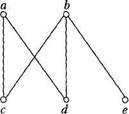
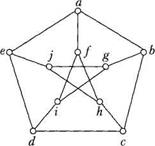
Наступна теорема дає критерій (необхідну й достатню умову) планарності графа.

ТЕОРЕМА 3.16 (Куратовського). Граф планарний тоді й лише тоді, коли він не містить підграфів, гомеоморфних графам К₅ або К_{3, 3}.

Необхідність умов теореми вже доведено, бо доведено непланарність графів К₅ і К_3,3, а доведення достатності складне, і ми його не наводимо.

Приклад 3.39. На рисунку 3.45 зображено граф Петерсена, а на рис 3.46 — його підграф, гомеоморфний К_{3, 3}. Отже, за теоремою Куратовського, граф Петерсена непланарний.

Рис. 3.45

Рис. 3.46

Окрім теореми Куратовського є й інші критерії планарності графів. Практично перевірити умови, якими характеризуються планарні графи, не завжди просто. Проте розроблено ефективні алгоритми, які дають змогу для будь-якого заданого графа знайти його зображення на площині без перетину ребер або переконатись, що це неможливо (якщо граф непланарний).