
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зважені графи й алгоритми пошуку найкоротших шляхівСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
У реальних задачах на графах часто потрібно брати до уваги додаткову інформацію – фактичну віддаль між окремим пунктами, вартість проїзду, час проїзду тощо. Для цього використовують поняття зваженого графа. Зваженим називають простий граф, кожному ребру е якого приписано дійсне число w(e). Це число називають вагою ребра е. Аналогічно означають зважений орієнтований граф: це такий орієнтований граф, кожній дузі е якого приписано дійсне число w(e) називане вагою дуги. Розглянемо три способи зберігання зваженого графа G = (V, E) в пам’яті комп’ютера. Нехай |V | = n, |E | = m. Перший – подання графа матрицею ваг W, яка являє собою аналог матриці суміжності. Її елемент wij = w(vi, vj), якщо ребро {vi, vj} є Е (у разі орієнтованого графа дуга (vi, vj) є Е). Якщо ж ребро {vi, vj}!є Е (або дуга (vi, vj)!є Е), то wij = 0, чи Wij = Другий спосіб - подання графа списком ребер. Для зваженого графа від кожний елемент списку Е можна відвести три комірки – дві для ребра й одну для його ваги, тобто всього потрібно 3m комірок. Третій спосіб – подання графа списками суміжності. Для зваженого графа кожний список Adj[u] містить окрім покажчиків на всі вершини v Г(u) ще й числа w(u, v). Довжиною шляху у зваженому графі називають суму ваг ребер (дуг), які утворюють цей шлях. Якщо граф не зважений, то вагу кожного ребра (кожної дуги) уважають рівною 1 й отримують раніше введене поняття довжини шляху як кількості ребер (дуг) у ньому. Задача про найкоротший шлях полягаю в знаходженні найкоротшого шляху від заданої початкової вершини a до заданої вершини z. Наступні дві задачі – безпосередні узагальнення сформульованої задачі про найкоротший шлях. 1. Для заданої початкової вершини a знайти найкоротші шляхи від a до всіх інших вершин. 2. Знайти найкоротші шляхи між усіма парами вершин. Виявляється, що майже всі методи розв’язання задачі про найкоротший шлях від заданої початкової вершини a до заданої вершини z також дають змогу знайти найкоротші шляхи від a до всіх інших вершин графа. Отже, за їх допомогою можна розв’язати задачу 1 із невеликими додатковими обчислювальними витратами. З іншого боку, задачу 2 можна розв’язати n разів застосувавши алгоритм задачі 1 із різними початковими вершинами, або один раз застосувавши спеціальний алгоритм.
Розглянемо два алгоритми: перший алгоритм призначений для розв’язування задачі 1, другий – для задачі 2. Найефективніший алгоритм визначення довжини найкоротшого шляху від фіксованої вершини до будь-якої іншої запропонував у 1959 р. датський математик Е. Дейкстра (E. Dijkstra). Цей алгоритм застосований лише тоді, коли вага кожного ребра (дуги) додатна. Опишемо докладно цей алгоритм для орієнтованого графа. Нехай G = (V,E) – зважений орієнтований граф, w(vi,vj) – вага дуги (vi,vj). Почавши з вершини a, знаходимо віддаль від a до кожної із суміжних з нею вершин. Вибираємо вершину, віддаль якої до вершини a найменша; нехай це буде вершина v* вздовж шляху, який проходить через вершину v*. Якщо для якоїсь із таких вершин ця віддаль менша від поточної, то заміняємо нею поточну віддаль. Знову вибираємо вершину, найближчу до a й не вибрану раніше; повторюємо процес. Описаний процес зручно виконувати за допомогою присвоювання вершинам міток. Є мітки двох типів – тимчасові та постійні. Вершини з постійними мітками групують у множину М, яку називають множиною позначених вершин. Решта вершин має тимчасові мітки, і множину таких вершин позначимо як T, T = V\M. Позначатимемо мітку (тимчасову чи постійну) вершини v як l(v). Значення постійної мітки l(v) дорівнює довжині найкоротшого шляху, який проходить лише через вершини з постійними мітками. Фіксованою початковою вершиною вважаємо вершину a; довжину найкоротшого шляху шукаємо до вершини z (або до всіх вершин графа). Тепер формально опишемо алгоритм Дейкстри. Алгоритм Дейкстри Наведемо кроки алгоритму. Крок 1. Присвоювання початкових значень. Виконати l(a):=0 та вважати цю мітку постійною. Виконати l(v):= Крок 2. Оновлення міток. Для кожної вершини v є Г(x)\M замінити мітки: l(v):= min{l(v); l(x)+w(x,v)}, тобто оновлювати тимчасові мітки вершин, у які з вершини x іде дуга. Крок 3. Перетворення мітки в постійну. Серед усіх вершин із тимчасовими мітками знайти вершину з мінімальною міткою, тобто знайти вершину v* з умови l(v*) = min{l(v)}, v є T, де T = V\M. Крок 4. Уважати мітку вершини v* постійною і виконати M:=MÈ{v*}; x:=v* (вершину v* включено в множину М). Крок 5. а) Для пошуку шляху від a до z; якщо x = z, то l(z) – довжина найкоротшого шляху від a до z; зупинитись; якщо x!=z, то перейти до кроку 2.
б) Для пошуку шляхів від a до всіх інших вершин: якщо всі вершини отримали постійні мітки (включені в множину М) то ці мітки дорівнюють довжинам найкоротших шляхів, зупинитися; якщо деякі вершини мають тимчасові мітки, то перейти до кроку 2.
|
||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 1347; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.63.214 (0.01 с.) |

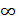 залежно від розв’язуваної задачі.
залежно від розв’язуваної задачі. для всіх v!=a вважати ці мітки тимчасовими. Виконати x:=a, M:={a}.
для всіх v!=a вважати ці мітки тимчасовими. Виконати x:=a, M:={a}.


